NURBS
B-splines racionales no uniformes o NURBS (acrónimo inglés de non-uniform rational B-spline) es un modelo matemático muy utilizado en la computación gráfica para generar representando curvas y superficies.

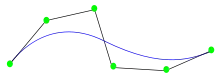
Versión animada
Historia
El desarrollo de NURBS empezó en 1950 por ingenieros que necesitaban la representación matemática precisa de superficies de forma libre como las usadas en carrocerías de automóviles, superficies de exteriores aeroespaciales y cascos de barcos, que pudieran ser reproducidos exacta y técnicamente en cualquier momento. Las anteriores representaciones de este tipo de diseños solo podían hacerse con modelos físicos o maquetas realizadas por el diseñador o ingeniero.
Los pioneros en esta investigación fueron Pierre Bézier quien trabajaba como ingeniero en Renault, y Paul de Casteljau quien trabajaba en Citroën, ambos en Francia. Bézier y Casteljau trabajaron casi en paralelo, aunque ninguno de los dos conoció el trabajo que el otro desarrollaba. Bezier publicó primero sus trabajos y por esta razón tradicionalmente se le ha asociado a las Bézier-Splines (splines de Bézier, que son representadas con puntos de control describiendo a la curva misma), mientras que el nombre de Casteljau solo es conocido por los algoritmos que desarrolló para la evaluación de superficies paramétricas. En la década de 1960 se desarrollaron las NURBS, y se convirtieron en la generalización de las Bézier splines.
Las primeras NURBS fueron usadas en paquetes propietarios de diseño asistido por computadora de las compañías automotrices. Posteriormente formaron parte del estándar en paquetes de gráficos por computadora. En 1985, el primer modelador interactivo de NURBS para PC, llamado Macsurf (posteriormente Maxsurf), fue desarrollado por Formation Design Systems, una pequeña compañía en Australia. Maxsurf es un sistema de diseño para cascos, que pretendía la creación de barcos, botes y yates, para los diseñadores quienes tenían la necesidad de alta precisión en el esculpido de superficies. Actualmente las aplicaciones más profesionales de gráficos por computadora para equipos de escritorio implementan la tecnología.
Especificaciones técnicas
Una curva NURBS se define por su grado, un conjunto de puntos de control ponderados, y un vector de nodos. Las curvas y superficies NURBS son generalizaciones de curvas B-splines y curvas de Bézier, así como de superficies, siendo su diferencia principal la ponderación de los puntos de control que hacen a las curvas NURBS racionales (las curvas B-splines racionales no uniformes son un caso especial de las curvas B-splines racionales). Mientras que las curvas de Bézier se desarrollan en una sola dirección paramétrica, normalmente llamada s o u, las superficies NURBS evolucionan en dos direcciones paramétricas, llamada s y t o u y v.

Mediante la evaluación de una curva de Bézier o una curva NURBS en diversos valores del parámetro, la curva se puede representar en un espacio Cartesiano de dos o tres dimensiones. Asimismo, mediante la evaluación de una superficie NURBS en diversos valores de los dos parámetros, la superficie se puede representar en el espacio cartesiano.
Las curvas y superficies NURBS son útiles por varias razones:
- Son invariantes bajo transformaciones afines,[1] así como de perspectiva:[2] operaciones de rotación y traslación se pueden emplear en las curvas y superficies NURBS aplicándolas a sus puntos de control.
- Ofrecen una estructura matemática común para figuras analíticas estándar (por ejemplo, cónicas) y figuras de forma libre.
- Proporcionan flexibilidad para diseñar una gran variedad de figuras.
- Reducen el consumo de memoria al almacenar figuras (en comparación con métodos más sencillos).
- Pueden ser evaluados rápidamente por algoritmos numéricamente estables y precisos.
En las siguientes secciones, las curvas NURBS se analizan en una dimensión. Debe tenerse en cuenta que todo esto se puede generalizar a dos o incluso más dimensiones.
Puntos de control
Los puntos de control determinan la forma de la curva. Generalmente, cada punto de la curva se calcula tomando la suma ponderada de una serie de puntos de control. El peso de cada punto varía de acuerdo con el parámetro que lo rige. Para obtener una curva de grado d, el peso de cualquier punto de control es diferente de cero solo en D +1 intervalos del espacio de parámetros. Dentro de estos intervalos, el peso cambia de acuerdo a una función polinómica (funciones de base) de grado d. En los límites de los intervalos, las funciones base se aproximan lentamente a cero, determinando esta velocidad con el grado del polinomio. Como ejemplo, la función base de grado uno es una función triangular. Incrementa desde cero a uno, después decrementa de nuevo a cero. Mientras se incrementa, la función base del punto de control anterior cae. De esta manera, la interpolación entre los dos puntos es una curva, y esta curva resultante es un polígono, que es continua, pero no diferenciable en los límites del intervalo, o los nodos. Polinomios de grado superior, en consecuencia, tienen más derivadas continuas. Se debe tener en cuenta que dentro del intervalo la naturaleza polinómica de las funciones base y la linealidad de la construcción hace a la curva perfectamente suave, por lo que es solo en los nodos que puede surgir discontinuidad.
El hecho de que un único punto de control solo influye en aquellos intervalos en los que es activa es una propiedad muy deseable, es conocido como apoyo local. En el modelado, esto permite el cambio de parte de una superficie, mientras las otras partes se mantienen igual.
Agregar más puntos de control permite una mejor aproximación a una curva dada, aunque solo cierta clase de curvas se puede representar exactamente con un número finito de puntos de control. Las curvas NURBS también cuentan con un peso escalar para cada punto de control. Esto permite mayor control sobre la forma de la curva sin aumentar indebidamente el número de puntos de control. En particular, se añaden secciones cónicas como círculos y elipses al conjunto de curvas que se pueden representar exactamente. El término racional en NURBS se refiere a estos pesos.
Los puntos de control pueden tener cualquier dimensión. Los puntos de una dimensión solo definen una función escalar del parámetro. Estos se utilizan normalmente en los programas de procesamiento de imagen para ajustar el brillo y las curvas de color. Los puntos de control tridimensionales se utilizan mucho en el modelado 3D, donde se emplean cotidianamente como referencia de la palabra "punto", un lugar en el espacio 3D. Los puntos multidimensionales pueden ser usados para controlar conjuntos de valores en base al tiempo, por ejemplo, los diferentes ajustes de posición y de rotación del brazo de un robot. Las superficies NURBS son solo una aplicación de esta. Cada "punto" de control es en realidad un vector lleno de puntos de control, definiendo una curva. Estas curvas comparten su grado y el número de puntos de control, y abarcan una dimensión del espacio de parámetros. Por interpolación de estos vectores de control sobre la otra dimensión del espacio de parámetros, un conjunto continuo de curvas es obtenido, definiendo la superficie.
Vector de nodos
El vector de nodos es una secuencia de valores de parámetros que determinan dónde y cómo los puntos de control afectar a la curva NURBS. El número de nodos es siempre igual al número de puntos de control más el grado de la curva más uno. El vector de nodos divide el espacio paramétrico en los intervalos mencionados antes, normalmente conocidos como segmentos de nodo. Cada vez que el valor del parámetro introduce un nuevo segmento de nodo, un nuevo punto de control se activa, mientras que un punto de control antiguo se descarta. De ello se deduce que los valores en el vector de nodos deben estar en orden ascendente, por lo que (0, 0, 1, 2, 3, 3) es válido, mientras que (0, 0, 2, 1, 3, 3) no lo es.
Nodos consecutivos pueden tener el mismo valor. Esto define entonces un segmento de nodo de longitud cero, lo que implica que dos puntos de control se activan al mismo tiempo (y, por supuesto, dos puntos de control antiguos se desactivarán). Esto tiene un impacto en la continuidad de la curva resultante o de sus derivadas más altas, por ejemplo, permite la creación de esquinas en una curva NURBS suavizada. Un número de nodos que coinciden se denomina a veces como un nodo con cierta multiplicidad. Nodos con multiplicidad dos o tres se conocen como nodos dobles o triples. La multiplicidad de un nodo se limita al grado de la curva, puesto que una multiplicidad mayor dividiría a la curva en partes inconexas y dejaría a los puntos de control sin usar. Para NURBS de primer grado, cada nodo se asocia a un punto de control.
El vector de nodos por lo general comienza con un nodo que tiene una multiplicidad igual a la orden. Esto tiene sentido, ya que activa los puntos de control que influyen en el primer segmento de nodo. Del mismo modo, el vector de nodos por lo general termina con un nodo de esa multiplicidad. Curvas con tales vectores de nodos inician y terminan en un punto de control.
Los valores individuales de los nodos no son significativos por sí mismos, solo importa la proporción de diferencia entre los valores de los nodos. Por lo tanto, los vectores de nodos (0, 0, 1, 2, 3, 3) y (0, 0, 2, 4, 6, 6) producen la misma curva. Los valores de las posiciones de los nodos influyen en el mapeo del espacio de parámetros al espacio de la curva. La renderización de una curva NURBS se hace generalmente en pasos con distancia fija a través del rango de parámetros. Mediante el cambio de las longitudes de los segmentos de nodo, se pueden utilizar más puntos de muestra en regiones donde la curvatura es máxima. Otro uso es en situaciones en las que el valor del parámetro tiene algún significado físico, por ejemplo, si el parámetro es el tiempo y la curva describe el movimiento del brazo de un robot. Las longitudes del segmento de nodo luego se traducen en velocidad y aceleración, que son esenciales para evitar daños al brazo robótico o su entorno. Esta flexibilidad en el mapeo es a lo que la frase no uniforme en NURBS se refiere.
Necesarios solo para los cálculos internos, los nodos generalmente no son útiles para los usuarios de modelado de software. Por lo tanto, muchas aplicaciones de modelado no hacen a los nodos editables o incluso visibles. Por lo general es posible establecer vectores de nodos razonables observando la variación en los puntos de control. Las versiones más recientes de software para NURBS (por ejemplo, Autodesk Maya y Rhinoceros 3D) permiten la edición interactiva de las posiciones de los nodos, pero esto es significativamente menos intuitivo que la edición de puntos de control.
Grado
El orden de una curva NURBS define el número de puntos de control cercanos que influyen en cualquier punto en la curva. La curva es representada matemáticamente por un polinomio de grado uno menos el orden de la curva. Por lo tanto, las curvas de segundo orden (que están representadas por polinomios lineales) se denominan curvas lineales, las curvas de tercer orden, se denominan curvas cuadráticas, y las curvas de cuarto orden se denominan curvas cúbicas. El número de puntos de control debe ser mayor que o igual al orden de la curva.
En la práctica, las curvas cúbicas son las más utilizadas. Las curvas de quinto y sexto orden a veces son útiles, sobre todo para la obtención de derivadas continuas de orden mayor, pero las curvas de órdenes más altos prácticamente nunca se utiliza porque conducen a problemas numéricos internos y tienden a requerir tiempos de cálculo desproporcionadamente grandes.
Referencias
- Les Piegl & Wayne Tiller: The NURBS Book, Springer-Verlag 1995–1997 (2nd ed.). The main reference for Bézier, B-Spline and NURBS; chapters on mathematical representation and construction of curves and surfaces, interpolation, shape modification, programming concepts.
- Dr. Thomas Sederberg, BYU NURBS, https://web.archive.org/web/20060227192446/http://cagd.cs.byu.edu/~557/text/ch5.pdf
- Dr. Lyle Ramshaw. Blossoming: A connect-the-dots approach to splines, Research Report 19, Compaq Systems Research Center, Palo Alto, CA, June 1987
- David F. Roger: An Introduction to NURBS with Historical Perspective, Morgan Kaufmann Publishers 2001. Good elementary book for NURBS and related issues.
- Foley, van Dam, Feiner & Hughes: Computer Graphics - Principles and Practice, Addison Wesley 1996 (2nd ed.).
Notas
- David F. Rogers: An Introduction to NURBS with Historical Perspective, section 7.1
- Demidov, Evgeny. «NonUniform Rational B-splines (NURBS) - Perspective projection». An Interactive Introduction to Splines. Ibiblio. Consultado el 14 de febrero de 2010.
Enlaces externos
- Acerca de los NURBS (en inglés)
- Una introducción interactiva a los NURBS (en inglés)
- Bézier Surfaces (en inglés)