Nudo trivial
En la teoría de nudos matemática, un nudo trivial es aquel que presenta una configuración sin nudos (también denominada carente de nudos o desanudada), que corresponde al menos anudado de todos los nudos. Intuitivamente, un nudo trivial es un lazo cerrado de cuerda sin un nudo, es decir, sin anudamiento alguno. Para un teórico de nudos, un desanudado es cualquier circunferencia topológica embebida en una 3-esfera que es ambientalmente isotópica (es decir, deformable), de manera que se puede asociar con una circunferencia geométrica, el desanudado estándar.
| Nudo trivial | ||
|---|---|---|
 | ||
| Nombre común | Circunferencia | |
| Invariante de Arf | 0 | |
| nº de trenzas | 1 | |
| nº de puentes | 0 | |
| nº de cruces | 0 | |
| Genus | 0 | |
| nº de enlaces | 0 | |
| nº de barras | 3 | |
| nº de túneles | 0 | |
| nº de desanudados | 0 | |
| Notación de Conway | - | |
| Notación A–B | 01 | |
| Notación de Dowker | - | |
| Siguiente | 31 | |
| Otras propiedades | ||
| • Toroidal • Fibrado • Primo • Rebanada • Totalmente anfiquiral | ||

El desanudado es el único nudo que es el límite de un disco incrustado, lo que da la caracterización de que solo los desanudados tienen genus de Seifert 0. De manera similar, el desanudado es el elemento neutro con respecto a la operación suma conexa.
Problema de desanudado
Decidir si un nudo en particular es trivial fue una fuerza impulsora importante detrás del desarrollo de los invariantes de nudos, ya que se pensó que este enfoque posiblemente proporcionaría un algoritmo eficiente para reconocer nudos triviales a partir de alguna presentación como parte de la teoría de nudos. Se sabe que el reconocimiento de nudos triviales puede presentar dificultad tanto NP como co-NP.
También se sabe que la homología de nudos de Floer y la homología de Khovanov detectan el desanudado, pero se desconoce que sean computables eficientemente para este propósito. No se sabe si el polinomio de Jones o los invariantes de tipo finito son capaces de detectar el desanudado.
Ejemplos
Puede ser difícil encontrar una manera de desenredar una cuerda, aunque el hecho de que comenzó desenredada demuestra que la tarea es posible. Thistlethwaite y Ochiai proporcionaron muchos ejemplos de diagramas de nudos que no tienen una forma obvia de simplificarlos a medida que se aumenta el número de cruces del diagrama.
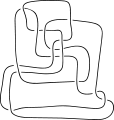 Nudo trivial de Thistlethwaite
Nudo trivial de Thistlethwaite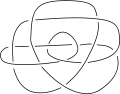 Uno de los nudos triviales de Ochiai
Uno de los nudos triviales de Ochiai
Si bien la cuerda generalmente no tiene la forma de un bucle cerrado, también se considera una forma canónica en la que se imagina que los extremos están unidos. Desde este punto de vista, muchos nudos prácticos útiles son en realidad nudos triviales, incluidos los que se pueden atar en una cuerda combada.[1]
Cada nudo se puede representar como un enlace mecánico, que es una colección de segmentos de línea rígidos conectados por juntas universales en sus puntos finales. El número de barras es el número mínimo de segmentos necesarios para representar un nudo como un enlace, y un desanudado atascado es un enlace particular sin anudar que no se puede reconfigurar en un polígono convexo plano.[2] Al igual que el número de cruces, es posible que sea necesario dar forma a un enlace más complejo subdividiendo sus segmentos antes de que pueda simplificarse.
Invariantes
Los polinomios de Alexander-Conway y los polinomios de Jones de una configuración sin nudos son triviales:
Ningún otro nudo con 10 cruces o menos tiene un polinomio de Alexander trivial, pero el nudo de Kinoshita-Terasaka y el nudo de Conway (ambos tienen 11 cruces) tienen los mismos polinomios de Alexander y Conway que el nudo. Es un problema abierto si cualquier nudo no trivial tiene el mismo polinomio de Jones que el nudo trivial.
El desanudado es el único nudo cuyo grupo de nudo es un grupo cíclico infinito, y su complemento de nudo es homeomofo a un toro sólido.
Véase también
Referencias
- Volker Schatz. «Knotty topics». Archivado desde el original el 17 de julio de 2011. Consultado el 23 de abril de 2007.
- Godfried Toussaint (2001). «A new class of stuck unknots in Pol-6». Contributions to Algebra and Geometry 42 (2): 301-306. Archivado desde el original el 12 de mayo de 2003.
Enlaces externos
- Knot Atlas
- Weisstein, Eric W. «Nudo trivial». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.