Optimización bayesiana
La optimización bayesiana es una estrategia de diseño secuencial para la optimización global de funciones de caja negra[1][2][3] que no asume ninguna forma funcional. Suele emplearse para optimizar funciones caras de evaluar.
Historia
El término se atribuye generalmente a Jonas Mockus [lt] y se acuña en su obra a partir de una serie de publicaciones sobre optimización global en las décadas de 1970 y 1980.[4][5][1]
Estrategia
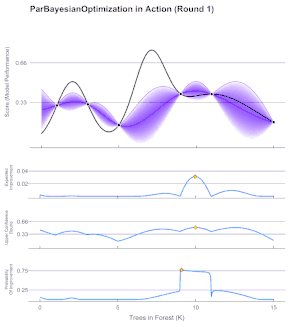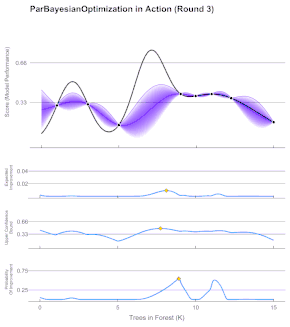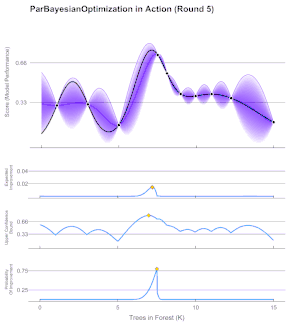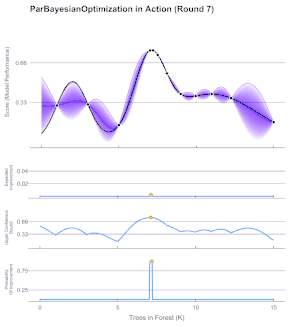
La optimización bayesiana se utiliza normalmente en problemas de la forma , donde es un conjunto de puntos, que se basan en menos de 20 dimensiones (), y cuya pertenencia puede evaluarse fácilmente. La optimización bayesiana es especialmente ventajosa para problemas en los que es difícil de evaluar debido a su coste computacional. La función objetivo, , es continua y adopta la forma de una estructura desconocida, denominada "caja negra". Tras su evaluación, sólo se observa y sus derivadas no se evalúan.[7]
Dado que la función objetivo es desconocida, la estrategia bayesiana consiste en tratarla como una función aleatoria y colocar una prioridad sobre ella. El prior recoge las creencias sobre el comportamiento de la función. Después de recoger las evaluaciones de la función, que se tratan como datos, se actualiza la priorización para formar la distribución posterior sobre la función objetivo. La distribución posterior, a su vez, se utiliza para construir una función de adquisición (a menudo también denominada criterio de muestreo de relleno) que determina el siguiente punto de consulta.
Existen varios métodos para definir la distribución a priori/posterior sobre la función objetivo. Los dos métodos más comunes utilizan procesos gaussianos en un método denominado kriging. Otro método menos costoso utiliza el estimador de Parzen para construir dos distribuciones para los puntos "altos" y "bajos" y, a continuación, encuentra la ubicación que maximiza la mejora esperada.[8]
La optimización bayesiana estándar se basa en que cada es fácil de evaluar y los problemas que se desvían de este supuesto se conocen como problemas exóticos de optimización bayesiana. Los problemas de optimización pueden llegar a ser exóticos si se sabe que hay ruido, las evaluaciones se realizan en paralelo, la calidad de las evaluaciones depende de un compromiso entre dificultad y precisión, la presencia de condiciones ambientales aleatorias o si la evaluación implica derivadas.[7]
Funciones de adquisición
Ejemplos de funciones de adquisición:
- probabilidad de mejora
- mejora prevista
- Pérdidas esperadas bayesianas
- límites superiores de confianza (LCR) o límites inferiores de confianza
- Muestreo Thompson
Junto con híbridos de éstos.[9] Todos ellos compensan la exploración y la explotación para minimizar el número de consultas de funciones. Como tal, la optimización bayesiana es muy adecuada para funciones que son caras de evaluar.
Métodos de solución
El máximo de la función de adquisición suele encontrarse recurriendo a la discretización o mediante un optimizador auxiliar. Las funciones de adquisición suelen comportarse bien y se maximizan mediante una técnica de optimización numérica, como el método de Newton o métodos cuasi-Newton como el algoritmo Broyden-Fletcher-Goldfarb-Shanno.
Aplicaciones
El enfoque se ha aplicado para resolver una amplia gama de problemas,[10] entre los que se incluyen aprender a clasificar,[11] gráficos por computadora y diseño visual,[12][13][14] robótica,[15][16][17][18] redes de sensores,[19][20] configuración automática de algoritmos,[21][22] cajas de herramientas de aprendizaje automático de máquinas,[23][24][25] aprendizaje por refuerzo,[26] planificación, atención visual, configuración de arquitecturas en aprendizaje profundo, análisis estático de programas, física experimental de partículas,[27][28] optimización de la calidad-diversidad,[29][30][31] química, diseño de materiales y desarrollo de fármacos.[7][32][33]
Véase también
- Bandido multibrazo
- Kriging
- Muestreo de Thompson
- Optimización global
- Diseño experimental bayesiano
- Probabilística numérica
- Óptimo de Pareto
- Dilución de regresión
- Estimación bayesiana recursiva
Referencias
- Močkus, J. (1989). «Bayesian Approach to Global Optimization. Dordrecht». Kluwer Academic. ISBN 0-7923-0115-3.
- Garnett, Roman. «Bayesian Optimization Book». Bayesian Optimization Book (en inglés estadounidense). Consultado el 19 de septiembre de 2023.
- Hennig, P.; Osborne, M. A.; Kersting, H. P. (2022). «Probabilistic Numerics». Cambridge University Press: 243-278. ISBN 978-1107163447.
- Močkus, Jonas (1975). «On bayesian methods for seeking the extremum». Optimization Techniques IFIP Technical Conference Novosibirsk, July 1–7, 1974. Lecture Notes in Computer Science. Vol. 27: 400-404. ISBN 978-3-540-07165-5. doi:10.1007/3-540-07165-2_55.
- Močkus, Jonas (1977). «On Bayesian Methods for Seeking the Extremum and their Application». IFIP Congress: 195-200.
- Wilson, Samuel Von (4 de julio de 2023), Parallelizable Bayesian Optimization, consultado el 19 de septiembre de 2023.
- Frazier, Peter I. (2018). A Tutorial on Bayesian Optimization.
- J. S. Bergstra, R. Bardenet, Y. Bengio, B. Kégl (2011). «Algorithms for Hyper-Parameter Optimization». Advances in Neural Information Processing Systems: 2546-2554.
- Matthew W. Hoffman, Eric Brochu, Nando de Freitas (2011). «Portfolio Allocation for Bayesian Optimization». Uncertainty in Artificial Intelligence: 327-336.
- Eric Brochu, Vlad M. Cora, Nando de Freitas (2010). «A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning». CoRR.
- Eric Brochu, Nando de Freitas, Abhijeet Ghosh (2007). «Active Preference Learning with Discrete Choice Data». Advances in Neural Information Processing Systems: 409-416.
- Eric Brochu, Tyson Brochu, Nando de Freitas (2010). «A Bayesian Interactive Optimization Approach to Procedural Animation Design». Symposium on Computer Animation.
- Yuki Koyama, Issei Sato, Daisuke Sakamoto, Takeo Igarashi (2017). «Sequential Line Search for Efficient Visual Design Optimization by Crowds». Transactions on Graphics, Volume 36, Issue 4: 48:1-48:11. doi:10.1145/3072959.3073598.
- Koyama, Yuki; Sato, Issei; Goto, Masataka (31 de agosto de 2020). «Sequential Gallery for Interactive Visual Design Optimization». ACM Transactions on Graphics 39 (4). ISSN 0730-0301. doi:10.1145/3386569.3392444. Consultado el 20 de septiembre de 2023.
- Daniel J. Lizotte, Tao Wang, Michael H. Bowling, Dale Schuurmans (2017). «Automatic Gait Optimization with Gaussian Process Regression». International Joint Conference on Artificial Intelligence: 944-949.
- Martinez-Cantin, Ruben; de Freitas, Nando; Brochu, Eric; Castellanos, José; Doucet, Arnaud (1 de agosto de 2009). «A Bayesian exploration-exploitation approach for optimal online sensing and planning with a visually guided mobile robot». Autonomous Robots (en inglés) 27 (2): 93-103. ISSN 1573-7527. doi:10.1007/s10514-009-9130-2. Consultado el 20 de septiembre de 2023.
- Scott Kuindersma, Roderic Grupen, and Andrew Barto (2013). «Variable Risk Control via Stochastic Optimization». International Journal of Robotics Research, volume 32, number 7: 806-825.
- Calandra, Roberto; Seyfarth, André; Peters, Jan; Deisenroth, Marc Peter (1 de febrero de 2016). «Bayesian optimization for learning gaits under uncertainty». Annals of Mathematics and Artificial Intelligence (en inglés) 76 (1): 5-23. ISSN 1573-7470. doi:10.1007/s10472-015-9463-9. Consultado el 20 de septiembre de 2023.
- Niranjan Srinivas, Andreas Krause, Sham M. Kakade, Matthias W. Seeger (2012). «Information-Theoretic Regret Bounds for Gaussian Process Optimization in the Bandit Setting». IEEE Transactions on Information Theory: 3250-3265.
- Roman Garnett, Michael A. Osborne, Stephen J. Roberts: (2010). «Bayesian optimization for sensor set selection». ACM/IEEE International Conference on Information Processing in Sensor Networks: 209-219.
- Frank Hutter, Holger Hoos, and Kevin Leyton-Brown (2011). «http://www.cs.ubc.ca/labs/beta/Projects/SMAC/papers/11-LION5-SMAC.pdf». Learning and Intelligent Optimization.
- J. Snoek, H. Larochelle, R. P. Adams (2012). «Practical Bayesian Optimization of Machine Learning Algorithms». Advances in Neural Information Processing Systems.
- J. Bergstra, D. Yamins, D. D. Cox (2013). «Hyperopt: A Python Library for Optimizing the Hyperparameters of Machine Learning Algorithms». Proc. SciPy 2013.
- Chris Thornton, Frank Hutter, Holger H. Hoos, Kevin Leyton-Brown (2013). «Auto-WEKA: combined selection and hyperparameter optimization of classification algorithms». KDD: 847-855.
- Jasper Snoek, Hugo Larochelle and Ryan Prescott Adams (2012). «Practical Bayesian Optimization of Machine Learning Algorithms». Advances in Neural Information Processing Systems.
- Berkenkamp, Felix (2019). Safe Exploration in Reinforcement Learning: Theory and Applications in Robotics (en inglés). ETH Zurich. Consultado el 20 de septiembre de 2023.
- Ilten, Philip; Williams, Mike; Yang, Yunjie (27 de abril de 2017). «Event generator tuning using Bayesian optimization». Journal of Instrumentation 12 (04): P04028-P04028. ISSN 1748-0221. doi:10.1088/1748-0221/12/04/P04028. Consultado el 20 de septiembre de 2023.
- Cisbani, E.; Dotto, A. Del; Fanelli, C.; Williams, M.; Alfred, M.; Barbosa, F.; Barion, L.; Berdnikov, V. et al. (19 de mayo de 2020). «AI-optimized detector design for the future Electron-Ion Collider: the dual-radiator RICH case». Journal of Instrumentation 15 (05): P05009-P05009. ISSN 1748-0221. doi:10.1088/1748-0221/15/05/p05009. Consultado el 20 de septiembre de 2023.
- Kent, Paul; Gaier, Adam; Mouret, Jean-Baptiste; Branke, Juergen (2023). BOP-Elites, a Bayesian Optimisation Approach to Quality Diversity Search with Black-Box descriptor functions.
- Kent, Paul; Branke, Juergen (12 de julio de 2023). «Bayesian Quality Diversity Search with Interactive Illumination». Proceedings of the Genetic and Evolutionary Computation Conference. GECCO '23 (Association for Computing Machinery): 1019-1026. ISBN 979-8-4007-0119-1. doi:10.1145/3583131.3590486. Consultado el 20 de septiembre de 2023.
- Gaier, Adam; Asteroth, Alexander; Mouret, Jean-Baptiste (2018). «Data-Efficient Design Exploration through Surrogate-Assisted Illumination». Evolutionary Computation. doi:10.1162/evco_a_00231.
- Gómez-Bombarelli, Rafael; Wei, Jennifer N.; Duvenaud, David; Hernández-Lobato, José Miguel; Sánchez-Lengeling, Benjamín; Sheberla, Dennis; Aguilera-Iparraguirre, Jorge; Hirzel, Timothy D. et al. (28 de febrero de 2018). «Automatic Chemical Design Using a Data-Driven Continuous Representation of Molecules». ACS Central Science (en inglés) 4 (2): 268-276. ISSN 2374-7943. PMC 5833007. PMID 29532027. doi:10.1021/acscentsci.7b00572. Consultado el 20 de septiembre de 2023.
- Griffiths, Ryan-Rhys; Miguel Hernández-Lobato, José (2020). «Constrained Bayesian optimization for automatic chemical design using variational autoencoders». Chemical Science (en inglés) 11 (2): 577-586. doi:10.1039/C9SC04026A. Consultado el 20 de septiembre de 2023.