Politopo simple

En geometría, un politopo simple de d dimensiones es un politopo también de d dimensiones, cada uno de cuyos vértices son adyacentes exactamente a d aristas (y en consecuencia, también a d caras). La figura de vértice de un d-politopo simple es un (d -1)-símplex.[1]

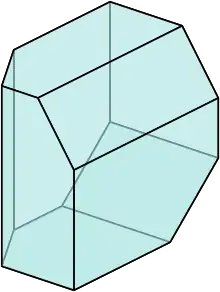
Asociaedro tridimensional. Cada vértice tiene tres aristas y tres caras incidentes, por lo que es un poliedro simple

Los politopos simples son topológicamente duales a politopos simpliciales. La familia de politopos que son a la vez simples y simpliciales son símplices o polígonos bidimensionales. Un poliedro simple es un poliedro tridimensional cuyos vértices son adyacentes a tres aristas y tres caras. El poliedro dual de uno simple es otro poliedro simple, en el que todas sus caras son triángulos.[2]

Ejemplos

Entre los poliedros simples tridimensionales figuran los prismas (incluido el cubo), el tetraedro regular y el dodecaedro y, entre los sólidos arquimedianos, el tetraedro truncado, el cubo truncado, el octaedro truncado, el cuboctaedro truncado, el dodecaedro truncado, el icosaedro truncado y el icosidodecaedro truncado. También figuran los poliedros de Goldberg y los fullerenos, incluidos el tetraedro biselado, el cubo biselado y el dodecaedro biselado. En general, cualquier poliedro puede convertirse en uno simple mediante el truncamiento de sus vértices de valencia cuatro o superior. Por ejemplo, los trapezoedros truncados se forman truncando únicamente los vértices de mayor grado de un trapezoedro; y por lo tanto también son simples.

Los politopos simples de cuatro dimensiones incluyen el 120-celdas y el teseracto regulares. Los 4-politopos uniformes simples incluyen al 5-celdas truncado, al teseracto truncado, al 24-celdas truncado, al 120-celdas truncado y al duoprisma. Todos los 4-politopos bitruncados, cantitruncados u omnitruncados son simples.

Los politopos simples en dimensiones superiores incluyen los politopos d-símplex, hipercubo, asociaedro, permutoedro y todos los omnitruncados.

Reconstrucción única

Micha Perles conjeturó que un politopo simple está completamente determinado por su 1-esqueleto. Su conjetura fue probada en 1987 por Roswitha Blind y Peter Mani-Levitska.[3] Gil Kalai poco después proporcionó una prueba más simple de este resultado, basada en la teoría de la orientación única del sumidero.[4]

Referencias
  1. Ziegler, Günter M. (2012), Lectures on Polytopes, Graduate Texts in Mathematics 152, Springer, p. 8, ISBN 9780387943657.
  2. Cromwell, Peter R. (1997), Polyhedra, Cambridge University Press, p. 341, ISBN 0-521-66405-5.
  3. Blind, Roswitha; Mani-Levitska, Peter (1987), «Puzzles and polytope isomorphisms», Aequationes Mathematicae 34 (2-3): 287-297, MR 921106, doi:10.1007/BF01830678.
  4. Kalai, Gil (1988), «A simple way to tell a simple polytope from its graph», Journal of Combinatorial Theory, Series A 49 (2): 381-383, MR 964396, doi:10.1016/0097-3165(88)90064-7.
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.