Precesión apsidal
En mecánica celeste, la precesión apsidal (o avance apsidal)[1] es la precesión (rotación gradual) de la línea que conecta los ápsides (línea de los ápsides) de la órbita de un cuerpo astronómico. Los ápsides son los puntos orbitales más cercanos (periapsis) y más alejados (apoapsis) de su cuerpo primario. La precesión apsidal es la primera derivada temporal del argumento del periapsis, uno de los seis elementos orbitales principales de una órbita. La precesión apsidal se considera positiva cuando el eje de la órbita gira en la misma dirección que el movimiento orbital. El período apsidal es el intervalo de tiempo necesario para que una órbita precese 360°.[2]
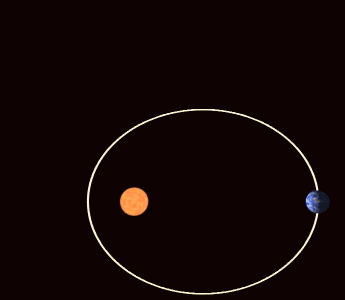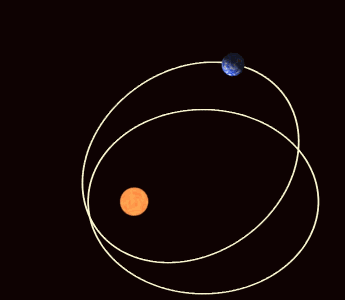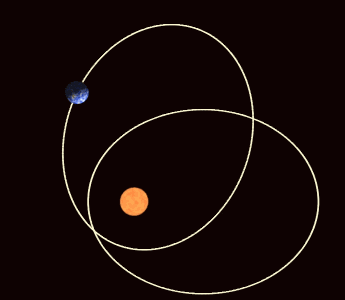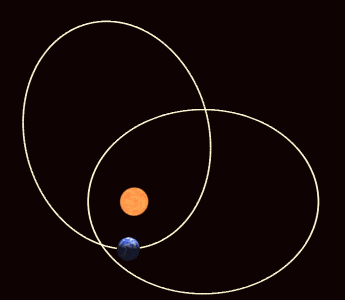
Historia
El antiguo astrónomo griego Hipparchos notó la precesión apsidal de la órbita de la Luna;[3] se corrige en el Mecanismo de Antikythera (alrededor del 80 a. C.) con el valor casi exactamente exacto de 8.88 años por ciclo completo, correcto dentro del 0.34%.[4] La precesión de los ápsides solares fue descubierta en el siglo XI por al-Zarqālī.[5] La precesión apsidal lunar no se tuvo en cuenta en el Almagesto de Ptolomeo, y como grupo, estas precesiones, resultado de una plétora de fenómenos, siguieron siendo difíciles de explicar hasta el siglo XX, cuando se explicó con precisión la última parte no identificada de la precesión de Mercurio.
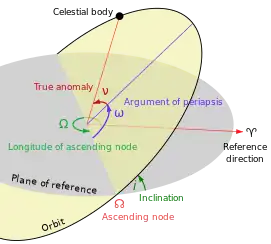
Cálculo
Varios factores pueden llevar a la precesión periastrónica tales como la relatividad general, el cuadripolo de momentos estelares, las deformaciones mareales mutuas entre estrella-planeta y las perturbaciones provenientes de otros planetas:[6]
- ωtotal = ωrelatividad general + ωcuadrupolo + ωmarea + ωperturbaciones
La tasa de precesión perihélica para Mercurio debido a efectos relativistas es de 43'' (segundos de arco) por siglo. Por comparación, la precesión debido a perturbaciones debida a otros planetas del Sistema Solar puede rondar los 532'' por siglo, mientras que la contribución por el achatamiento del Sol (momento cuadripolo) causa una contribución mínima de 0,025'' por siglo.[7][8]
Para mecánica clásica, si las estrellas y planetas son considerados masas esféricas puras, entonces obedecerían a la ley de la inversa del cuadrado 1r2, relativa a la fuerza por la distancia y por tanto ejecutar órbitas elípticas cercanas de acuerdo con el teorema de Bertrand. Los efectos de las masas no esféricas son causados por la aplicación de potenciales externos: la fuerza centrífuga de un cuerpo en rotación causa su achatamiento (como una masa de pizza al girar) mientras que la marea provoca abultamientos hacia la masa más cercana.
Estos abultamientos rotacionales o mareales crean campos gravitacionales cuadripolos 1r3 que afectan a la precesión orbital.
La precesión total apsidal para planetas muy grandes, con masas móviles, como planetas jupiterianos calientes es, considerando las menores perturbaciones, en orden de importancia:
- ωtotal = ωperturbaciones mareales + ωrelatividad general + ωperturbaciones rotacionales + ωrotacional * + ωmareal*
con el abultamiento mareal planetario siendo el término dominante, excediendo los efectos de la relatividad general y el cuadripolo estelar por más de un orden de magnitud. La buena aproximación resultante por el abultamiento mareal es útil para entender el interior de esos planetas. Para planetas con períodos más cortos, el interior del planeta induce una precesión de algunos grados por años. Por ejemplo, para el planeta extrasolar WASP-12b es de 19,9º por año.[9][10]
Teorema de Newton de las órbitas de revolución
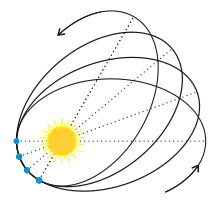
Newton derivó un teorema temprano que intentaba explicar la precesión apsidal. Este teorema es históricamente notable, pero nunca se usó ampliamente y proponía fuerzas que se ha descubierto que no existen, lo que invalida el teorema. Este teorema de las órbitas giratorias permaneció en gran parte desconocido y sin desarrollar durante más de tres siglos hasta 1995. Newton propuso que las variaciones en el movimiento angular de una partícula se pueden explicar mediante la adición de una fuerza que varía como el cubo inverso de la distancia, sin afectar el movimiento radial de una partícula.[cita requerida] Usando un precursor de la serie Taylor Newton generalizó su teorema a todas las leyes de la fuerza siempre que las desviaciones de las órbitas circulares sean pequeñas, lo que es válido para la mayoría de los planetas del Sistema Solar.[cita requerida] Sin embargo, su teorema no explica la precesión apsidal de la Luna sin renunciar a la ley del inverso del cuadrado de la ley de Newton de la gravitación universal. Además, la tasa de precesión apsidal calculada mediante el teorema de Newton de las órbitas giratorias no es tan precisa como lo es para los métodos más nuevos, como la teoría de la perturbación.
Relatividad general
Artículo principal: Problema de Kepler en relatividad general
Urbain Le Verrier notó una precesión apsidal del planeta Mercurio a mediados del siglo XIX y la explica la teoría general de la relatividad de Einstein.
Einstein demostró que para un planeta, el semieje principal de su órbita es a, la excentricidad de la órbita e y el período de revolución T, entonces la precesión apsidal debida a efectos relativistas, durante un período de revolución en radianes, es
donde c es la velocidad de la luz.[11] En el caso de Mercurio, la mitad del eje mayor es aproximadamente 5.79 × 1010 m, la excentricidad de su órbita es 0.206 y el período de revolución 87.97 días o 7,6 × 106 s. De estos y la velocidad de la luz (que es ~3 × 108 m/s), se puede calcular que la precesión apsidal durante un período de revolución es ε = 5,028 × 10−7 radianes (2,88 × 10−5 grados o 0,104″). En cien años, Mercurio da aproximadamente 415 revoluciones alrededor del Sol, y así, en ese tiempo, el perihelio apsidal debido a efectos relativistas es aproximadamente 43″, que corresponde casi exactamente a la parte previamente inexplicada del valor medido.
Clima a largo plazo
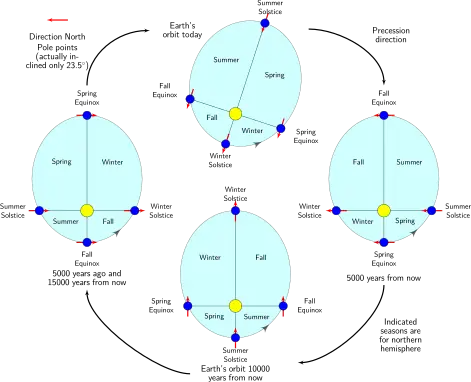
La precesión apsidal de la Tierra aumenta lentamente su argumento de periapsis; Se tarda como 112.000 años para que la elipse gire una vez en relación con las estrellas fijas.[12] El eje polar de la Tierra, y por lo tanto los solsticios y equinoccios, precesan con un período de aproximadamente 26 000 años en relación con las estrellas fijas. Estas dos formas de 'precesión' se combinan de modo que toma entre 20,800 y 29.000 años (y en promedio 23.000 años) para que la elipse gire una vez en relación con el equinoccio de primavera, es decir, para que el perihelio vuelva a la misma fecha (dado un calendario que rastrea perfectamente las estaciones).[13]
Esta interacción entre el ciclo anomalístico y tropical es importante en las variaciones climáticas a largo plazo en la Tierra, llamadas ciclos de Milankovitch. También se conoce un equivalente en Marte.
La figura de la derecha ilustra los efectos de la precesión en las estaciones del hemisferio norte, en relación con el perihelio y el afelio. Observe que las áreas barridas durante una temporada específica cambian con el tiempo. La mecánica orbital requiere que la duración de las estaciones sea proporcional a las áreas barridas de los cuadrantes estacionales, por lo que cuando la excentricidad orbital es extrema, las estaciones en el lado lejano de la órbita pueden ser sustancialmente más largas.
Véase también
- Precesión axial
- Precesión nodal
- Precesión apsidal lunar
- Hipotrocoide
- Rosseta (órbita)
- Espirógrafo
Referencias
- «Avance apsidal».
- «Introducción a las estrellas binarias cercanas».
- «La adaptación de los métodos babilónicos en la astronomía numérica griega». Archivado desde el original el 4 de marzo de 2016. Consultado el 13 de enero de 2021.
- «Decodificación de la calculadora astronómica griega antigua conocida como el mecanismo de Antikythera». Archivado desde el original el 20 de julio de 2015. Consultado el 13 de enero de 2021.
- «La teoría solar de al-Zarqali».
- David M. Kipping (8 de agosto de 2011). The Transits of Extrasolar Planets with Moons. Springer. pp. 84-. ISBN 978-3-642-22269-6. Consultado el 27 de agosto de 2013.
- Kane, S. R.; Horner, J.; von Braun, K. (2012). «Cyclic Transit Probabilities of Long-period Eccentric Planets due to Periastron Precession». The Astrophysical Journal 757 (1): 105. Bibcode:2012ApJ...757..105K. arXiv:1208.4115. doi:10.1088/0004-637x/757/1/105.
- Richard Fitzpatrick (30 de junio de 2012). An Introduction to Celestial Mechanics. Cambridge University Press. p. 69. ISBN 978-1-107-02381-9. Consultado el 26 de agosto de 2013.
- Ragozzine, D.; Wolf, A. S. (2009). «Probing the interiors of very hot Jupiters using transit light curves». The Astrophysical Journal 698 (2): 1778. Bibcode:2009ApJ...698.1778R. arXiv:0807.2856. doi:10.1088/0004-637x/698/2/1778.
- Michael Perryman (26 de mayo de 2011). The Exoplanet Handbook. Cambridge University Press. pp. 133-. ISBN 978-1-139-49851-7. Consultado el 26 de agosto de 2013.
- «Sobre los hombros de gigantes: las grandes obras de la física y la astronomía».
- «Revista geofísica internacional».
- «Observatorio Naval de EE.UU.». Archivado desde el original el 2 de agosto de 2013. Consultado el 13 de enero de 2021.