Primeros analíticos

Primeros analíticos (en griego antiguo Ἀναλυτικῶν προτέρων, en latín Analytica priora, abreviado An. Pr[1]) es un texto del filósofo griego Aristóteles. Se compone de dos libros (I: 71a - 89b, II: 90a - 100b) y no existen dudas acerca de la autenticidad de la obra. Es el tercer libro del Órganon, en el que sucede a De la interpretación y precede a Segundos analíticos. En algunas ediciones, se traduce Ἀναλυτικῶν προτέρων por Analíticos anteriores.

Primeros analíticos
de Aristóteles

Prior Analytics en la Biblioteca Laurenciana, c. 1290
Tema(s) Lógica
Edición original en griego antiguo
Título original Ἀναλυτικὰ Πρότερα
Edición traducida al español
Título Primeros analíticos

Primeros analíticos es uno de los textos más importantes no sólo de Aristóteles sino también de la propia lógica, ya que en ese texto presenta el filósofo su teoría del silogismo. El texto se ocupa del análisis de los argumentos según sus formas, es decir, según las varias figuras y modos del silogismo.

En palabras de Aristóteles:

"Nuestra primera tarea consiste en indicar el objeto de estudio de nuestra investigación y a qué ciencia pertenece éste; qué concierne a la demostración y qué pertenece a una ciencia demostrativa. Enseguida tendremos que definir el significado de premisa, término y silogismo, y distinguir entre un silogismo perfecto y uno imperfecto; después de eso, necesitaremos explicar en qué sentido se dice que un término está o no está enteramente contenido en otro y qué entendemos por ser predicado de todo o de ninguno." (An. Pr., 24a).

Contenido
Commentaria in Analytica priora Aristotelis, 1549

Libro I

El libro I trata específicamente de la teoría del silogismo.

El silogismo
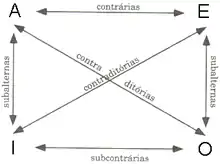
Esta sección es un extracto de Lógica aristotélica § Silogismos.[editar]
Se llama cuadro de oposición al esquema mediante el cual se estudian las relaciones formales entre los diversos tipos de juicios aristotélicos, considerando cada juicio con términos idénticos:
- A = Universal afirmativo. Término Sujeto tomado en su extensión universal; término Predicado particular; cualidad afirmativa (Todo S es P).
- E = Universal negativo. Término Sujeto tomado en su extensión universal; término Predicado universal; cualidad negativa (Ningún S es P).
- I = Particular afirmativo. Término Sujeto tomado en su extensión particular; término Predicado en su extensión particular; cualidad afirmativa (Algún S es P).
- O = Particular negativo. Término Sujeto tomado en su extensión particular; término Predicado en su extensión universal; cualidad negativa (Algún S no es P).

Según Aristóteles, toda proposición (apophansis) se compone de dos términos (horos), un sujeto (hipokeimenon) y un predicado (katêgorein); y puede ser verdadera o falsa.[2] Luego, todo enunciado afirmativo simple se puede reducirse a "S es P".[3]

La noción central del sistema lógico de Aristóteles es el silogismo (o deducción, apódeixis o sullogismos).[4][5] Un silogismo es, según la definición de Aristóteles, «un discurso (logos) en el cual, establecidas ciertas cosas, resulta necesariamente de ellas, por ser lo que son, otra cosa diferente».[6] El silogismo es una inferencia en la que una conclusión (sumperasma) se sigue necesariamente de otras dos proposiciones, las "premisas" (protasis).[3] Un ejemplo clásico de silogismo es el siguiente:

  1. Todos los hombres son mortales.
  2. Todos los griegos son hombres.
  3. Por lo tanto, todos los griegos son mortales.

En este ejemplo, tras establecer las premisas (1) y (2), la conclusión (3) se sigue por necesidad. La noción de silogismo es similar a la noción moderna de argumento deductivamente válido, pero hay diferencias.[7]

En los Primeros analíticos, Aristóteles construyó la primera teoría de la inferencia válida.[8] Conocida como la silogística, la teoría ofrece criterios para evaluar la validez de ciertos tipos muy específicos de silogismos: los silogismos categóricos.[8] Para definir lo que es un silogismo categórico, primero es necesario definir lo que es una proposición categórica. Toda proposición contiene dos términos: un sujeto (S) y un predicado (P). Una proposición es categórica si tiene alguna de las siguientes cuatro formas:

  • Universal afirmativo (A) = Todo S es P —por ejemplo, todos los humanos son mamíferos.
  • Universal negativo (E) = Ningún S es P —por ejemplo, ningún humano es un reptil.
  • Particular afirmativo (I) = Algunos S son P —por ejemplo, algunos humanos son varones.
  • Particular negativo (O) = Algunos S no son P —por ejemplo, algunos humanos no son varones.

A partir de estos cuatro ejes, Aristóteles en su obra Sobre la interpretación muestra un cuadro de oposición de los juicios (ver imagen de la derecha), donde se relaciona los valores de verdad entre cada jucio categórico. De ellos surgen jucios contrarios (A-E ), subcontrarios (I-O), contradictorios (A-O e I-E) y subalternos (A-I e E-O).[9]

Un silogismo es categórico si está compuesto por exactamente tres proposiciones categóricas (dos premisas y una conclusión), y si ambas premisas comparten exactamente un término (llamado el término medio), que además no está presente en la conclusión. Por ejemplo, el silogismo mencionado más arriba es un silogismo categórico. Dadas estas definiciones, existen tres maneras en que el término medio puede estar distribuido entre las premisas. Sean A, B y C tres términos distintos, luego:

Primera figura Segunda figura Tercera figura
Sujeto Predicado Sujeto Predicado Sujeto Predicado
Premisa A B A B A C
Premisa B C A C B C
Conclusión A C B C A B
Aristóteles llama a estas tres posibilidades figuras.[10] El silogismo mencionado más arriba es una instancia de la primera figura. Dado que cada silogismo categórico consta de tres proposiciones categóricas, y que existen cuatro tipos de proposiciones categóricas, y tres tipos de figuras, existen 4 × 4 × 4 × 3 = 192 silogismos categóricos distintos. Algunos de estos silogismos son válidos, otros no. Para distinguir unos de otros, Aristóteles parte de dos silogismos categóricos que asume como válidos (algo análogo a las actuales reglas de inferencia), y demuestra a partir de ellos (con ayuda de tres reglas de conversión), la validez de todos y solo los silogismos categóricos válidos.[8]

Libro II

El libro II trata de las propiedades del silogismo, falsas conclusiones y razonamientos próximos al silogismo.

Influencia

Los Primeros analíticos de Aristóteles representa la primera vez en la historia cuando la lógica se investiga científicamente. Solo por esas razones, Aristóteles podría ser considerado el padre de la lógica, ya que él mismo lo dice en Refutaciones sofísticas: "... En lo que respecta a este tema, no es el caso que esa parte haya sido elaborada antes de antemano y otra parte haya no; en cambio, nada existía en absoluto ".[11]

En el siglo III d. C., el comentario de Alejandro de Afrodisias sobre Analytica prioras es el más antiguo y uno de los mejores de la tradición antigua.[12]

En el siglo VI, Boecio compuso la primera traducción latina conocida de Analytica priora No se sabe que ningún occidental entre Boecio y Bernardo de Utrecht haya leído el Primeros analítico. [8] El llamado Anonymus Aurelianensis III de la segunda mitad del siglo XII es el primer comentario latino existente, o más bien el fragmento de un comentario.[13]

En los tiempos modernos, esta definición ha llevado a un debate sobre cómo debe interpretarse la palabra "silogismo". Los académicos Jan Lukasiewicz, Józef Maria Bocheński y Günther Patzig se han aliado con la dicotomía Protasis - Apódosis, mientras que John Corcoran prefiere considerar un silogismo como una simple deducción.[14][15]

Referencias
  1. Ross, W. D. (William David), 1877-1971. Aristotle (Diego F. Pró, trad.) [Aristóteles]. CHARCAS BUENOS AIRES. Consultado el 9 de septiembre de 2019.
  2. Véase la sección «Lógica» en Shields, Christopher. «Aristotle». En Edward N. Zalta, ed. Stanford Encyclopedia of Philosophy (en inglés) (Winter 2009 Edition).
  3. Mosterín, 2006, p. 155.
  4. «Apódeixis - Encyclopaedia Herder». encyclopaedia.herdereditorial.com. Consultado el 5 de abril de 2021.
  5. Véase la sección «The Subject of Logic: Syllogisms» en Smith, Robin. «Aristotle's Logic». En Edward N. Zalta, ed. Stanford Encyclopedia of Philosophy (en inglés) (Winter 2009 Edition).
  6. Primeros analíticos, 24b 20.
  7. Véase la sección «Aristotelian Deductions and Modern Valid Arguments» en Smith, Robin. «Aristotle's Logic». En Edward N. Zalta, ed. Stanford Encyclopedia of Philosophy (en inglés) (Winter 2009 Edition).
  8. Véase la sección «The Syllogistic» en Smith, Robin. «Aristotle's Logic». En Edward N. Zalta, ed. Stanford Encyclopedia of Philosophy (en inglés) (Winter 2009 Edition).
  9. Ponsatí-Murlà, 2015, pp. 138-142.
  10. En los Primeros analíticos véase la parte 4 del libro 1 para la primera figura, la parte 5 para la segunda, y la parte 6 para la tercera (versión en inglés).
  11. Barnes, Jonathan, 1942-. The Cambridge companion to Aristotle (1st ed edición). ISBN 0521411335. OCLC 29753145. Consultado el 24 de mayo de 2019.
  12. Aristotle. (2009). Prior analytics. Book 1. Clarendon Press. ISBN 9780199250417. OCLC 300721020. Consultado el 24 de mayo de 2019.
  13. «Illiniois Medieval Association - EMS». ima.wildapricot.org. Consultado el 24 de mayo de 2019.
  14. Lagerlund, Henrik. (2000). Modal syllogistics in the Middle Ages. Brill. ISBN 9004116265. OCLC 43334300. Consultado el 24 de mayo de 2019.
  15. Ebbesen, Sten. (2008). Greek-Latin philosophical interaction. Ashgate Pub. ISBN 9780754658375. OCLC 85692826. Consultado el 24 de mayo de 2019.

Enlaces externos
  • Probo (filósofo sirio): Tratado sobre los "Primeros analíticos" de Aristóteles.
    • Texto francés, con anotaciones en este idioma, en el sitio de Philippe Remacle: trad. de Albin van Hoonacker (1857 - 1933); Imprimerie Nationale, París, 1900.
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.