Conjunto independiente
En teoría de grafos, un conjunto independiente o estable es un conjunto de vértices en un grafo tal que ninguno de sus vértices es adyacente a otro. Es decir, es un conjunto V de vértices tal que para ningún par de ellos existe alguna arista que los conecten. En otras palabras, cada arista en el grafo contiene a lo más un vértice en V. El tamaño de un conjunto independiente es el número de vértices que contiene.
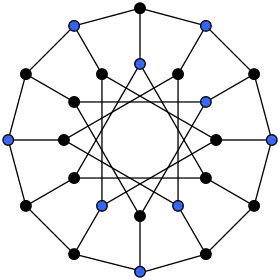
Un conjunto independiente maximal[nota 1] es un conjunto independiente tal que añadiendo cualquier otro vértice al conjunto, este deja de ser independiente.
Definición formal
Dado un grafo G, un subconjunto de vértices H ⊂ V(G) se llama conjunto independiente si no hay dos vértices en H que sean adyacentes.
El número de independencia de G es el tamaño de un conjunto independiente más grande, y se denota por α(G).[1]
Computabilidad
El conjunto independiente máximo corresponde al mayor conjunto independiente definible sobre un grafo dado. El problema de encontrar un conjunto con estas características se llama problema del máximo conjunto independiente y es NP-completo, por lo cual es poco probable que exista un algoritmo que lo resuelva eficientemente.
El problema de decidir si un grafo dado tiene un conjunto independiente de un tamaño particular es el Problema del conjunto independiente, el cual es computacionalmente equivalente a decidir si un grafo tiene un clique de un tamaño particular. Esto porque, si un grafo tiene un conjunto independiente de tamaño k, luego su grafo complemento tendrá un clique de tamaño k. El problema de decisión del conjunto independiente (al igual que el problema del clique) también es NP-completo.
Véase también
- Matching (conjunto de aristas independientes)
Notas
- «Conjunto independiente maximal» no debe confundirse con el «máximo conjunto independiente». El primero es un conjunto independiente que no está contenido en ningún otro conjunto independiente mayor que él. En efecto, el problema de encontrar un conjunto independiente maximal puede resolverse en tiempo polinomial mediante un simple algoritmo voraz.[cita requerida]
Referencias
- Scheinerman: Matemáticas discretas ISBN 970-686-071-1
Enlaces externos
- Weisstein, Eric W. «MaximalIndependentVertexSet». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Pruebas de testing (benchmarks) para problemas del Clique máximo, Máximo conjunto independiente, Mínima cobertura de vértices y Coloreo de vértices Archivado el 29 de mayo de 2013 en Wayback Machine.
| Control de autoridades |
|
|---|
Datos: Q1060343
Multimedia: Independent set (graph theory) / Q1060343