Proyección cónica
En matemática, concretamente en geometría, una proyección cónica es el sistema de representación gráfico en donde un haz de rectas proyectantes que confluyen en un punto —el ojo del observador—,[1] proyectan el cuerpo como una imagen sobre el plano auxiliar que intercepta dichas rectas.
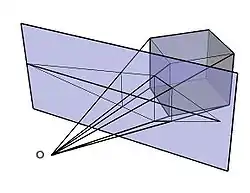
Este sistema de representación reproduce fielmente en un plano las imágenes del espacio, con un resultado muy similar a como lo percibimos realmente.
Es el sistema empleado en la perspectiva cónica.
Elementos
- Plano auxiliar: plano donde se proyectan las imágenes como un papel, un lienzo o una pantalla.
- Ojo del observador: lugar desde el que se observa el plano auxiliar, también llamado centro de proyección.
- Punto de fuga: punto del plano auxiliar en el que concurren todas las proyecciones de las rectas paralelas.
Construcciones
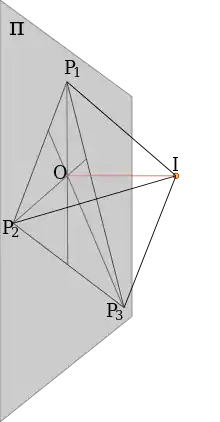
La construcción de los puntos de fuga y probar su adecuada situación en el plano de proyección se diferencian nominalmente según la geometría con la que se plantee ya sea la geometría clásica como la geometría proyectiva.
Geometría euclídea
Premisas generales:
- De las rectas paralelas entre sí y al plano auxiliar se dice que sus proyecciones sobre el plano tienen un punto de fuga en el infinito y que por tanto dichas proyecciones son paralelas.
- Si las rectas paralelas entre sí no son paralelas al plano auxiliar, entonces se genera un punto de fuga, , en la que aparentemente concurren todas las proyecciones de dichas rectas.
Todo ojo de observador, , proyecta un punto, , con la perpendicular al plano auxiliar .
Ejemplo
Un cubo o cualquier ortoedro tiene rectas paralelas en 3 direcciones distintas, por tanto tiene 3 puntos de fuga .
- Cuando coincide con se genera la perspectiva con un único punto de fuga ya que los otros dos están en el infinito(fuera del campo visual del observador).
- Cuando está situado en la recta que determinan dos puntos de fuga entonces el tercero está en el infinito.
- En el caso en el que los tres puntos de fuga no estén en el infinito, entonces es el ortocentro del triángulo descrito por los tres puntos de fuga.
 Perspectiva con un único punto de fuga.
Perspectiva con un único punto de fuga.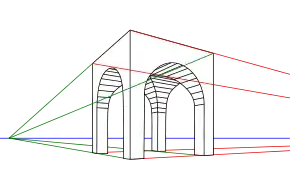 Perspectiva con dos puntos de fuga.
Perspectiva con dos puntos de fuga. Perspectiva con tres puntos de fuga.
Perspectiva con tres puntos de fuga.
Para construir otros ángulos necesarios para proporcionar un cubo, como el de 45°:
- Partiendo de un punto de fuga se trabaja sobre el plano abatido directamente sobre el plano solo cuando el otro punto de fuga pertenece a la recta PO (estos dos planos son perpendiculares).
- Partiendo de dos puntos de fuga al azar el plano a abatir es el y por lo tanto requiere técnicas de diédrico.
Ejemplo

Véase también
|
Referencias
- Real Academia Española. «proyección cónica». Diccionario de la lengua española (23.ª edición).