Perspectiva cónica

Utilizada en arquitectura e interiorismo para representar edificios y volúmenes. Es la que más se aproxima a la visión real, y equivale a la imagen que observamos al mirar un objeto con un solo ojo. Nos permite percibir una profundidad espacial parecida a la visión estereoscópica.

Los programas informáticos realizan simulaciones gráficas generando imágenes planas mediante algoritmos de carácter geométricos. Es común que a la vez combinen el renderizado de superficies y texturas, dando a la imagen final un aspecto fotorrealista.

Es frecuente su empleo en carteles de complejos y edificaciones inmobiliarias que están en construcción, ya que muestra de una forma realista como será la nueva obra.

La ciudad ideal (1475), Piero della Francesca.

Perspectiva cónica.

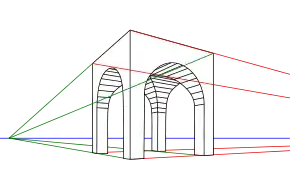
En la construcción geométrica de las perspectivas cónicas[1] se pueden encontrar dos métodos. El primero, que podría denominarse “método proyectivo”, se basa en un sistema de proyección cónica, inspirado en el sistema óptico visual. El segundo, es el “método directo”. En este caso se trabaja directamente sobre la imagen atendiendo a diferentes condiciones geométricas que se denominan “leyes perspectivas”. Este método, emparentado con la observación del natural, también debe cumplir condiciones geométricas de trazado, si se quiere realizar una expresión coherente y exacta del espacio representado.[2]

Procedimientos proyectivos

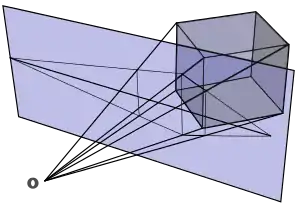
Se denominan así, porque recurren a una representación de los volúmenes en el espacio en el sistema diédrico de la geometría descriptiva, sobre el cual se aplica un segundo sistema de proyección cónica. El centro de dicha proyección es el punto de vista (observador) y el plano sobre el cual se proyecta es el plano del dibujo, comúnmente denominado plano del cuadro. Para que en las proyecciones cónicas se logren imágenes semejantes a las visuales, el espacio de proyección se limita a una zona denominada cono de visión. Básicamente se pueden distinguir dos procedimientos proyectivos, y un tercero que es la combinación de los dos primeros.

Procedimiento de las proyectantes visuales

Consiste en proyectar desde el punto de vista (observador) cada uno de los vértices del modelo, hasta el PC (plano del cuadro). En dicho plano, los vértices proyectados de cada arista se unen, obteniendo así la imagen perspectiva de los objetos. Para hallar la intersección de cada visual (o proyectante) en el PC, se utilizan planos que las contengan. Por ello este procedimiento también puede denominarse “de los planos visuales”.

Procedimiento de las prolongaciones

Consiste en prolongar las aristas de los objetos, principalmente las horizontales, y hallar sus perspectivas. Para trazar las perspectivas de las prolongaciones (rectas), se halla la perspectiva del punto en común de todas las aristas paralelas, que es el punto impropio, ubicado en el infinito –como se sabe-, pero que en la proyección cónica tiene su representación en el PC. La perspectiva del punto impropio, es el punto de fuga de las aristas paralelas. Para cada recta se halla un segundo punto: su intersección con el plano del cuadro. La unión del punto de fuga con la intersección, es la perspectiva de la recta. Por último, las intersecciones de las rectas perspectivas que contienen a las aristas, determinan los vértices, obteniendo así la imagen de los cuerpos.

Una variación

Del procedimiento anterior, es hallar cada vértice, con las perspectivas de rectas auxiliares que los contengan. En lugar de prolongar aristas, se usan rectas en otras direcciones, con el propósito de que los puntos de fuga no queden tan retirados del cuadro, en donde se construye el modelo.

Procedimiento combinado

Consiste en prolongar aristas solo hacia uno de los lados, generalmente el que posibilita la obtención del punto de fuga más próximo, y por proyectantes visuales, hallar sobre las rectas prolongadas ya en perspectiva, los vértices de los objetos. Este, o cualquiera de los procedimientos proyectivos, necesitan de al menos una proyección ortogonal de los volúmenes que se van a representar, y las proyecciones en el diedro del punto de vista (observador).

Método directo

Posibilita la construcción de perspectivas, trabajando directamente sobre la imagen. No necesita la representación espacial diédrica. En su defecto, utiliza propiedades geométricas que comúnmente se conocen como “reglas perspectivas”. Este método, también puede ser muy exacto, aún sin tener las representación en proyecciones. Presenta algunas ventajas, como por ejemplo la posibilidad de hallar perspectivas de cuerpos grandes a distancias lejanas en una misma solución con elementos pequeños a distancias cercanas. Con los procedimientos proyectivos, estas diferencias de escalas serían de difícil representación en el sistema diédrico. El método directo, permite al artista, desprenderse de trazados engorrosos, dejando que su intuición visual – espacial predomine en la búsqueda de vistas interesantes.

Perspectiva paralela o frontal: Es en la que se utiliza un único punto de fuga, que coincide con el punto principal.

Perspectiva oblicua de 2 puntos: Se emplean dos puntos de fuga, localizados sobre la línea de horizonte. Se pueden ver 2 caras del cubo.

Perspectiva aérea: Utiliza tres puntos de fuga. Cuando el horizonte es muy alto o muy bajo, las líneas se alteran por la perspectiva y se necesita un tercer punto exterior en una línea de horizonte (vertical) accesoria.

Ejemplo

Vista tridimensional de los elementos que intervienen en la realización de una perspectiva cónica: el modelo a representar (a la izquierda); el plano del dibujo, en el centro; y el punto de vista (a la derecha)

Elementos gráficos de una perspectiva cónica: planta y alzado del modelo a representar en coordenadas, incluyendo la posición relativa del punto de vista (abajo); y traslación de la proyección de las visuales al plano del dibujo (arriba)

Como se ha visto en párrafos anteriores, existen numerosos procedimientos gráficos para dibujar una perspectiva cónica, en los que se puede jugar libremente con el aspecto final de la representación prefijando de antemano determinados puntos de fuga, lo que implícitamente presupone adecuar arbitrariamente las posiciones relativas entre el modelo a representar, el plano del dibujo y el punto de vista.[3]

Sin embargo, cuando se dispone de las coordenadas cartesianas tanto del modelo a representar como del punto de vista y del plano del dibujo (circunstancia que es la habitual en los modelos tridimensionales de representación gráfica por ordenador), es relativamente sencillo dibujar la perspectiva cónica de cualquier modelo a partir de su representación diédrica, en la que también se incluyan las posiciones del plano del dibujo y del punto de vista.

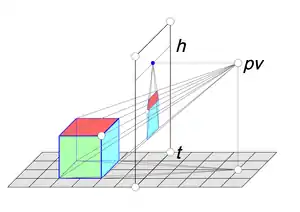
En el ejemplo adjunto, se representa la perspectiva cónica de un cubo apoyado sobre una cuadrícula horizontal. En la vista tridimensional se aprecia la posición relativa de los elementos que intervienen en el dibujo:

• A la izquierda aparece el modelo (el cubo a representar)
• En el centro se sitúa el plano del dibujo (la superficie donde se dibujará la perspectiva)
• A la derecha aparece el punto de vista (la posición desde la que se observa el modelo)

Dado que se está trabajando en un sistema de coordenadas concreto (el que define las vistas diédricas en planta y alzado del modelo), se asumen implícitamente los planos verticales y horizontales definidos por este sistema de coordenadas. En este caso, el plano del dibujo es paralelo al plano vertical de la proyección diédrica, aunque podría no serlo. Esta disposición condiciona a su vez la posición de la línea del horizonte del dibujo (h) y de la línea del terreno (t), ligadas a su vez a la posición relativa del plano del dibujo y del punto de vista.

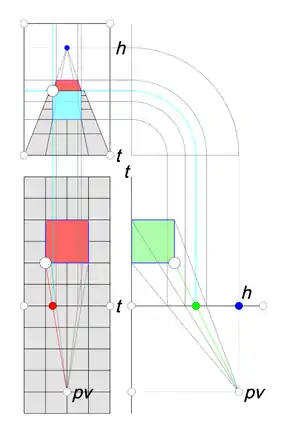
En el diagrama de la derecha se detallan los elementos gráficos que intervienen en el procedimiento general para representar cualquier punto del modelo en una perspectiva cónica:

• En primer lugar, deben prepararse las vistas diédricas del modelo (planta y alzado), situando en ambas el punto de vista y el plano del dibujo. El caso más sencillo es el incluido en el diagrama, cuando el plano del dibujo de la cónica es perpendicular al plano del alzado. Esto permite utilizar directamente la planta y el alzado diédricos del modelo para dibujar la cónica. En caso contrario, sería necesario redibujar el alzado del modelo a partir de la planta, según una vista proyectada ortogonalmente sobre un plano vertical perpendicular al plano del dibujo.
• Una vez dispuestos estos elementos gráficos, para hallar la posición de cualquier punto del modelo en la perspectiva cónica, basta con trasladar las proyecciones horizontal y vertical al dibujo, cuya intersección determina la posición buscada. Así, por ejemplo, para determinar la posición en la cónica de la esquina superior izquierda del cubo (marcada con un círculo blanco), se determinan:

• Su proyección horizontal respecto al plano del dibujo (el punto rojo sobre la línea t, obtenido como corte de la visual roja que une el punto de vista con el vértice del cubo en planta)
• Su proyección vertical respecto al plano del dibujo (el punto verde sobre la línea t-h, obtenido como corte de la visual verde que une el punto de vista con el vértice del cubo en alzado)

• Mediante las líneas auxiliares de color cyan, se llevan estas posiciones al plano del dibujo (directamente las distancias horizontales, y giradas 90° las distancias verticales). La intersección de ambas determina la posición buscada del vértice del cubo sobre el dibujo.
• Repitiendo este procedimiento, se puede determinar la posición sobre la cónica de cualquier punto del modelo. Dado que los segmentos rectilíneos del modelo siguen siendo rectos en el dibujo, basta calcular la posición de los vértices del cubo para poder representar sus aristas.

Como se puede observar, el punto de fuga en el que convergen las aristas laterales del cubo aparece espontáneamente, como consecuencia de la posición relativa entre el modelo, el plano del dibujo y el punto de vista. Este procedimiento gráfico es prácticamente el mismo que se utiliza analíticamente para calcular perspectivas por ordenador, determinando la posición de la proyección de los puntos del modelo sobre el plano del dibujo como la intersección de tres planos: el propio plano del dibujo; un plano vertical que pasa por el punto de vista y el punto del modelo; y un tercer plano paralelo a la línea del horizonte que contenga a ambos.[3]

Un método sencillo para calcular y comparar proporciones, sobre todo distancias verticales y horizontales, consiste en usar un lápiz como regla. Seleccionamos el objeto que queremos usar como parámetro para nuestro dibujo y luego tomamos un lápiz con la punta para arriba, sin olvidarnos de sostener el brazo bien estirado. Alineamos la punta del lápiz con la parte superior del objeto y el dedo con la parte inferior.[4] Esta medición nos permitirá calcular proporcionalmente los otros objetos. Hemos de estar seguros de que el lápiz se encuentre en posición totalmente vertical a la hora de medir profundidades. Para calcular el grado de inclinación o para medir horizontalmente, el lápiz habrá de estar perpendicular a la línea de visión.

• Empezaremos con el lápiz en posición horizontal y luego lo giraremos hasta que se encuentre sobre la línea. Así se determinará el ángulo. Trabajar midiendo a ojo es una técnica muy útil. El diagrama muestra cómo funciona este sistema para emprender un bodegón de un cubo sobre una mesita.

• Si somos diestros, tendremos que mirar por el lado izquierdo del tablero de dibujo, de modo que la mano que dibuja no interfiera con las líneas de mira, perturbando la visión. Con el tablero en posición vertical y con un ojo cerrado, moveremos la cabeza ligeramente hacia la izquierda y hacia la derecha, hasta lograr que el borde del tablero pueda utilizarse como plomada para determinar el tamaño de cada parte de los objetos y, luego, marcaremos estos puntos en el borde del tablero. Esto es particularmente útil para dibujar figuras, pero también puede utilizarse con buenos resultados para dibujar paisajes o, como en este caso, una naturaleza muerta. Es un método consagrado, como lo demuestran las marcas en el borde de muchos dibujos de grandes maestros, lo cual demuestra que dibujaban midiendo a ojo.

Perspectiva a mano alzada. Boceto de Leonardo da Vinci.

• Percibimos los objetos en un plano perpendicular a nuestra línea de visión. Al mirar de frente, el plano será vertical, como si hubiera un cristal suspendido frente a nosotros. Sin embargo, cuando dibujamos, el tablero puede estar inclinado, sobre las rodillas o sobre un caballete, de manera que hemos de mirar hacia abajo y, no obstante, tendemos a visualizar un plano vertical delante de nuestros ojos. Para traducir esta imagen vertical a un tablero colocado en cierto ángulo, debemos ajustar mentalmente las proporciones, cosa esta que, sin duda, resulta compleja. Corremos el riesgo de ajustar en exceso, haciendo demasiado grande la parte inferior de lo que estamos dibujando. Probablemente para un principiante resulte más fácil utilizar el tablero vertical, mientras va adquiriendo más práctica y experiencia.

• Existe una excepción natural al uso del tablero vertical, que es cuando se dibuja un tema horizontal (por ejemplo, una naturaleza muerta o un paisaje). En esos casos, es mucho más fácil mirar por encima de la parte superior.

• Cámara oscura

• Beltrán, J. M. (2008). Sistema diédrico y perspectivas. Universidad de Granada. ISBN 9788433848864.
• Gómez-Pompa Pérez, Mónica; Herrero del Cura, Sofía. Perspectiva Cónica,. ISBN 978-84-605-7731-7.
• Izquierdo Asensi, F. (2008). Geometría descriptiva I: Sistemas y perspectivas.
• Revilla Blanco, F. Javier (2007). Geometría descriptiva. Sistema de perspectiva cónica. Donostiarra. ISBN 9788470630507.