Relación euclidiana
En matemáticas, las relaciones euclidianas son una clase de relación binarias que formalizan "Axioma 1" en Elementos de Euclides': "Magnitudes que son iguales a la misma son iguales entre sí".
Definición
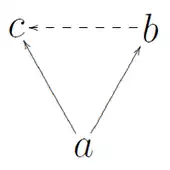
Propiedad euclidiana derecha: las flechas sólidas y discontinuas indican los antecedentes y los consecuentes, respectivamente.
Una relación binaria R sobre un conjunto X es euclídea (a veces llamada euclídea derecha) si satisface lo siguiente: para cada a, b, c en X, si a está relacionada con b y c, entonces b está relacionada con c. [1] Para escribir esto en lógica de predicados:
A su vez, una relación R en X es euclídea de izquierda si para cada a, b, c en X, si b está relacionada con a y c está relacionada con a, entonces b está relacionada con c:
Propiedades
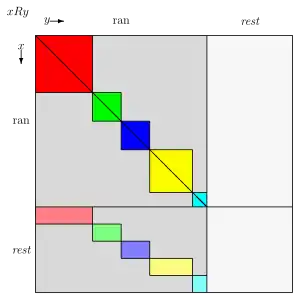
Relación euclidiana derecha esquematizada según la propiedad 10. Los cuadrados de color intenso indican las clases de equivalencia de RPlantilla:Prime. Rectángulos de color pálido indican las posibles relaciones de los elementos en X\ran(R). En estos rectángulos, las relaciones pueden, o no, mantener.
- Debido a la conmutatividad de ∧ en el antecedente de la definición, aRb ∧ aRc implica incluso bRc ∧ cRb cuando R es euclídea derecha. Del mismo modo, bRa ∧ cRa implica bRc ∧ cRb cuando R es euclídea izquierda.
- La propiedad de ser euclidiano es diferente de transitividad. Por ejemplo, ≤ es transitiva, pero no euclídea derecha,[2] mientras que xRy definida por 0 ≤ x ≤ y + 1 ≤ 2 no es transitiva,[3] sino euclídea derecha en número naturals.
- Para relación simétricas, la transitividad, la euclidiana derecha y la euclidiana izquierda coinciden. Sin embargo, también una relación no simétrica puede ser a la vez transitiva y euclidiana derecha, por ejemplo, xRy definida por y=0.
- Una relación que es a la vez euclídea derecha y reflexiva es también simétrica y, por tanto, una relación de equivalencia.[1][4] Análogamente, cada relación euclídea izquierda y reflexiva es una equivalencia.
- La rango de una relación euclídea derecha es siempre un subconjunto[5] de su dominio. La restricción de una relación euclídea derecha a su rango es siempre reflexiva,[6] y por lo tanto una equivalencia. Análogamente, el dominio de una relación euclídea izquierda es un subconjunto de su rango, y la restricción de una relación euclídea izquierda a su dominio es una equivalencia. Por tanto, una relación euclídea derecha sobre X que sea también total derecha (respectivamente una relación euclídea izquierda sobre X que sea también total izquierda) es una equivalencia, ya que su rango (respectivamente su dominio) es X. [7]
- Una relación R es a la vez euclídea izquierda y derecha, si, y sólo si, el conjunto dominio y el conjunto rango de R coinciden, y R es una relación de equivalencia sobre ese conjunto.[8]
- Una relación euclidiana derecha es siempre cuasitransitiva,[9] como es una relación euclídea izquierda.[10].
- Una relación euclídea derecha connected siempre es transitiva;[11] y por tanto es una relación euclídea izquierda conexa.[12]
- Si X tiene al menos 3 elementos, una relación euclídea derecha conexa R sobre X no puede ser antisimétrica,[13] y tampoco puede una relación euclidiana izquierda conectada en X.[14] En el conjunto de 2 elementos X = { 0, 1 }, e. g. la relación xRy definida por y=1 es conexa, euclídea derecha y antisimétrica, y xRy definida por x=1 es conexa, euclídea izquierda y antisimétrica.
- Una relación R sobre un conjunto X es euclídea derecha si, y sólo si, la restricción RPlantilla:Prime := R|ran(R) es una equivalencia y para cada x en X\ran(R), todos los elementos con los que x está relacionada bajo R son equivalentes bajo RPlantilla:Prime.[15] Análogamente, R en X es euclídea izquierda si, y sólo si, RPlantilla:Prime := R|dom(R) es una equivalencia y para cada x en X\dom(R), todos los elementos que están relacionados con x bajo R son equivalentes bajo RPlantilla:Prime.
- Una relación euclidiana izquierda es izquierda-única si, y sólo si, es antisimétrica. Análogamente, una relación euclídea derecha es única derecha si, y sólo si, es antisimétrica.
- Una relación euclídea izquierda y única izquierda es transitiva vacua, y también lo es una relación euclídea derecha y única derecha.
- Una relación euclídea izquierda es cuasi-reflexiva izquierda. Para las relaciones únicas por la izquierda, la inversa también es válida. A su vez, cada relación euclidiana derecha es cuasi-reflexiva derecha, y cada relación única derecha y cuasi-reflexiva derecha es euclidiana derecha.[16]
Referencias
- Fagin, Ronald (2003), Reasoning About Knowledge, MIT Press, p. 60, ISBN 978-0-262-56200-3..
- e.g. 0 ≤ 2 y 0 ≤ 1, pero no 2 ≤ 1
- e.g. 2R1 y 1R0, pero no 2R0
- xRy y xRx implica yRx.
- La igualdad de dominio y rango no es necesaria: la relación xRy definida por y=min{x,2} es euclídea derecha sobre los números naturales, y su rango, {0,1,2}, es un subconjunto propio de su dominio de los números naturales.
- Si y está en el rango de R, entonces xRy ∧ xRy implica yRy, para algún x adecuado. Esto también demuestra que y está en el dominio de R.
- Buck, Charles (1967), «Una definición alternativa para las relaciones de equivalencia», The Mathematics Teacher 60: 124-125..
- El sentido sólo si se deduce del párrafo anterior. Para el sentido si, supongamos aRb y aRc, entonces a, b, c son miembros del dominio y del rango de R, por tanto bRc por simetr'ıa y transitividad; la euclidiana izquierda de R se deduce de forma similar.
- Si xRy ∧ ¬yRx ∧ yRz ∧ ¬zRy se cumple, entonces tanto y como z están en el rango de R. Como R es una equivalencia en ese conjunto, yRz implica zRy. Por tanto, el antecedente de la fórmula de definición de cuasi transitividad no puede satisfacerse.
- Un argumento similar se aplica, observando que x, y están en el dominio de R.
- Si xRy ∧ yRz se cumple, entonces y y z están en el dominio de R. Como R es conexo, xRz o zRx o x=z se cumple. En el caso 1, no queda nada por demostrar. En los casos 2 y 3, también x está en el intervalo. Por tanto, xRz se deduce de la simetría y reflexividad de R sobre su rango, respectivamente.
- Similar, usando que x, y están en el dominio de R.
- Dado que R es conexa, al menos dos elementos distintos x, y están en su rango, y xRy ∨ yRx se cumple. Puesto que R es simétrica en su rango, incluso xRy ∧ yRx se cumple. Esto contradice la propiedad de antisimetría.
- Por un argumento similar, utilizando el dominio de R.
- Sólo si: R{prime}} es una equivalencia como se muestra arriba. Si x∈X\ran(R) y xRPlantilla:Primey1 y xR{prime}}y2, entonces y1Ry2 por derecho euclidiano, por lo tanto y1RPlantilla:Primey2. — Si: si xRy ∧ xRz se cumple, entonces y,z ∈ran(R). En el caso también x∈ran(R), incluso xRPlantilla:Primey ∧ xRPlantilla:Primez se cumple, por lo tanto yRPlantilla:Primez por simetría y transitividad de RPlantilla:Prime, por lo tanto yRz. En el caso de que x∈X\ran(R), los elementos y y z deben ser equivalentes bajo RPlantilla:Prime por suposición, de ahí también yRz.
- Jochen Burghardt (Nov 2018), Leyes sencillas sobre propiedades no predominantes de relaciones binarias (Informe técnico), arXiv:1806.05036v2. Lemma 44-46.
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.