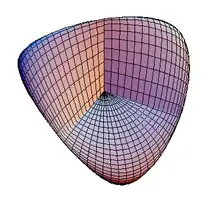
Superficie de Steiner
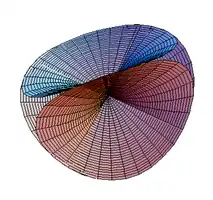
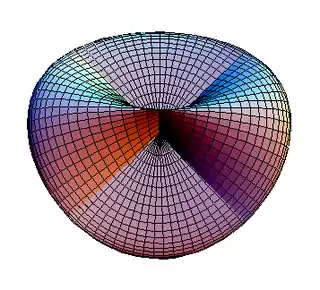
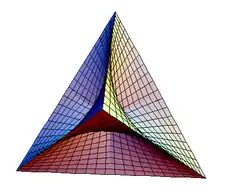
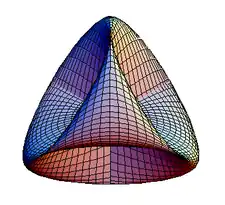
La superficie de Steiner, descubierta en 1844 por el matemático suizo Jakob Steiner, es una inmersión auto-intersecante del plano proyectivo real en el espacio tridimensional, con un grado de simetría inusualmente alto. Se trata de una superficie de cuarto grado, con la particularidad de que cada uno de sus planos tangentes se cruza con la superficie en un par de cónicas.[1]

Historia
El matemático suizo Jakob Steiner (1796-1863) descubrió este tipo de superficies en 1844 durante un viaje a Roma, por lo que también se suele conocer como superficie romana. Steiner nunca publicó sus descubrimiento, y sería su colega, el matemático alemán Karl Weierstrass (1815-1897), quien publicaría un artículo con los resultados de Steiner en 1863, en el mismo año de la muerte del matemático suizo.[1]
Existen diez tipos de superficies de Steiner (clasificados por Coffman, Schwartz y Stanton) entre los que se encuentran la gorra cruzada y la propia superficie romana de Steiner.[2]
Construcción
| ||
| ||
|
La construcción más simple es la imagen de una esfera centrada en el origen bajo la acción de la función . Esto lleva a la fórmula implícita:
Además, al parametrizar la esfera en términos de longitud () y latitud (), se obtienen las siguientes ecuaciones paramétricas para la superficie romana:
El origen es un punto triple, y cada uno de los planos. , , , es tangente a la superficie en este punto. Los otros lugares de la auto-intersección son puntos dobles, que definen segmentos a lo largo de cada eje coordenado y terminan en seis puntos de aplastamiento. El grupo de simetría de la superficie es el del tetraedro. Más específicamente, son proyecciones lineales de una inmersión en un espacio de 5 dimensiones, llamada superficie de Veronese, que es la imagen de una esfera regular centrada en el origen.
Una superficie de Steiner es un polinomio cuadrático en variables de una superficie dada en espacio tridimensional:
Construcción: dado el espacio proyectivo real, considérense las coordenadas homogéneas en el espacio proyectivo de 5 dimensiones, con coordenadas homogéneas:
Deducción de la fórmula implícita
Por simplicidad se considerara solo el caso para . Se traza la esfera identificada por los tres puntos tal que
Ahora se aplica la transformación a estos puntos , donde
De esta manera, se obtiene que
y por lo tanto , que es la expresión buscada.
Deducción de las ecuaciones paramétricas
La superficie romana viene dada por:[3]
En coordenadas cartesianas, se tiene que:
Otros parámetros de la ecuación están dados por:
Ahora, considérese una esfera de radio , cuya superficie se expresa según su longitud y latitud . Entonces, sus ecuaciones paramétricas son
Entonces, aplicando la transformación en todos los puntos de esta esfera, se obtiene
que son los puntos de la superficie de Steiner. Se tiene que vale entre y , y que varía entre y .
De la parametrización de la esfera unitaria
bajo la transformación
La gorra cruzada (o bonete) viene dada por:[4]
En coordenadas cartesianas:
Relación con el plano proyectivo real
El resultado de la aplicación que genera la superficie no es una inmersión del plano proyectivo; sin embargo, la figura resultante de la eliminación de seis puntos singulares sí lo es.
Antes de transformarse, la esfera no es homeomorfa con el plano proyectivo real , mientras que la esfera centrada en el origen sí posee esta propiedad: es decir, si los puntos pertenecen a la esfera, sus antipodales pertenecen a la misma esfera, pero los dos tripletes de coordenadas son diferentes y están ubicados en lados opuestos con respecto al centro de la esfera.
La transformación convierte los dos tripletes de puntos antipodales, en el punto
Véase también
Referencias
- «Steiner surface». Encyclopedia Britannica (en inglés). Consultado el 16 de marzo de 2020.
- Marco Fulvio Barozzi. «Sinisgalli e il Carciopholus romanus». Consultado el 13 luglio 2015.
- «ROMAN SURFACE». mathcurve.com (en inglés). Consultado el 16 de marzo de 2020.
- «CROSS-CAP». mathcurve.com (en inglés). Consultado el 16 de marzo de 2020.
Enlaces externos
 Wikimedia Commons alberga una categoría multimedia sobre Superficie de Steiner.
Wikimedia Commons alberga una categoría multimedia sobre Superficie de Steiner.- «Conversione di una Superficie romana di Steiner in una Superficie di Boy». Archivado desde el original el 9 de diciembre de 2006. Consultado el 16 de marzo de 2020.
- A. Coffman, "Steiner Surfaces"
- Weisstein, Eric W. «Roman Surface». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Roman Surfaces at the National Curve Bank (website of the California State University)
- Ashay Dharwadker, Heptahedron and Roman Surface, Electronic Geometry Models, 2004.