Porcentaje

El porcentaje es un punto símbolo matemático que representa una cantidad dada como una fracción en 100 partes iguales. También se le llama comúnmente tanto por ciento, donde por ciento significa «de cada cien unidades». Se usa para definir las relaciones entre dos cantidades, de forma que el tanto por ciento de una cantidad, que es un número, se refiere a la parte proporcional que ese número de unidades representa por cada cien de esa cantidad.

Símbolo del porcentaje

El porcentaje se denota utilizando el símbolo «%»,[1] que matemáticamente equivale al factor 0,01 y que se debe escribir después del número al que se refiere, dejando un espacio de separación.[2][3] Por ejemplo, «treinta y dos por ciento» se representa escribiendo 32 %, y significa ‘treinta y dos de cada cien’. También puede representarse:

32\,\%=32\cdot 0{,}01

y, operando:

32\,\%=0{,}32

El 32 % de 2000 significa la parte proporcional a 32 unidades de cada 100 de esas 2000, es decir:

32\,\%\cdot 2000=0{,}32\cdot 2000=640

640 unidades en total.

El porcentaje se usa para comparar una fracción (que indica la relación entre dos cantidades) con otra, expresándolas mediante porcentajes para usar 100 como denominador común. Por ejemplo, si en un país hay 500 000 enfermos de gripe de un total de 10 millones de personas, y en otro hay 150 000 enfermos de un total de un millón de personas, resulta más claro expresar que en el primer país hay un 5 % (5 por ciento) de personas con gripe, y en el segundo hay un 15 % (15 por ciento), lo que da como resultado una proporción mayor en el segundo país.

Ejemplos

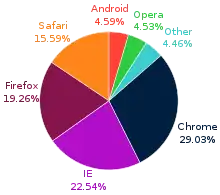
Un gráfico circular que muestra el porcentaje por navegador web que visita sitios de Wikimedia (abril de 2009 a 2012)

Por ejemplo, 45 % (léase "cuarenta y cinco por ciento") es igual a la fracción 45/100, la proporción 45:55 (o 45:100 cuando se compara con el total en lugar de la otra parte), o 0,45. Los porcentajes se utilizan a menudo para expresar una parte proporcional de un total.

(Del mismo modo, uno también puede expresar un número como una fracción de 1 000, usando el término "por mil" o el símbolo "‰".)

Ejemplo 1

Si el 50 % del número total de alumnos de la clase son hombres, eso significa que 50 de cada 100 alumnos son hombres. Si hay 500 estudiantes, entonces 250 de ellos son hombres.

Ejemplo 2

Un aumento de 0,15 € sobre un precio de 2,50 € es un aumento de una fracción de 0,15/2,50 = 0,06. Expresado como un porcentaje, esto es un aumento del 6 %.

Si bien muchos valores porcentuales están entre 0 y 100, no existe una restricción matemática y los porcentajes pueden tomar otros valores.[4] Por ejemplo, es común referirse a 111 % o −35 %, especialmente para cambios porcentuales y comparaciones.

Idea y origen

Ya era una herramienta de análisis en el siglo XV que tenía aplicación a la hora de calcular impuestos e intereses; sin embargo, el uso de este solo proviene de la abreviatura de una idea que databa desde hace mucho. En el antiguo imperio romano, el emperador Augusto estableció un sistema de impuestos en el que se dictaba que había que pagar el ${\textstyle {\frac {1}{100}}}$ sobre los bienes vendidos en subastas. Ya entonces, para facilitar los cálculos, utilizaban fracciones simplificadas a las centenas.

A medida que crecían las denominaciones de dinero en la Edad Media, los cálculos con un denominador de 100 se volvieron cada vez más estándar, de modo que desde finales del siglo XV hasta principios del siglo XVI, se hizo común que los textos aritméticos incluyeran tales cálculos. Muchos de estos textos aplicaron estos métodos a pérdidas y ganancias, tipos de interés y la regla de tres. En el siglo XVII, era estándar cotizar las tasas de interés en centésimas.[5]

Evolución

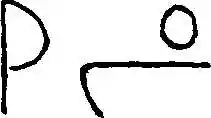
El primer símbolo que hacía referencia al «por ciento»

La idea de «por ciento» surge de la necesidad de abreviar el uso de las fracciones en la cotidianidad, pues resultaba tener mayor complejidad hacer referencia al ${\textstyle {\frac {2}{3}}}$ de una cantidad que al 66 %, por lo que, con el tiempo, era más común que se hablase únicamente de fracciones reducidas a las centenas, y progresivamente se fue actualizando la referencia hablada hasta llegar al «por ciento». Al hacerlo, nació la necesidad de plasmar la nueva abreviación, lo que generó, con el tiempo, el uso de varios símbolos. El primero provino de un manuscrito anónimo de 1425 en el que el autor hacía referencia al «por ciento» que se solía utilizar en la época con un símbolo que dio evolución al actual «%».

Cálculos

El valor porcentual se calcula multiplicando el valor numérico de la razón por 100. Por ejemplo, para hallar 50 manzanas como porcentaje de 1250 manzanas, primero se calcula la razón 50/1250 = 0,04, y luego se multiplica por 100 para obtener 4 %. El valor porcentual también se puede encontrar multiplicando primero en lugar de después, por lo que en este ejemplo, el 50 se multiplicaría por 100 para dar 5000, y este resultado se dividiría por 1250 para dar 4 %.

Para calcular un porcentaje de un porcentaje, se convierte ambos porcentajes a fracciones de 100, o a decimales, y se multiplican. Por ejemplo, 50 % de 40 % es:

50 / 100 \times 40 / 100 = 0,50 \times 0,40 = 0,20 = 20 / 100 = 20%.

No es correcto dividir por 100 y usar el signo de porcentaje al mismo tiempo; literalmente implicaría una división por 10.000. Por ejemplo, 25% = 25/100 = 0,25, no 25%/100, que en realidad es ²⁵⁄₁₀₀/100 = 0,0025. Un término como 100/100 % también sería incorrecto, ya que se leería como 1 por ciento, incluso si la intención fuera decir 100 %.

Siempre que se comunique sobre un porcentaje, es importante especificar a qué se refiere (es decir, cuál es el total que corresponde al 100 %). El siguiente problema ilustra este punto.

En cierta universidad, el 60 % de todos los estudiantes son mujeres, y el 10 % de todos los estudiantes son estudiantes de informática. Si el 5 % de las alumnas se especializan en ciencias de la computación, ¿qué porcentaje de estudiantes de ciencias de la computación son mujeres?

Se nos pide que calculemos la proporción de mujeres que se especializan en ciencias de la computación con respecto a todas las estudiantes de ciencias de la computación. Sabemos que el 60 % de todos los estudiantes son mujeres, y entre estos el 5 % son estudiantes de informática, por lo que concluimos que 60/100 × 5/100 = 3/100 o el 3 % de todos los estudiantes son mujeres con especialización en informática. Dividiendo esto por el 10 % de todos los estudiantes que son estudiantes de informática, llegamos a la respuesta: 3%/10% = 30/100 o el 30 % de todos los estudiantes de informática son mujeres.

Este ejemplo está estrechamente relacionado con el concepto de probabilidad condicional.

Símbolo

Muchos creen que el símbolo «%» ha evolucionado a partir de la expresión matemática ${\frac {x}{100}}.$

Símbolo en el siglo XV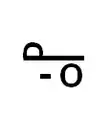
Símbolo en el siglo XVII
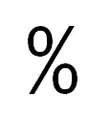Símbolo desde el siglo XVIII

El símbolo % es una forma estilizada de los dos ceros. Evolucionó a partir de un símbolo similar, sólo que presentaba una línea horizontal en lugar de diagonal (c. 1650), que a su vez proviene de un símbolo que representaba «P cento» (c. 1425), (per cento).[6][7] El "per" a menudo se abreviaba como "p", y finalmente desapareció por completo. El "cento" se contrajo a dos círculos separados por una línea horizontal, de la que se deriva el símbolo moderno "%".[8]

Otros símbolos relacionados incluyen ‰ (por mil) y ‱ (por diez mil, también conocido como un punto básico), que indican que un número se divide por mil o diez mil, respectivamente.

Representación

Tanto por ciento como fracción

El tanto por ciento se divide entre 100 y se simplifica la fracción.

Ejemplo:

Para saber cómo se representa el 10 % en fracción, se divide y luego se simplifica:

10\,\%={\cfrac {10}{100}}={\cfrac {1}{10}}=0,1

Tanto por ciento como multiplicación

La fracción común se multiplica por el número que sea necesario para que el denominador sea 100 y se toma el numerador, que será el porcentaje.

Ejemplo:

Para representar 1/10 como un porcentaje se hace la siguiente operación:

{\cfrac {1}{10}}={\cfrac {10}{100}}=10\,\%

Equivalencia entre un porcentaje y sus fracciones
¹⁄₁	⁹⁄₁₀	⁴⁄₅	³⁄₄	⁷⁄₁₀	²⁄₃	³⁄₅	¹⁄₂	²⁄₅	¹⁄₃	³⁄₁₀	¹⁄₄	¹⁄₅	³⁄₂₀	¹⁄₈	¹⁄₁₀	¹⁄₂₀	¹⁄₅₀	¹⁄₁₀₀	¹⁄₂₀₀
100 %	90 %	80 %	75 %	70 %	66,(6) %	60 %	50 %	40 %	33,(3) %	30 %	25 %	20 %	15 %	12,5 %	10 %	5 %	2 %	1 %	0,5 %

Obtener un tanto por ciento de un número

Para obtener un tanto por ciento de un número, simplemente se multiplica por 0,01, es decir, 1/100. Por ejemplo, el 25 % de 150 es $25\cdot 0,01\cdot 150=37,5$ . Una forma equivalente de tratar esta operación es considerar que se multiplica por la cifra y se divide por cien (pues 0,01 = 1/100).

Alternativamente, en un método muy habitual antaño, se construye una regla de tres simple directa. Así, para calcular el 25 % de 150, se hace la regla de tres: simplemente se multiplica cruzado y divide por el que queda solo o en conjunción con el restado.

\left.{\begin{array}{ccc}100\ \%&\longrightarrow &150\\25\ \%&\longrightarrow &x\end{array}}\right\}\to \quad x={\cfrac {150\cdot 25\ \%}{100\ \%}}=37,5

Por tanto: 37,5 es el 25 % de 150.

Porcentaje de aumento y disminución

Debido al uso inconsistente, no siempre está claro en el contexto a qué se refiere un porcentaje. Cuando se habla de una "subida del 10 %" o de una "bajada del 10 %" en una cantidad, la interpretación habitual es que es relativa al "valor inicial" de esa cantidad. Por ejemplo, si un artículo tiene un precio inicial de $200 y el precio aumenta un 10 % (un aumento de $20), el nuevo precio será de $220. Tenga en cuenta que este precio final es el 110 % del precio inicial (100 % + 10 % = 110 %).

Algunos otros ejemplos de cambios porcentuales:

Un incremento del 100 % en una cantidad significa que el importe final es el 200 % del importe inicial (100 % del inicial + 100 % de incremento = 200 % del inicial). En otras palabras, la cantidad se ha duplicado.
Un aumento del 800 % significa que la cantidad final es 9 veces la original (100 % + 800 % = 900 % = 9 veces mayor).
Una disminución del 60 % significa que el importe final es el 40 % del original (100 % – 60 % = 40 %).
Una disminución del 100 % significa que el importe final es "cero" (100 % – 100 % = 0 %).

En general, un cambio de $x$ por ciento en una cantidad da como resultado una cantidad final que es 100 + $x$ por ciento de la cantidad original (equivalentemente, (1 + 0.01 $x$ ) veces la cantidad original).

Porcentajes compuestos

Los cambios porcentuales aplicados secuencialmente no suman de la forma habitual. Por ejemplo, si el aumento del 10 % en el precio considerado anteriormente (en el artículo de 200€, elevando su precio a 220€) es seguido por una disminución del 10 % en el precio (una disminución de 22€), entonces el precio final será de 198€—no el precio original de 200€. La razón de esta aparente discrepancia es que los cambios del dos por ciento (+10 % y −10 %) se miden en relación con cantidades "diferentes" (200€ y 220€, respectivamente) y, por lo tanto, no se "cancelan".

En general, si un aumento de $x$ por ciento es seguido por una disminución de $x$ por ciento, y la cantidad inicial era $p$ , la cantidad final es $p$ (1 + 0,01 $x$ )(1 − 0.01 $x$ ) = $p$ (1 − (0.01 $x$ )Plantilla:Sup); por lo tanto, el cambio neto es una disminución general de $x$ por ciento de $x$ porcentaje (el cuadrado del cambio porcentual original cuando se expresa como un número decimal). Así, en el ejemplo anterior, después de un aumento y disminución de $x$ = 10 por ciento, el monto final, 198€, fue 10 % de 10 %, o 1 %, menos que el monto inicial de 200€. El cambio neto es el mismo para una disminución de $x$ por ciento, seguido de un aumento de $x$ por ciento; la cantidad final es $p$ (1 - 0,01 $x$ )(1 + 0,01 $x$ ) = $p$ (1 − (0,01 $x$ )Plantilla:Sup).

Esto se puede ampliar para un caso en el que uno no tenga el mismo cambio porcentual. Si la cantidad inicial $p$ conduce a un cambio porcentual $x$ , y el segundo cambio porcentual es $y$ , entonces la cantidad final es $p$ (1 + 0,01 $x$ )(1 + 0,01 $y$ ). Para cambiar el ejemplo anterior, después de un aumento de $x$ = 10 por ciento y disminución de $y$ = −5 percent, la cantidad final, 209€, es 4,5 % más que la cantidad inicial de 200€.

Como se muestra arriba, los cambios porcentuales se pueden aplicar en cualquier orden y tienen el mismo efecto.

En el caso de las tasas de interés, una forma muy común pero ambigua de decir que una tasa de interés subió del 10 % anual al 15 % anual, por ejemplo, es decir que la tasa de interés aumentó un 5 %, lo que teóricamente podría significar que aumentó del 10 % anual al 10,05 % anual. Es más claro decir que la tasa de interés aumentó en 5 puntos porcentuales (pp). La misma confusión entre los diferentes conceptos de porcentaje (edad) y puntos porcentuales puede potencialmente causar un gran malentendido cuando los periodistas informan sobre los resultados de las elecciones, por ejemplo, expresando tanto los resultados nuevos como las diferencias con los resultados anteriores como porcentajes. Por ejemplo, si un partido obtiene el 41 % de los votos y se dice que esto es un aumento del 2,5 %, ¿significa eso que el resultado anterior fue del 40 % (ya que 41 = 40 × (1 + 2,5/100)) o 38,5 % (desde 41 = 38,5 + 2,5)?

En los mercados financieros, es común referirse a un aumento de un punto porcentual (por ejemplo, del 3 % anual al 4 % anual) como un aumento de "100 puntos básicos".

Otros usos

La palabra "porcentaje" suele ser un nombre inapropiado en el contexto de las estadísticas deportivas, cuando el número al que se hace referencia se expresa como una proporción decimal, no como un porcentaje: "Shaquille O'Neal de los Phoenix Suns lideró la NBA con un .609 porcentaje de tiros de campo (FG%) durante la temporada 2008-09". (O'Neal acertó el 60,9 % de sus tiros, no el 0,609 %). Asimismo, el porcentaje de victorias de un equipo, la fracción de partidos que ha ganado el club, también suele expresarse como una proporción decimal; un equipo que tiene un porcentaje de victorias de .500 ha ganado el 50 % de sus partidos. La práctica probablemente esté relacionada con la forma similar en que se citan los promedios de bateo.

Como "porcentaje" se utiliza para describir la inclinación de la pendiente de una carretera o ferrocarril, cuya fórmula es 100 × subida/trayecto que también podría expresarse como la tangente del ángulo de inclinación por 100. Esta es la relación entre las distancias que un vehículo avanzaría vertical y horizontalmente, respectivamente, cuando sube o baja, expresado en porcentaje.

El porcentaje también se usa para expresar la composición de una mezcla por porcentaje en masa y porcentaje en moles.

Unidades relacionadas

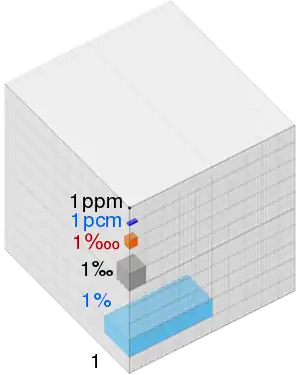
Visualización de 1 %, 1 ‰, 1 ‱, 1 pcm y 1 ppm como fracciones del bloque grande (versión más grande)

Diferencia de punto porcentual de 1 parte en 100
Por mil (‰) 1 parte en 1 000
Diferencia de punto base (bp) de 1 parte en 10,000
Pendiente (geografía)
Vuelta (ángulo)

Aplicaciones prácticas

Referencias

«Introduction to Percents». www.mathsisfun.com. Consultado el 28 de agosto de 2020.
«Aunque el símbolo % [...] se ve frecuentemente escrito sin separación de la cifra que lo precede, la norma establecida por la Oficina Internacional de Pesos y Medidas determina que se escribe precedido de un espacio». Citado en RAE y ASALE (2010). «La representación gráfica de las unidades léxicas: ortografía y otras normas de escritura». Ortografía de la lengua española. Madrid: Espasa Calpe. p. 590. ISBN 978-6-070-70653-0. Consultado el 5 de junio de 2017.
Antes de la Ortografía de 2010, la ASALE recomendó no dejar espacio (Sección Números del Diccionario panhispánico de dudas).
Fundéu BBVA (2011). Novedades de la Ortografía de la lengua española (2010). p. 7.
Bennett, Jeffrey; Briggs, William (2005), Using and Understanding Mathematics / A Quantitative Reasoning Approach (3rd edición), Pearson Addison Wesley, p. 134, ISBN 0-321-22773-5.
Smith, D.E. (1958) [1951]. History of Mathematics 2. Courier Dover Publications. pp. 247-249. ISBN 0-486-20430-8.
American Heritage Dictionary of the English Language, 3rd ed. (1992) Houghton Mifflin
«Definition of PERCENT». www.merriam-webster.com (en inglés). Consultado el 28 de agosto de 2020.
Smith p. 250

Véase también

partes por millón
por mil (‰) 1 parte en 1000
punto base 0,01 %
regla de tres

Enlaces externos

Wikcionario tiene definiciones y otra información sobre porcentaje.
Historia y origen de los porcentajes transcrita de historia de los porcentajes

Datos: Q11229
Multimedia: Percentages / Q11229
Libros y manuales: Porcentaje

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] «Introduction to Percents». www.mathsisfun.com. Consultado el 28 de agosto de 2020.

[2] «Aunque el símbolo % [...] se ve frecuentemente escrito sin separación de la cifra que lo precede, la norma establecida por la Oficina Internacional de Pesos y Medidas determina que se escribe precedido de un espacio». Citado en RAE y ASALE (2010). «La representación gráfica de las unidades léxicas: ortografía y otras normas de escritura». Ortografía de la lengua española. Madrid: Espasa Calpe. p. 590. ISBN 978-6-070-70653-0. Consultado el 5 de junio de 2017.
Antes de la Ortografía de 2010, la ASALE recomendó no dejar espacio (Sección Números del Diccionario panhispánico de dudas).

[3] Fundéu BBVA (2011). Novedades de la Ortografía de la lengua española (2010). p. 7.

[4] Bennett, Jeffrey; Briggs, William (2005), Using and Understanding Mathematics / A Quantitative Reasoning Approach (3rd edición), Pearson Addison Wesley, p. 134, ISBN 0-321-22773-5.

[5] Smith, D.E. (1958) [1951]. History of Mathematics 2. Courier Dover Publications. pp. 247-249. ISBN 0-486-20430-8.

[6] American Heritage Dictionary of the English Language, 3rd ed. (1992) Houghton Mifflin

[7] «Definition of PERCENT». www.merriam-webster.com (en inglés). Consultado el 28 de agosto de 2020.

[8] Smith p. 250