Teorema de Monge
En geometría, el teorema de Monge, nombrado así en referencia al matemático francés Gaspard Monge, establece que para cualquier grupo de tres círculos en un plano, ninguno de los cuales está completamente dentro de uno de los otros, los puntos de intersección de cada uno de los tres pares de líneas tangentes externas son colineales.
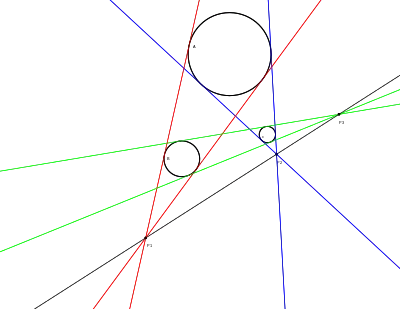
Para cualquier par de círculos en un plano, una tangente externa es una línea recta que es tangente a dos círculos pero que no pasa entre ellos. Hay dos líneas tangentes externas a dos círculos. Cada uno de estos pares tiene un punto de intersección único en el plano euclideo extendido. El teorema de Monge establece que los tres puntos dados por trío de círculos están siempre en línea recta. En el caso de que dos de los círculos sean del mismo tamaño, las dos líneas tangentes externas son paralelas. En este caso, el teorema de Monge afirma que los otros dos puntos de intersección deben estar en una línea paralela a esas dos tangentes externas. En otras palabras, si se considera que las dos tangentes externas se cruzan en el punto del infinito, los otros dos puntos de intersección deben estar en una línea que pasa por el mismo punto en el infinito, por lo que la línea entre ellos toma el mismo orientación que la tangente externa.
Demostración
La demostración más simple emplea una analogía tridimensional.[1] Hágase que los tres círculos se correspondan con tres esferas del mismo radio; los círculos corresponden a los ecuadores que resultan de un plano que pasa a través de los centros de las esferas. Las tres esferas se pueden intercalar de forma única entre dos planos. Cada par de esferas define un cono que es tangente externamente a ambas esferas, y el vértice de este cono corresponde al punto de intersección de las dos tangentes externas, es decir, el centro de homotecia externo. Dado que una generatriz del cono se encuentra en cada plano, el vértice de cada cono debe estar en ambos planos, y por lo tanto, en algún punto de la línea de intersección de los dos planos. Por lo tanto, los tres centros homotéticos externos son colineales.
El teorema de Monge también se puede demostrar mediante el uso del teorema de Desargues. Otra prueba sencilla utiliza el teorema de Menelao, ya que las relaciones se pueden calcular con los diámetros de cada círculo, que se eliminarán mediante formas cíclicas cuando se use el citado teorema.
El teorema de Desargues también afirma que 3 puntos de intersección de tangentes se encuentran sobre una recta, y tiene una prueba similar usando la misma idea de considerarla en 3 dimensiones el modelo inicial de 2, describiendo la línea como una intersección de 2 planos.
Véase también
- Centro de homotecia
- Problema de Apolonio, construir un círculo (no necesariamente único) tangente a otros tres círculos dados
Referencias
- Wells, David (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. pp. 153–154. ISBN 0-14-011813-6.
Bibliografía
- Graham, L. A. (1959). Ingenious Mathematical Problems and Methods. New York: Dover. ISBN 0486205452. Consultado el 1 de diciembre de 2012.