Teorema de Routh
En geometría, el teorema de Routh[1] determina la relación de áreas entre un triángulo dado y un triángulo formado por la intersección de tres cevianas (una por cada vértice).
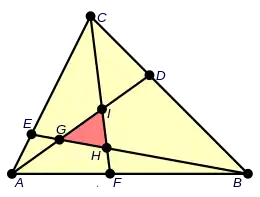
Nomenclatura
Sea un triángulo cualquiera ΔABC (el exterior, amarillo en el gráfico), en cuyos lados AB, BC y CA se han marcado los puntos F, D y E, siendo estos tres últimos pies cualesquiera de las cevianas AD, BE y CF.
Los puntos I, G y H conforman al triángulo interior ΔIGH (color rojo el en el gráfico). Donde I, G y H son los puntos de intersección de las cevianas (AD con CF), (AD con BE) y (BE con CF).
Denominando a las razones de los respectivos segmentos de cada lado como r, s y t:
Llamando a las áreas de los triángulos ΔABC y ΔIGH respectivamente como AABC y AIGH.
Enunciado del teorema
Con la nomenclatura antes mencionada, el teorema de Routh afirma que el área del triángulo ΔIGH es:
El teorema de Ceva puede ser considerado como un caso especial del teorema de Routh. En el caso especial de que las tres cevianas AD, BE y CF se intersequen en un solo punto, entonces el área del triángulo ΔIGH es 0. Se puede concluir que ( r s t = 1 ), lo cual es justamente el enunciado del teorema de Ceva.
Véase también
Enlaces externos
- Routh's Theorem by Cross Products at MathPages
- Routh's Theorem, Jay Warendorff, The Wolfram Demonstrations Project.
Notas y referencias
- El nombre de este teorema es en honor al matemático inglés Edward John Routh FRS (20 de enero de 1831–7 de junio de 1907)
- Murray S. Klamkin and A. Liu, Three more proofs of Routh's theorem, Crux Mathematicorum 7 (1981) 199–203
- H. S. M. Coxeter, Introduction to Geometry, 2nd edition, Wiley, New York, 1969
- J. S. Kline and D. Velleman, Yet another proof of Routh's theorem, Crux Mathematicorum 21 (1995) 37–40
- Weisstein, Eric W. «Routh's Theorem». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.