Teorema de universalidad de Kempe

En 1876, Alfred B. Kempe publicó su artículo On a General Method of describing Plane Curves of the nth degree by Linkwork,[1] que mostró que para una curva plana algebraica arbitraria se puede construir un enlace que dibuje la curva. Esta conexión directa entre los vínculos y las curvas algebraicas se ha denominado teorema de universalidad de Kempe según el cual cualquier subconjunto acotado de una curva algebraica puede trazarse mediante el movimiento de una de las articulaciones en un vínculo adecuadamente elegido. La prueba de Kempe tenía fallas y la primera prueba completa se proporcionó en 2002 basada en sus ideas.[2][3]

Este teorema se ha popularizado describiéndolo como diciendo: "One can design a linkage which will sign your name! [¡Uno puede diseñar un enlace que firmará tu nombre!]"[4]

Kempe reconoció que sus resultados demuestran la existencia de un vínculo de dibujo, pero no sería práctico. Él afirma

Apenas es necesario agregar que este método no sería útil en la práctica debido a la complejidad del trabajo de enlace empleado, una consecuencia necesaria de la perfecta generalidad de la demostración.[1]

Pidiendo al "artista matemático" que encuentre formas más simples de lograr este resultado:

Sin embargo, el método tiene un interés, ya que muestra que hay una manera de dibujar cualquier caso dado; y la variedad de métodos para expresar funciones particulares que ya se han descubierto hace que sea muy probable que en todos los casos se pueda encontrar un método más simple. Todavía hay, sin embargo, un amplio campo abierto para que el artista matemático descubra los enlaces más simples que describan curvas particulares.[1]

Una serie de animaciones que demuestran el trabajo de enlace que resulta del teorema de universalidad de Kempe están disponibles para las curvas de parábola, cúbica autointersecante, cúbica elíptica suave y trifolium.[5]

Vínculos de dibujo más simples

Se han adoptado varios enfoques para simplificar los vínculos de dibujo que resultan del teorema de universalidad de Kempe. Parte de la complejidad surge de los vínculos que Kempe usó para realizar sumas y restas de dos ángulos, la multiplicación de un ángulo por una constante y la traducción de la rotación de un vínculo en una ubicación a la rotación de un segundo vínculo en otra ubicación. Kempe llamó a estos enlaces: enlaces de adición, inversión, multiplicación y traducción, respectivamente. El enlace de dibujo se puede simplificar utilizando diferenciales de engranajes cónicos para sumar y restar ángulos, trenes de engranajes para multiplicar ángulos y transmisiones por correa o cable para traducir ángulos de rotación.[6]

Otra fuente de complejidad es la generalidad de la aplicación de Kempe a todas las curvas algebraicas. Al centrarse en curvas algebraicas parametrizadas, el álgebra de cuaterniones duales se puede utilizar para factorizar el polinomio de movimiento y obtener un vínculo de dibujo.[7] Esto se ha ampliado para proporcionar movimiento del efector final, pero de nuevo para curvas parametrizadas.[8]

La especialización de las curvas en aquellas definidas por polinomios trigonométricos ha proporcionado otra forma de obtener vínculos de dibujo más simples.[9] Las curvas de Bezier se pueden escribir en forma de polinomios trigonométricos, por lo tanto, se puede diseñar un sistema de enlace que dibuje cualquier curva que se aproxime mediante una secuencia de curvas de Bezier.[10]

Visualizaciones

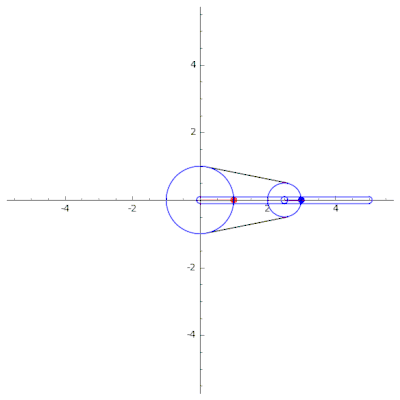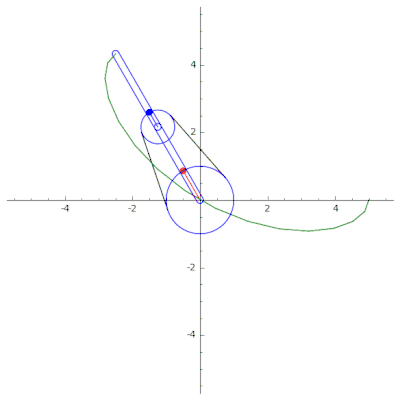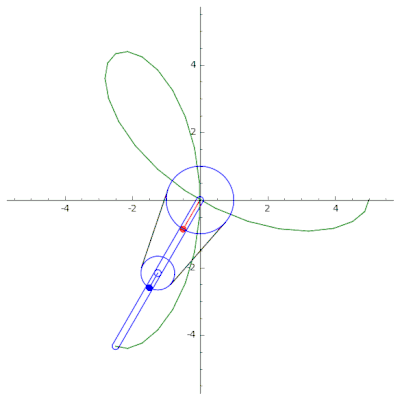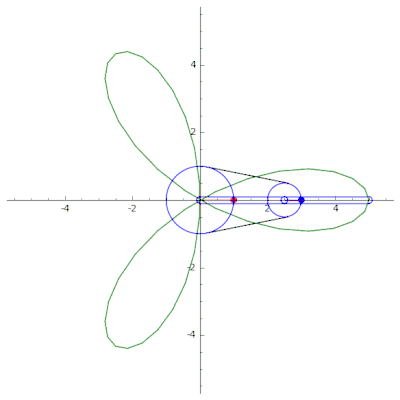
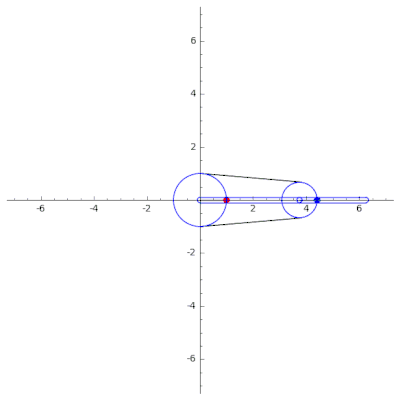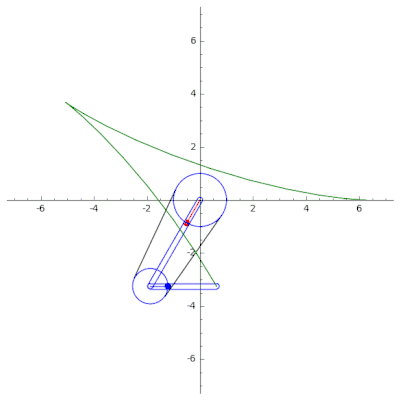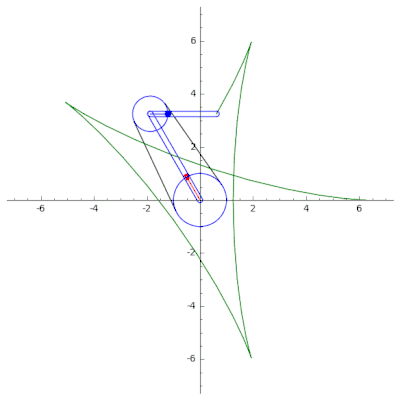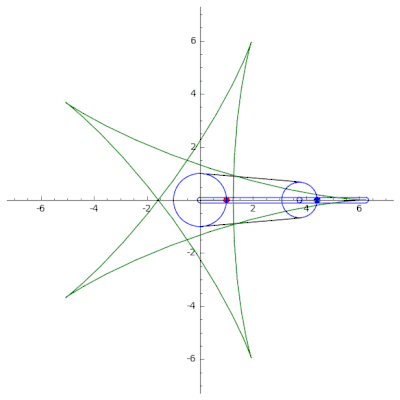
A continuación se muestra un ejemplo de un mecanismo de cadena en serie de un solo acoplamiento, utilizado para dibujar la curva trifolium (izquierda) y la curva hipocicloide (derecha). Usando SageMath. El código fuente se puede encontrar en GitHub .[11]

Véase también

Referencias
  1. Kempe, A. B. (1875). «On a General Method of describing Plane Curves of the nth degree by Linkwork». Proceedings of the London Mathematical Society. s1-7: 213-216. doi:10.1112/plms/s1-7.1.213.
  2. M. Kapovich and J. J. Millson (2002), Universality theorems for configguration spaces of planar linkages Topology, Pergamon Press.
  3. Demaine, Erik; O'Rourke, Joseph (2007), «3.2 Kempe's Universality Theorem», Geometric Folding Algorithms, Cambridge University Press, pp. 31-40, ISBN 978-0-521-71522-5..
  4. J. Malkevich, Feature Column, American Mathematical Society.
  5. A. Kobel, (2008) Automated Generation of Kempe Linkages for Algebraic Curves in a Dynamic Geometry System. Saarland University, Saarbrucken, Germany, Faculty of Natural Sciences and Technology I, Department of Computer Science.
  6. Liu, Yang; McCarthy, J. Michael (2017). «Synthesis of a linkage to draw a plane algebraic curve». Mechanism and Machine Theory 111: 10-20. doi:10.1016/j.mechmachtheory.2016.12.005.
  7. G.Hegedus, Z. Li, J. Schicho, H. P. Schrocker (2015), From the Fundamental Theorem of Algebra to Kempe’s Universality Theorem
  8. M. Gallet, C. Koutschan, Z. Li, G. Regensburger, J. Schicho, and N. Villamiza (2017), Planar Linkages Following a Prescribed Motion, Mathematics of Computation, 86(303), pages 473-506.
  9. Y. Liu and J. M. McCarthy (2017), Design of Mechanisms to Draw Trigonometric Plane Curves, J of Mechanisms and Robotics, 9(2), 024503
  10. Y. Liu and J. M. McCarthy (2017), Design of a Linkage System to Write in Cursive, J of Computers and Information in Science and Engineering, 17(3)
  11. Y. Liu and J. M. McCarthy (2017), Design of Mechanisms to Draw Trigonometric Plane Curves, J of Mechanisms and Robotics, 9(2), 024503

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.