Teselado regular

Según Branko Grünbaum y Shephard (sección 1.2), se dice que un teselado está hecho a la perfección si el grupo de simetría del teselado opera transitivamente sobre los elementos del teselado, donde un elemento consiste de un vértice mutuamente incidente, una arista y una tesela. Esto significa que por cada par de elementos hay una operación de simetría que los asocia entre sí.

Esto es equivalente a un teselado arista con arista de polígonos regulares congruentes. Debe haber seis triángulos, cuatro cuadrados o tres hexágonos regulares en cada vértice, produciendo las tres teselaciones regulares.

36 Teselado triangular

44 Teselado cuadrado

63 Teselado hexagonal

La transitividad de vértice significa que por cada par de vértices existe una operación de simetría que asocia el primer vértice con el segundo.

Si el requisito de la transitividad de elemento se relaja a transitividad de vértice, mientras que se mantiene la condición de la teselación arista con arista, aparecen ocho teselaciones adicionales posibles, conocidas como teselados de Arquímedes, uniformes o teselados semirregulares. Téngase en cuenta que hay dos formas especulares (enantiomorfas o quirales) del teselado 3⁴.6 (hexagonal romo), las cuales se muestran en la siguiente tabla. Todos los otros teselados regulares y semirregulares son aquirales.

34.6 Teselado hexagonal romo	34.6 Teselado hexagonal romo (reflexión)	3.6.3.6 Teselado trihexagonal
33.42 Teselado triangular elongado	32.4.3.4 Teselado cuadrado romo	3.4.6.4 Teselado Rombitrihexagonal
4.82 Teselado cuadrado truncado	3.122 Teselado hexagonal truncado	4.6.12 Teselado trihexagonal truncado

Grünbaum y Shephard distinguen la descripción de estos teselados como de Arquímedes refiriéndose únicamente a la propiedad local de que la disposición de las teselas alrededor de cada vértice es la misma, y el término uniforme se refiere a la propiedad global de la transitividad de vértice. Aunque estos producen el mismo conjunto de teselados en el plano, en otros espacios existen teselados de Arquímedes que no son uniformes.

Los ángulos internos de los polígonos que confluyen en un vértice deben sumar 360 grados. Un ${\displaystyle n\,\!}$-gono regular tiene un ángulo interno de ${\displaystyle (1-{\frac {2}{n}})180}$ grados. Hay diecisiete combinaciones de polígonos regulares cuyos ángulos interiores suman 360 grados, cada uno referido a una especie de vértice, y en cuatro casos hay dos órdenes distintos cíclicos de polígonos, produciendo veintiún tipos de vértice. Solo once de estos pueden presentarse en un teselado uniforme de polígonos regulares. En particular, si hay tres polígonos que se encuentran en un vértice y uno tiene un número impar de lados, los otros dos polígonos deben ser del mismo tamaño. Si no es así, tendrían que alternarse alrededor del primer polígono, lo cual es imposible si su número de lados es impar.

Con tres polígonos en un vértice:

• 7.3.42 (no puede aparecer en ningún teselado de polígonos regulares)
• 8.3.24 (no puede aparecer en ningún teselado de polígonos regulares)
• 9.3.18 (no puede aparecer en ningún teselado de polígonos regulares)
• 3.10.15 (no puede aparecer en ningún teselado de polígonos regulares)
• 3.12² - semi-regular, teselado hexagonal truncado
• 4.5.20 (no puede aparecer en ningún teselado de polígonos regulares)
• 4.6.12 - semi-regular, teselado trihexagonal truncado
• 4.8² - semirregular, teselado cuadrado truncado
• 5².10 (no puede aparecer en ningún teselado de polígonos regulares)
• 6³ - regular, teselado hexagonal

A continuación se presentan los diagramas de vértices como:

• 
  3.7.42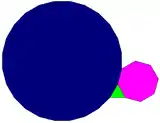
• 
  3.8.24
• 
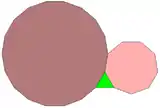  3.9.18
• 
  3.10.15
• 
  3.12.12
• 
  4.5.20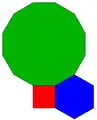
• 
  4.6.12
• 
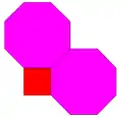  4.8.8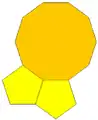
• 
  5.5.10
• 
  6.6.6

Con cuatro polígonos en un vértice:

• 3².4.12 - no uniforme, hay dos tipos de vértices: 3².4.12 y 3⁶
• 3.4.3.12 - no es uniforme, tiene dos tipos diferentes de vértices: 3.4.3.12 y 3.3.4.3.4
• 3².6² - no es uniforme, se presenta en dos modelos con vértices: 3².6²/3⁶ and 3².6²/3.6.3.6.
• 3.6.3.6 - semirregular, teselado trihexagonal
• 4⁴ - regular, teselado cuadrado
• 3.4².6 - no es uniforme, tiene vértices 3.4².6 y 3.6.3.6.
• 3.4.6.4 - semi-regular, teselado rombitrihexagonal

A continuación se presentan los diagramas de vértices como:

• 
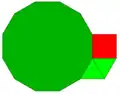  3.3.4.12
• 
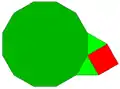  3.4.3.12
• 
  3.3.6.6
• 
  3.6.3.6
• 
  4.4.4.4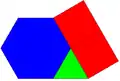
• 
  3.4.4.6
• 
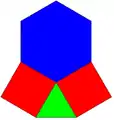  3.4.6.4

Con 5 polígonos en un vértice:

• 3⁴.6 - teselado hexagonal romo, posee dos formas entianomórficas o quirales
• 3³.4² - semirregular, teselado triangular elongado
• 3².4.3.4 - semirregular, teselado cuadrado romo

A continuación se presentan los diagramas de vértices como:

• 
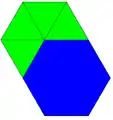  3.3.3.3.6
• 
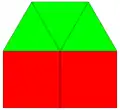  3.3.3.4.4
• 
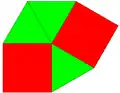  3.3.4.3.4

Con 6 polígonos en un vértice:

• 3⁶ - regular, Teselado triangular

Debajo figura su diagrama:

• 
  3.3.3.3.3.3

Se puede dibujar cualquier número de teselados no-uniformes de polígonos regulares con aristas compartidas (arista con arista). He aquí cuatro ejemplos:

32.62 y 36	32.62 y 3.6.3.6
32.4.12 y 36	3.42.6 y 3.6.3.6

Tales teselados periódicos se pueden clasificar por el número de órbitas de los vértices, aristas y teselas. Si hay ${\displaystyle n}$ órbitas de vértices, el teselado se conoce como ${\displaystyle n}$-uniforme o ${\displaystyle n}$-isogonal; si hay ${\displaystyle n}$ órbitas de teselas, es llamado ${\displaystyle n}$-isoédrico, si hay ${\displaystyle n}$ órbitas de aristas, es llamado ${\displaystyle n}$-isotoxal. Los ejemplos anteriores son cuatro de los veinte teselados 2-uniformes. Chavey clasifica todos los teselados de polígonos regulares con aristas compartidas que son al menos 3-uniformes, 3-isoédricos o 3-isotoxales.

Estos teselados están también relacionados con los poliedros regulares y semirregulares y los teselados del plano hiperbólico. Los poliedros semirregulares se hacen a partir de caras que son polígonos regulares, pero sus ángulos en un punto suman menos de 360 grados. Los polígonos regulares en la geometría hiperbólica tienen ángulos más pequeños que el que poseen en el plano. En ambos casos, que la disposición de polígonos sea la misma en cada vértice, no significa que el poliedro o el teselado sea vértice-transitivo.

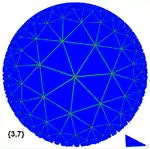
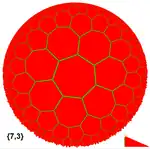
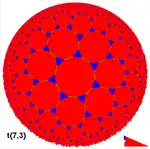
Algunos teselados regulares del plano hiperbólico (usando la proyección del modelo de disco de Poincaré) son:

• Lista de teselados uniformes
• Símbolo de Wythoff
• Teselación
• Grupo cristalográfico plano
• Poliedro regular (Sólidos platónicos)
• Poliedro semirregular (incluyendo a los sólidos de Arquímedes)
• Geometría hiperbólica
• Teselado de Penrose
• Teselado con rectángulos

• Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1.
• D. Chavey (1989). «Tilings by Regular Polygons—II: A Catalog of Tilings». Computers & Mathematics with Applications 17: 147-165. doi:10.1016/0898-1221(89)90156-9.
• D. M. Y. Sommerville, An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes

Enlaces a teselados generales y euclídeos:

• Dutch, Steve. «Uniform Tilings». Archivado desde el original el 9 de septiembre de 2006. Consultado el 9 de septiembre de 2006.
• Mitchell, K. «Semi-Regular Tilings». Consultado el 9 de septiembre de 2006.
• Weisstein, Eric W. «Semiregular tessellation». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
  • Weisstein, Eric W. «Demiregular tessellation». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.

Enlaces a teselados hiperbólicos:

• Eppstein, David. «The Geometry Junkyard: Hyperbolic Tiling». Consultado el 9 de septiembre de 2006.

• Hatch, Don. «Hyperbolic Planar Tessellations». Archivado desde el original el 28 de septiembre de 2006. Consultado el 9 de septiembre de 2006.

• Joyce, David. «Hyperbolic Tessellations». Consultado el 9 de septiembre de 2006.