Vecindad de Moore
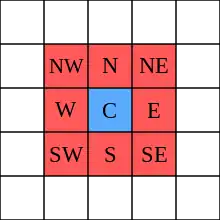
En la teoría de autómatas celulares, la Vecindad de Moore se define como el conjunto de las ocho celdas que rodean una celda central en un enrejado cuadrado bidimensional. Este criterio de vecindad debe su nombre a Edward F. Moore, un pionero de la teoría de autómatas celulares. Es uno de los criterios más utilizados; el otro es el de la vecindad de von Neumann, formada por las 4 celdas que comparten un lado con la celda central. Por ejemplo, en el bien conocido "juego de la vida" de Conway, se utiliza la vecindad de Moore. Es similar a la idea de los 8 píxeles conectados en los gráficos de ordenador.
El concepto puede ser extendido a dimensiones más altas, por ejemplo formando una vecindad cúbica de 26-celdas para un autómata celular en tres dimensiones, como los utilizados en los "juegos de la vida en 3D".
La vecindad de Moore de un punto es el conjunto de los puntos a una distancia de Chebyshov de valor 1 desde el punto dado.
El número de celdas de la vecindad de Moore de un punto dado considerando r unidades de distancia, es:
Así, para distancia r=1, vale 8; para distancia r=2, vale 24; y para r=3 vale 48.[1]
Algoritmo
La idea detrás de la formulación de la vecindad de Moore es encontrar el contorno de un grafo dado. Esta idea era un reto importante para muchos analistas del siglo XVIII. De su trabajo resultó una rutina derivada del grafo de Moore, más tarde denominada como "algoritmo de vecindad de Moore".
A continuación figura una descripción formal del algoritmo que localiza la vecindad de Moore:
Entrada: Una teselación cuadrada, T, conteniendo un conjunto conexo P de celdas negras. Salida: Una secuencia B (b1, b2, ..., bk) de píxeles de frontera, es decir, el contorno. Definir M(a) para ser la vecindad de Moore del píxel a. p denota el píxel de frontera actual. c denota el píxel actualmente considerado, es decir, c pertenece a M(p). b denota el píxel anterior al c (es decir, el píxel vecino al p anteriormente probado)
Empieza
Vaciar B
Recorrer de abajo a arriba y de izquierda a derecha, las celdas de T hasta encontrar un píxel negro s, de P
Insertar s en B
Poner el punto de frontera actual p como s (es decir, p=s)
Hacer b = el píxel desde el que s se introdujo durante el recorrido de la imagen
Seleccionar c para ser el próximo píxel en el sentido de las agujas del reloj (desde b) en M(p)
Mientras c no sea igual a s, hacer:
Si c es negro:
Insertar c en B
Hacer b = p
Hacer p = c
(retroceder: mover el píxel actual c al píxel desde el que p fue introducido)
Hacer c = siguiente píxel en el sentido de las agujas del reloj (desde b) en M(p)
Si no lo es:
(avanzar el píxel actual c al próximo píxel en el sentido de las agujas del reloj en M(p) y actualizar la orden retroceder)
Hacer b = c
Hacer c = siguiente píxel en el sentido de las agujas del reloj (desde b) en M(p)
Fin del Si
Fin del Mientras
Fin
Condición de terminación
La condición de terminación original era parar después de visitar el píxel de inicio por segunda vez. Esto limita el conjunto de contornos que el algoritmo recorrerá completamente. Una condición de parada mejorada propuesta por Jacob Eliosoff consiste en parar tras introducir el píxel de inicio por segunda vez en la misma dirección en la que se introdujo originalmente.
Aplicaciones
Debido a su flexibilidad, es ampliamente utilizado en la mayoría de los editores de imagen como el Adobe Photoshop y el Adobe Fireworks. Se utiliza como motor en las herramientas dedicadas al reconocimiento del contorno de imágenes. Algunas de estas herramientas son el visor de borde y la "varita mágica", diseñados para la administración apropiada y la asignación de las fronteras y los bordes de una imagen digital.
Véase también
Referencias
- Weisstein, Eric W. «Moore Neighborhood». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Tyler, Tim, The Moore neighborhood at cell-auto.com