Vecindad de von Neumann
En la teoría de autómatas celulares, el concepto de vecindad de von Neumann se define como el conjunto de las cuatro celdas que rodean ortogonalmente a una celda central en un enrejado cuadrado bidimensional.[1] Debe su nombre a John von Neumann, quien utilizó este concepto para definir en su interior el autómata celular de von Neumann y el constructor universal de von Neumann.[2] Es uno de los dos criterios de vecindad más utilizados generalmente para autómatas celulares bidimensionales. El otro es el de vecindad de Moore. Es similar a la idea de la conexión de 4 píxeles en los gráficos de ordenador.[3]
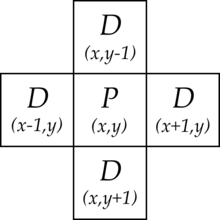
El concepto puede ser extendido a dimensiones más altas, por ejemplo formando una vecindad octaédrica de 6 celdas para un autómata celular cúbico en tres dimensiones.[4]
La vecindad de von Neumann de un punto es el conjunto de puntos situados a una distancia de Manhattan de valor 1 respecto al punto dado.
Vecindad de von Neumann de rango r
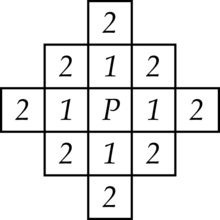
La extensión del concepto de la vecindad de von Neumann sencilla descrita anteriormente, también sirve para determinar el conjunto de puntos a una distancia de Manhattan con r > 1. El resultado es una región en forma de diamante (se muestra para r = 2 en la ilustración). Se denominan vencindades de von Neumann de rango o extensión r. El número de celdas de la vecindad de von Neumann para un espacio d-dimensional y rango r es el correspondiente número de Delannoy D(d,r).[4]
Véase también
Referencias
- Toffoli, Tommaso; Margolus, Norman (1987), Cellular Automata Machines: A New Environment for Modeling, MIT Press, p. 60..
- Ben-Menahem, Ari (2009), Historical Encyclopedia of Natural and Mathematical Sciences, Volume 1, Springer, p. 4632, ISBN 9783540688310..
- Wilson, Joseph N.; Ritter, Gerhard X. (2000), Handbook of Computer Vision Algorithms in Image Algebra (2nd edición), CRC Press, p. 177, ISBN 9781420042382.
- Breukelaar, R.; Bäck, Th. (2005), «Using a Genetic Algorithm to Evolve Behavior in Multi Dimensional Cellular Automata: Emergence of Behavior», Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation (GECCO '05), New York, NY, USA: ACM, pp. 107-114, ISBN 1-59593-010-8, doi:10.1145/1068009.1068024..
Enlaces externos
- Weisstein, Eric W. «von Neumann Neighborhood». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Tyler, Tim, The von Neumann neighborhood at cell-auto.com