Zonágono

En geometría, un zonágono (del término en inglés zonogon; "polígono zonal") es un polígono convexo con simetría central.[1] De manera equivalente, se trata de un polígono convexo cuyos lados se pueden agrupar en pares paralelos con iguales longitudes y orientaciones opuestas (cuando se recorre el polígono en un sentido determinado).

Zonágono octogonal

Teselado irregular con zonágonos hexagonales

Teselado octogonal mediante cuadrados y rombos

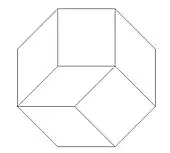
Ejemplos

Un polígono regular es un zonágono si y solo si tiene un número par de lados.[2] Por lo tanto, el cuadrado, el hexágono regular y el octógono regular son todos zonógonos.

Los zonógonos de cuatro lados son el cuadrado, el rectángulo, el rombo y los paralelogramos.

Teselado y equidisección

Los zonágonos de cuatro lados y de seis lados son paralelógonos, capaces de formar mosaicos en el plano mediante copias trasladadas de sí mismos, y todos los paralelógonos convexos poseen esta propiedad.[3]

Cada zonágono con $2n$ lados puede ser teselado por ${\tbinom {n}{2}}$ zonágonos de cuatro lados.[4] Para este recubrimiento, se requiere un tipo de zonágono de cuatro lados por cada par de pendientes distintas de los lados del zonágono de $2n$ lados a recubrir. Al menos tres de los vértices del zonágono deben ser vértices de solo una de las teselas de cuatro lados en cualquiera de tales recubrimientos.[5] Por ejemplo, el octógono regular puede ser recubierto por dos cuadrados y por cuatro rombos con ángulos de 45°.[6]

En una generalización del teorema de Monsky,Paul Monsky (1990) demostró que ningún zonágono posee una equidisección con un número impar de triángulos de igual área.[7][8]

Otras propiedades

En un zonágono de $n$ lados, como máximo $2n-3$ pares de vértices pueden estar a una distancia unidad entre sí. Existen zonágonos con $n$ lados $2n-O({\sqrt {n}})$ pares a distancia unidad.[9]

Formas relacionadas

Los zonágonos son los análogos bidimensionales de los zonaedros tridimensionales y de los zonátopos de mayor dimensión. Como tales, cada zonágono puede ser generado como la suma de Minkowski de una colección de segmentos rectos en el plano.[1] Si no hay dos segmentos paralelos, habrá un par de lados paralelos por cada segmento de línea. Cada cara de un zonahedro es un zonágono, y cada zonágono es la cara de al menos un zonaedro, el prisma sobre ese zonágono. Además, cada sección transversal plana a través del centro de un poliedro centralmente simétrico (como un zonaedro) es un zonágono.

Referencias

Boltyanski, Vladimir; Martini, Horst; Soltan, P. S. (2012), Excursions into Combinatorial Geometry, Springer, p. 319, ISBN 9783642592379.
Young, John Wesley; Schwartz, Albert John (1915), Plane Geometry, H. Holt, p. 121, «If a regular polygon has an even number of sides, its center is a center of symmetry of the polygon ».
Alexandrov, A. D. (2005), Convex Polyhedra, Springer, p. 351, ISBN 9783540231585.
Beck, József (2014), Probabilistic Diophantine Approximation: Randomness in Lattice Point Counting, Springer, p. 28, ISBN 9783319107417.
Andreescu, Titu; Feng, Zuming (2000), Mathematical Olympiads 1998-1999: Problems and Solutions from Around the World, Cambridge University Press, p. 125, ISBN 9780883858035.
Frederickson, Greg N. (1997), Dissections: Plane and Fancy, Cambridge University Press, Cambridge, p. 10, ISBN 0-521-57197-9, MR 1735254, doi:10.1017/CBO9780511574917.
Monsky, Paul (1990), «A conjecture of Stein on plane dissections», Mathematische Zeitschrift 205 (4): 583-592, MR 1082876, doi:10.1007/BF02571264.
Stein, Sherman; Szabó, Sandor (1994), Algebra and Tiling: Homomorphisms in the Service of Geometry, Carus Mathematical Monographs 25, Cambridge University Press, p. 130, ISBN 9780883850282.
Ábrego, Bernardo M.; Fernández-Merchant, Silvia (2002), «The unit distance problem for centrally symmetric convex polygons», Discrete and Computational Geometry 28 (4): 467-473, MR 1949894, doi:10.1007/s00454-002-2882-5.

Datos: Q47008488

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[bms-1] Boltyanski, Vladimir; Martini, Horst; Soltan, P. S. (2012), Excursions into Combinatorial Geometry, Springer, p. 319, ISBN 9783642592379.

[ys-2] Young, John Wesley; Schwartz, Albert John (1915), Plane Geometry, H. Holt, p. 121, «If a regular polygon has an even number of sides, its center is a center of symmetry of the polygon ».

[aa-3] Alexandrov, A. D. (2005), Convex Polyhedra, Springer, p. 351, ISBN 9783540231585.

[beck-4] Beck, József (2014), Probabilistic Diophantine Approximation: Randomness in Lattice Point Counting, Springer, p. 28, ISBN 9783319107417.

[mo-5] Andreescu, Titu; Feng, Zuming (2000), Mathematical Olympiads 1998-1999: Problems and Solutions from Around the World, Cambridge University Press, p. 125, ISBN 9780883858035.

[gnf-6] Frederickson, Greg N. (1997), Dissections: Plane and Fancy, Cambridge University Press, Cambridge, p. 10, ISBN 0-521-57197-9, MR 1735254, doi:10.1017/CBO9780511574917.

[monsky-7] Monsky, Paul (1990), «A conjecture of Stein on plane dissections», Mathematische Zeitschrift 205 (4): 583-592, MR 1082876, doi:10.1007/BF02571264.

[ss-8] Stein, Sherman; Szabó, Sandor (1994), Algebra and Tiling: Homomorphisms in the Service of Geometry, Carus Mathematical Monographs 25, Cambridge University Press, p. 130, ISBN 9780883850282.

[af-9] Ábrego, Bernardo M.; Fernández-Merchant, Silvia (2002), «The unit distance problem for centrally symmetric convex polygons», Discrete and Computational Geometry 28 (4): 467-473, MR 1949894, doi:10.1007/s00454-002-2882-5.