Équation d'état pvT
L'équation d'état pvT est la relation qui lie, pour un système :
- la pression, exprimée en pascals (Pa) ;
- le volume spécifique v = 1/ρ, exprimé en mètres cubes par kilogramme (m3·kg−1) ;
- la température thermodynamique T, exprimée en kelvins (K).
Pour les articles homonymes, voir Diagramme pvT.
Elle est utilisée pour représenter la compressibilité des polymères, notamment dans les problèmes d'injection plastique.
On trace typiquement un faisceau de courbes v = ƒ(T) pour plusieurs pressions. La gamme de température va typiquement de la température ambiante 20 °C à la température maximale du procédé, de l'ordre de 300 °C, et pour les pressions allant de l'ambiante (1 bar à la pression d'injection considérée (jusqu'à quelques centaines de bars).
De manière générale, pour une pression donnée, v augmente avec T (dilatation). Et pour une température donnée, v diminue avec p (compression).
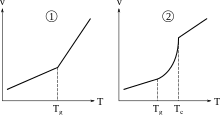
On a typiquement deux types de comportements :
- pour un polymère amorphe, le diagramme (v, T)p commence par une droite de faible pente, puis au-delà de la température de transition vitreuse, on a une droite de pente plus forte : le polymère pâteux/liquide se dilate plus que le polymère solide ;
- pour un polymère semi-cristallin, on a une courbe « en S » en raison de la fusion des cristaux au chauffage, ou de la cristallisation au refroidissement : à l'état cristallisé, les chaînes sont alignées et donc prennent « peu de place », on a donc un « saut » au réchauffement au moment où les chaînes se « libèrent ».

Le comportement d'un polymère semi-cristallin dépend de son taux de cristallinité, et donc de la vitesse de refroidissement. De manière générale, on a un effet d'hystérésis entre le chauffage et le refroidissement, similaire à la surfusion. On constate également qu'à l'état solide, le comportement dépend de la vitesse de chauffage ou refroidissement : une vitesse de refroidissement rapide (trempe) génère des contraintes internes qui modifient le comportement du matériau.
Établissement du diagramme pvT
Le diagramme pvT est établi expérimentalement. Il existe plusieurs techniques dilatométriques[1].
La première technique est celle du piston-matrice : le polymère est mis dans un cylindre (matrice) et comprimé par un piston. Le piston applique une pression constante p, et l'on mesure le déplacement Δl du piston. Cette méthode est simple à mettre en œuvre, mais :
- la pression n'est pas parfaitement hydrostatique, car le matériau « colle » aux parois ;
- il faut maîtriser les fuites aux fortes pressions.
La deuxième technique est celle du confinement fluide : le matériau est noyé dans un fluide, en général du mercure ou une huile de silicone, le tout étant placé dans une enceinte étanche à parois rigides, à l'exception d'une qui est souple ou bien en soufflet et sert à exercer la pression (équivalent du piston). La pression est hydrostatique, mais :
- la méthode est plus complexe à mettre en œuvre ;
- il faut corriger des variations de volume du fluide de confinement ;
- il peut y avoir des réactions entre le fluide de confinement et le polymère.
Certains cherchent à développer des mesures « en production » (in-line), c'est-à-dire en utilisant directement les vis d'extrusion ou les machines d'injection, ce qui permettrait de mieux maîtriser les procédés de fabrication. On peut par exemple utiliser la position du piston ou de la vis d'injection pour avoir accès au volume, et mettre des capteurs de température dans le moule.
Modèles
Modèle de Tait à double domaine

Le modèle de Tait à double domaine est une équation semi-empirique v = ƒ(p, T), dépendant d'une constante C dite « universelle », et de treize paramètres dépendant du polymère bi, qui sont ajustés à partir de données expérimentales. On distingue deux domaines séparés par une température de transition Tt dépendant de la pression p, on a donc des paramètres définis au-delà de Tt, portant l'indice m (molten, fondu), et des paramètres définis en deçà de Tt, portant l'indice s (solide).
avec :
- T > Tt :
- v0 = b1m + b2m·T*,
- B = b3m·exp(-b4m·T*),
- vt = 0 ;
- T < Tt :
- v0 = b1s + b2s·T*,
- B = b3s·exp(-b4s·T*),
- vt = b7·exp(b8·T* - b9·p) ;
- Tt = b5 + b6·p ;
- T* = T - b5 ;
- C = 0,0894.
On a :
- b1m, b1s et b7 en m3·kg−1 ;
- b2m et b2s en m3·kg−1·K−1 ;
- b3m et b3s en Pa ;
- b4m et b4s en K−1 ;
- b5 en K ;
- b6 en K·Pa−1 ;
- b8 en K−1 ;
- b9 en Pa−1 ;
- C sans dimension.
Notons que b1m est l'ordonnée à l'origine de la portion de loi (le volume spécifique à pression nulle) de la phase fondue, et b1s + b7 celle de la phase solide. La fonction intermédiaire B(T) est la sensibilité de v à la pression ; v0(T) est la courbe à pression nulle pour la phase fondue.
Dans le cas d'un polymère semi-cristallin, la température de transition Tt correspond à la température de fusion des cristallites, notée Tc ou Tf. Par ailleurs, on a b1m > b1s[2].
Dans le cas d'un polymère entièrement amorphe, la température de transition Tt est la température de transition vitreuse, notée Tv ou Tg, et b1m = b1s[2].
Lorsque la pression est nulle (p = 0), l'écriture se simplifie :
- v = v0 + vt
- Tt = b5
soit :
- T < b5 :
v = b1s + b2s·T* + b7·exp(b8·T*) ; - T > b5 :
v = b1m + b2m·T* ; - T = b5 :
v = b1s + b7 à gauche, v = b1m à droite
Notes et références
- (en) Jian Wang, PVT Properties of Polymers for Injection Molding, Intech, , 284 p. (ISBN 978-953-51-0297-7, lire en ligne), p. 5-15
- (en) Patcharee Larpsuriyakul, Design, analysis and simulation in injection in-mold labelling : thèse de doctorat, Stuttgart, Fakultät Energie-, Verfahrens-, und Biotechnik der Universität Stuttgart, , 160 p. (lire en ligne), p. 43
Articles connexes
- Équation d'état de Murnaghan, utilisée pour les roches en sciences de la Terre
- Portail de la physique
- Portail de la chimie