Température thermodynamique

La température thermodynamique est une formalisation de la notion expérimentale de température et constitue l’une des grandeurs principales de la thermodynamique. Elle est intrinsèquement liée à l'entropie.

Température

Données clés
Unités SI	kelvin (K)
Dimension	Θ
Nature	Grandeur scalaire intensive
Symbole usuel	$T$
Lien à d'autres grandeurs	$\mathrm {d} S={\frac {\delta Q}{T}}$ [alpha 1] $T=\left({\frac {\partial U}{\partial S}}\right)_{V}$ [alpha 2] $T=(k\beta )^{-1}$

Usuellement notée $T$ , la température thermodynamique se mesure en kelvins (symbole K). Encore souvent qualifiée de « température absolue », elle constitue une mesure absolue parce qu’elle traduit directement le phénomène physique fondamental qui la sous-tend : l’agitation des particules constituant la matière (translation, vibration, rotation, niveaux d'énergie électronique). Son point origine, ou zéro absolu, correspond par définition à l’état de la matière où ces particules ont une entropie minimale, ce qui correspond généralement à une énergie minimale[1].

Concept historique de température

La température est une notion qui a évolué avec la connaissance de la matière. On peut distinguer diverses étapes du concept.

Thermodynamique des milieux à l'équilibre

On s'intéresse ici aux états thermodynamiques d'équilibre et aux possibilités (ou à l'impossibilité) de passer de l'un à l'autre par une transformation quasi-statique, c'est-à-dire s'effectuant par une suite d'états d'équilibre. Cette partie de la thermodynamique devrait en toute logique s'appeler « thermostatique », mais ce mot est défini comme adjectif dans un autre sens.

Au XVII^e – XVIII^e siècle, l'apparition du thermomètre permet de quantifier les notions d'état chaud ou froid d'un milieu, quantités accessibles à la perception corporelle. La température thermométrique est ce que mesure l'appareil : un effet, en l'occurrence la dilatation thermique d'un liquide. Le lien avec la température se fait par le choix d'une échelle de référence, qui est le problème de la thermométrie. Mais cela ne renseigne en rien sur la nature de la température et ne donne que peu d'indications sur ses propriétés.

À la même époque, Joseph Black établit le lien entre température $T$ et chaleur $Q$ en introduisant la capacité thermique $C_{V}$ [2]. Si on se place à volume constant :

\delta Q=C_{V}\,\mathrm {d} T

Cette loi montre que la température est une quantité substituable à la chaleur et donc à l'énergie interne en l'absence de travail.

Les travaux sur les machines thermiques au XIX^e siècle, en particulier ceux de Carnot, montrent l'impossibilité des cycles monothermes. Le deuxième principe de la thermodynamique établi par Rudolf Clausius[3]^,[4] conduit à l'introduction de la notion d'entropie S, liée à une variation de chaleur $\delta Q$ reçue par le système et à la température thermodynamique $T$ . Pour une transformation réversible :

\mathrm {d} S={\frac {\delta Q}{T}}

Cette définition permet d'annuler les échanges de chaleur entre deux milieux de température égale mais ne suffit pas pour définir une température thermodynamique de manière unique.

Cas d'un gaz parfait à volume constant.

Il suffit de deux paramètres pour définir l'état thermodynamique d'un gaz parfait, par exemple l'énergie interne $U$ et le volume $V$ :

S=S\!\left(U,V\right)

Schéma d'un système fermé formé de deux sous-systèmes A et B, séparés par une paroi diatherme.

Considérons l'interaction entre deux systèmes isolés de l'extérieur, séparés par une paroi diatherme qui ne laisse passer aucune particule mais permet les échanges de chaleur (voir figure). Si, initialement, les deux systèmes ne sont pas à l'équilibre, un échange thermique a lieu entre A et B jusqu'à ce que l'équilibre soit atteint. Les volumes de A et B restant invariants, la variation de l'entropie totale, somme des variations des entropies de A et B, ne dépend que des variations d'énergies internes de A et B :

\mathrm {d} S=\left({\frac {\partial S_{\rm {A}}}{\partial U_{\rm {A}}}}\right)_{V_{\rm {A}}}\mathrm {d} U_{\rm {A}}+\left({\frac {\partial S_{\rm {B}}}{\partial U_{\rm {B}}}}\right)_{V_{\rm {B}}}\mathrm {d} U_{\rm {B}}

Puisque le système est isolé, la variation de l'énergie interne totale est nulle ; il en résulte que :

\mathrm {d} U_{\rm {A}}=-\mathrm {d} U_{\rm {B}}

d'où :

\mathrm {d} S=\left[\left({\frac {\partial S_{\rm {A}}}{\partial U_{\rm {A}}}}\right)-\left({\frac {\partial S_{\rm {B}}}{\partial U_{\rm {B}}}}\right)\right]\mathrm {d} U_{\rm {A}}

De plus, comme le système est à l'équilibre, son entropie est maximale : toutes les dérivées partielles de l'entropie sont nulles et :

\left({\frac {\partial S_{\rm {A}}}{\partial U_{\rm {A}}}}\right)_{V_{\rm {A}}}=\left({\frac {\partial S_{\rm {B}}}{\partial U_{\rm {B}}}}\right)_{V_{\rm {B}}}

En l'absence de travail du système considéré on peut écrire :

\delta Q=\mathrm {d} U=T\,\mathrm {d} S

donc :

\left({\frac {\partial U}{\partial S}}\right)_{V}=T

et par suite $T_{\rm {A}}=T_{\rm {B}}$

Ce résultat pourrait être obtenu pour toute fonction monotone $f(T)$ telle que :

\left({\frac {\partial U}{\partial S}}\right)_{V}=f(T)

Le choix $f(T)=T$ correspond au choix d'une échelle de température qui est à justifier.

Divers travaux, en particulier ceux dus à Carathéodory[5]^,[6], permettent de trouver l'expression liant la température à l'entropie à partir de critères mathématiques. En effet on souhaite faire de $\mathrm {d} S$ une différentielle exacte afin que la variation de l'entropie d'un état à un autre soit indépendante du chemin suivi, ce qui n'est pas le cas de $\delta Q$ . La quantité qui apparaît naturellement est $1/T$ , quantité que l'on retrouve comme potentiel dans les échanges hors équilibre (voir ci-dessous). La dernière étape consiste alors à définir une échelle de température. On se base pour cela sur les propriétés d'un gaz parfait[alpha 3], ce qui assure la cohérence de l'approche.

Température et entropie.

Recherche d'un facteur intégrant

On cherche une quantité (facteur intégrant) $w$ , fonction des variables d'état, qui permet de passer de la quantité élémentaire de chaleur $\delta Q$ à une différentielle exacte $\mathrm {d} S$ , $S$ étant alors défini comme entropie du système et sur laquelle on pourra appuyer un raisonnement comme celui de l'encadré précédent[alpha 4] :

w(U,V,p)\cdot \delta Q=\mathrm {d} S

On a :

\mathrm {d} S=w\,\mathrm {d} U+w\,p\,\mathrm {d} V

Le critère utilisé est le théorème de Schwarz :

{\frac {\partial ^{2}S}{\partial U\partial V}}={\frac {\partial ^{2}S}{\partial V\partial U}}

Ici :

{\frac {\partial ^{2}S}{\partial U\partial V}}={\frac {\partial }{\partial U}}\left({\frac {\partial S}{\partial V}}\right)_{U}={\frac {\partial }{\partial U}}\left(w\,p\right)=w\,\left({\frac {\partial p}{\partial U}}\right)_{V}+p\,\left({\frac {\partial w}{\partial U}}\right)_{V}

{\frac {\partial ^{2}S}{\partial V\partial U}}={\frac {\partial }{\partial V}}\left({\frac {\partial S}{\partial U}}\right)_{V}=\left({\frac {\partial w}{\partial V}}\right)_{U}

Parmi tous les facteurs intégrants possibles, on choisit une quantité $T(U,V,p)$ que l'on définit comme température :

\left({\frac {\partial w}{\partial U}}\right)_{V}={\frac {\mathrm {d} w}{\mathrm {d} T}}\left({\frac {\partial T}{\partial U}}\right)_{V}={\frac {1}{C_{V}}}{\frac {\mathrm {d} w}{\mathrm {d} T}}

\left({\frac {\partial w}{\partial V}}\right)_{U}={\frac {\mathrm {d} w}{\mathrm {d} T}}\left({\frac {\partial T}{\partial V}}\right)_{U}=\mu {\frac {\mathrm {d} w}{\mathrm {d} T}}

On a défini les quantités :

$C_{V}$ capacité thermique isochore ;
$\mu$ coefficient de Joule-Gay-Lussac (ou coefficient de Joule-Thomson isoénergétique).

$w$ est donc solution de l'équation :

{\frac {\mathrm {d} w}{w}}=\mathrm {d} \ln w={\frac {\left({\frac {\partial p}{\partial U}}\right)_{V}}{\mu -{\frac {p}{C_{V}}}}}\,\mathrm {d} T={\frac {\left({\frac {\partial p}{\partial T}}\right)_{V}}{\mu C_{V}-p}}\,\mathrm {d} T={\frac {1}{\lambda }}\left({\frac {\partial p}{\partial T}}\right)_{V}\,\mathrm {d} T

Unicité

On remarque que cette équation définit la température à une constante multiplicative près, en effet si l'on pose :

w(T)=\kappa w(\theta )

$\kappa$ ne change pas puisque :

C_{V}(\theta )\,\mu (\theta )=C_{V}(T)\,\mu (T)

et :

{\frac {\mathrm {d} \ln w(\theta )}{\mathrm {d} \theta }}={\frac {\mathrm {d} \ln w(T)}{\mathrm {d} T}}{\frac {\mathrm {d} T}{\mathrm {d} \theta }}={\frac {1}{\lambda }}\left({\frac {\partial p}{\partial T}}\right)_{V}{\frac {\mathrm {d} T}{\mathrm {d} \theta }}={\frac {1}{\lambda }}\left({\frac {\partial p}{\partial \theta }}\right)_{V}

ce qui conduit à une équation identique pour $w(\theta )$ .

Échelle

On a donc montré qu'il existe une variable d'état $T$ telle que ${\frac {\delta Q}{T}}$ soit une différentielle exacte. Il reste à la préciser en choisissant une échelle de référence, laquelle est implicitement liée à une équation d'état. Pour des raisons évidentes on va prendre $\mu =0$ . L'équation sur $w$ se simplifie en :

\mathrm {d} \ln w=-{\frac {1}{p}}\left({\frac {\partial p}{\partial T}}\right)_{V}\,\mathrm {d} T

Prenons le cas d'une transformation isochore d'un état 1 vers un état 2, l'expression de $w$ devient :

\int _{1}^{2}\mathrm {d} \ln \left({\frac {1}{T}}\right)=-\ln {\frac {T_{2}}{T_{1}}}=-\int _{1}^{2}{\frac {1}{p}}\left({\frac {\partial p}{\partial T}}\right)_{V}\mathrm {d} T=-\ln {\frac {p_{2}}{p_{1}}}

On reconnait la loi de Gay-Lussac pour un gaz parfait :

{\frac {T_{2}}{T_{1}}}={\frac {p_{2}}{p_{1}}}

L'équation d'état du gaz parfait est assez naturellement le meilleur choix pour l'échelle de référence[7].

On note que, $S$ et $Q$ étant des quantités extensives, la relation non linéaire les liant fait de $T$ une quantité intensive.

Dans les années 1870, Ludwig Boltzmann énonce le théorème H et l'équation de Boltzmann pour le développement temporel des fonctions de distribution microscopiques[8]. Ces relations fondamentales permettent le lien entre les descriptions microscopique et macroscopique de la physique. L'entropie représente le nombre de configurations microscopiques possibles pour un système donné et la température le paramètre qui, avec le nombre de particules par unité de volume, caractérise entièrement ce système à l'équilibre thermodynamique au travers de la fonction de distribution de Maxwell pour la translation et celle de Boltzmann pour les autres degrés de liberté.

Si on considère la translation, la température est définie à partir de la vitesse quadratique moyenne des particules au niveau microscopique par l'expression suivante issue de la théorie cinétique des gaz :

{\frac {3}{2}}kT={\frac {1}{2}}m{\overline {v^{2}}}

Si on considère les populations $n_{i}$ d'états microscopiques d'énergie $E_{i}$ , la température est donnée par :

kT=-{\frac {E_{j}-E_{i}}{\ln \left({\frac {n_{j}}{n_{i}}}\right)}}

,

\forall i,j

Ces deux valeurs sont identiques en vertu du théorème d'équipartition de l'énergie.

La température au niveau microscopique.

En physique statistique, la fonction de partition d'un système formé d'un ensemble de $N$ états microscopiques d'énergie $E_{i}$ , chacun étant occupé $n_{i}$ fois, est donnée à une constante de normalisation près par :

\Omega ={\frac {N!}{\Pi _{i}n_{i}!}}\,,\;\;\;\;\;N=\sum _{i}n_{i}

L'énergie interne de ce système est :

U={\frac {E}{N}}=\sum _{i}{\frac {n_{i}}{N}}E_{i}

On suppose que le nombre N est suffisamment grand pour que l'on puisse considérer Ω(n) comme une fonction et utiliser l'approximation de Stirling. On a donc :

{\begin{array}{lcl}\log \Omega &=&\log N!-\sum _{i}\log n_{i}!\\[0.6em]&\approx &N\log N-\sum _{i}n_{i}\log n_{i}\end{array}}

L'état d'équilibre est donné par $\Omega ={\text{constante}}$ , soit :

{\frac {\mathrm {d} \log \Omega }{\mathrm {d} n_{i}}}=-\sum _{i}\left(1+\log {\frac {n_{i}}{N}}\right)=0

Ce problème est traité comme un problème d'extremum de $\log \Omega$ avec les contraintes de conservation du nombre de particules $\mathrm {d} N=\sum _{i}\mathrm {d} n_{i}=0$ et de l'énergie $\mathrm {d} E=\sum _{i}E_{i}\,\mathrm {d} n_{i}=0$ . En utilisant deux multiplicateurs de Lagrange $\alpha$ et $\beta$ pour les contraintes sur $N$ et $E$ , respectivement, il vient :

\sum _{i}\left(\log n_{i}+\alpha +\beta E_{i}\right)=0

Les états étant indépendants, cette équation n'est vérifiée que si elle est vraie pour chaque état. Sa solution est donc :

n_{i}=e^{-\alpha }e^{-\beta E_{i}}

L'énergie vaut :

U={\frac {\sum _{i}E_{i}e^{-\beta E_{i}}}{\sum _{i}e^{-\beta E_{i}}}}

En différentiant, on fait apparaître la redistribution d'une énergie donnée sur les divers niveaux d'occupation (chaleur) et la variation d'énergie liée à la variation de volume (travail) :

\mathrm {d} U=\underbrace {\sum _{i}E_{i}\mathrm {d} \left({\frac {n_{i}}{N}}\right)} _{\delta Q}+\underbrace {\sum _{i}{\frac {n_{i}}{N}}\mathrm {d} E_{i}} _{-\delta W}

On définit l'entropie canonique par :

S(E_{i},\beta )=k(\ln \Omega +\beta U)+S_{0}

On peut définir une différentielle exacte :

\mathrm {d} S=\sum _{i}\left({\frac {\partial S}{\partial E_{i}}}\right)_{\beta }\mathrm {d} E_{i}+\left({\frac {\partial S}{\partial \beta }}\right)_{E_{i}}\mathrm {d} \beta =k\beta \delta Q

D'où la valeur de $\beta$ par identification avec l'expression classique de la thermodynamique $\mathrm {d} S={\frac {\delta Q}{T}}$ :

k\beta ={\frac {1}{T}}

Le raisonnement s'applique de la même manière pour le système continu que constitue la translation des particules, les quantités discrètes étant remplacées par les distributions d'énergie et de populations de particules de masse $m$ et de vitesse $v$ [7] :

E_{i}={\frac {1}{2}}\,m\,{v_{i}}^{2}

et, d'après la loi de distribution des vitesses de Maxwell :

\mathrm {d} \left({\frac {n_{i}}{N}}\right)={\frac {2}{\sqrt {\pi }}}\,\beta ^{\frac {3}{2}}\,{E_{i}}^{\frac {1}{2}}\,e^{-\beta E_{i}}\,\mathrm {d} E_{i}

Thermodynamique hors équilibre

On parle ici de thermodynamique hors équilibre, c'est-à-dire des chemins permettant de passer d'un état d'équilibre à un autre par des processus de transport ou de relaxation dans un milieu proche de l'équilibre thermodynamique, cette dernière condition étant nécessaire pour exprimer les flux sous forme de lois linéaires.

Au XVIII^e siècle, Joseph Fourier établit la loi portant son nom qui semble faire de la température le potentiel scalaire permettant de connaitre le flux de chaleur[9] :

\mathbf {q} =-\lambda \,\nabla T

En fait, la thermodynamique hors équilibre montre que cette expression devrait être écrite :

\mathbf {q} =\lambda '\,\nabla \left({\frac {1}{T}}\right)

$1/T$ est l'affinité, qui constitue le potentiel lié à l'énergie $U$ . $1/T$ apparaît également dans les phénomènes de diffusion de la matière par l'intermédiaire du gradient $\nabla \left({\frac {\mu }{T}}\right)$ où $\mu$ est le potentiel chimique.

Remarques sur la notion de température

Zéro absolu

Le zéro absolu, qui correspondrait à une matière totalement figée, est interdit par le principe d'incertitude de la mécanique quantique, qui prohibe tout état où l'on connaitrait simultanément position et vitesse. La description continue du degré de liberté en translation n'est donc pas pertinente pour les très basses températures. On ne peut pas, pour compter les états, prendre de boîte de taille inférieure à la longueur de Planck.

La température étant indissociablement liée à l'entropie, c'est cette valeur qui va guider une définition du zéro absolu comme température associée à l'entropie minimale :

\lim \limits _{T\to 0}S=k\ln g_{0}

où $g_{0}$ est la dégénérescence du niveau d'énergie le plus bas. Si on peut considérer que, en théorie, $g_{0}=1$ , il n'en va pas de même en pratique où de faibles perturbations du système mesuré vont lever la dégénérescence et empêcher l'obtention du zéro absolu. La valeur la plus basse de 450 pK a été atteinte dans un gaz de sodium au Massachusetts Institute of Technology par l'équipe de Wolfgang Ketterle[10].

Troisième principe de la thermodynamique

L'entropie microscopique d'un système est donnée par :

S=k\ln \Omega +{\frac {U}{T}}+S_{0}

où $\Omega$ est la fonction de partition et $S_{0}$ une constante d'intégration arbitraire que l'on prendra égale à zéro[11].

On a (voir encadré précédent) :

U=-{\frac {\partial \ln \Omega }{\partial \beta }}=kT\,{\frac {\partial \ln \Omega }{\partial \ln T}}

\Omega =\sum _{i}{\frac {n_{i}}{N}}e^{-{\frac {E_{i}}{kT}}}

D'où la limite correspondant à l'énergie minimale :

\lim \limits _{T\to 0}S=k\ln g_{0}

où $g_{0}$ est la dégénérescence du niveau fondamental.

Échelle absolue de température

Le deuxième principe de la thermodynamique a permis de définir la température et une échelle de référence pour celle-ci, basée sur l'équation d'état du gaz parfait (voir encadré « Température et entropie »). L'instrument primaire de mesure est donc assez naturellement un thermomètre à hydrogène, gaz dont le comportement est proche de celui du gaz parfait et qui est peu sensible au phénomène d'adsorption pariétale comme le sont les gaz nobles. Comme on sait définir le zéro absolu, il reste à définir un point de référence. La norme actuelle choisit d'utiliser le point triple d'une eau de composition isotopique donnée comme constituant par définition la valeur 273,16 K[12].

Température de rayonnement

Source de rayonnement gazeux.

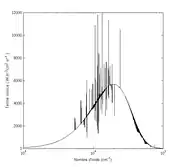
Le rayonnement électromagnétique est constitué de photons qui se comportent au plan thermodynamique comme un gaz. Les échanges matière-rayonnement peuvent permettent à ce dernier d'acquérir un équilibre thermodynamique caractérisé par la distribution de Planck à la température $T$ du milieu matériel, qui constitue la température du rayonnement. En l'absence d'interaction photon-photon (en) pour assurer des échanges d'énergie, il faut multiplier les interactions photon-matière pour aboutir à l'équilibre thermodynamique. Un tel rayonnement est appelé rayonnement du corps noir. Il est obtenu par l'utilisation d'une enceinte fermée. Le rayonnement que l'on rencontre dans de nombreux domaines s'éloigne de celui-ci en comportant des raies d'émission ou d'absorption.

L'équilibre thermodynamique du rayonnement correspond à une distribution angulaire de celui-ci isotrope. À l'opposé, un rayon lumineux de fréquence $\nu$ correspond à une entropie minimale[13] :

S={\frac {4\pi \ln 2\,k\nu ^{2}}{c^{3}}}

Celle-ci tend vers zéro lorsque la longueur d'onde augmente.

Pour un spectre de rayonnement différent de celui du corps noir on définit une température $\textstyle T_{R}$ par analogie avec la température du corps noir par $\textstyle E_{R}=aT_{R}^{4}$ où $\textstyle a$ est la constante radiative. Si l'énergie radiative $\textstyle E_{R}$ est une quantité physique parfaitement définie, la température radiative ainsi définie n'a pas de grande signification mais elle permet de se ramener à une notion habituelle.

Milieu à plusieurs températures

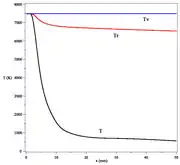
Températures de vibration T_v, de translation T et de rotation T_r dans une détente d'azote.

L'équilibre thermodynamique entraîne l'existence d'une température unique pour tous les degrés de liberté du milieu : translation, décrite par la statistique de Maxwell, rotation, vibration et énergie interne, décrites par la statistique de Boltzmann. Dans certaines situations créés par l'introduction d'énergie dans le système, il se crée des états proches de l'équilibre qui peuvent être raisonnablement bien décrits par plusieurs températures. C'est par exemple le cas d'un plasma froid qui présente des températures de translation différentes pour les électrons et les particules lourdes : ions, atomes, molécules. On peut séparer localement les divers degrés de liberté en effectuant une forte détente (voir figure) à partir des temps caractéristiques différents pour les divers couplages entre ceux-ci[14]. Un tel système relaxe rapidement vers l'équilibre thermodynamique.

Milieu dans lequel la température n'est pas un paramètre pertinent

Effet Sunyaev-Zel'dovich : le spectre de corps noir

L_{CN}

est modifié par comptonisation.

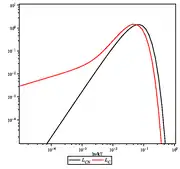
Dans le cas où l'énergie injectée dans le milieu est très importante, la distribution microscopique s'éloigne notablement des distributions d'équilibre. Il peut cependant se créer des états stationnaires comme dans l'effet Sunyaev-Zel'dovich issu d'interactions Compton multiples (comptonisation). Ce milieu possède une entropie et une énergie interne pour chaque constituant, électrons et photons. On peut donc lui associer deux températures, mais celles-ci n'ont que peu d'intérêt car elle ne permettent pas de caractériser les distributions d'énergie correspondantes.

Température négative

Certains systèmes quantiques liés à la résonance magnétique nucléaire dans les cristaux ou les gaz ultrafroids possèdent des distributions d'énergie particulière pouvant être entièrement peuplées dans l'état de plus basse énergie (zéro absolu) mais également dans l'état de plus haute énergie[15]. Dans les deux cas, l'entropie est nulle par définition. Entre les deux extrêmes, l'entropie est finie, ce qui fait que $S$ est une fonction de $U$ d'abord croissante, puis décroissante. Si on adopte la définition standard de la température, cela conduit à une valeur infinie au maximum d'entropie, suivie de valeurs négatives pour les hautes énergies[16]. Ce problème est lié à la définition de l'entropie de Boltzmann, mais il disparaît si l'on utilise une définition alternative donnée par Willard Gibbs[17].

Ce problème illustre la difficulté de la définition de la température.

Notes et références

Notes

Expression valide dans le cas d'une transformation réversible.
Expression valide dans le cas d'une transformation isochore.
Mais pas sur l'équation d'état dont la justification relève de l'approche microscopique.
On peut également utiliser l'enthalpie au lieu de l'énergie interne.

Références

(en) William Thomson, « On an absolute thermometric scale founded on Carnot's theory of the motive power of heat and calculated from Regnaut's observations », Philosophical Magazine, vol. 33,‎ 1848.
(en) J. Robison, Lectures on the Elements of Chemistry by Joseph Black, Longman and Rees, 1803 (lire en ligne [PDF]).
(de) Rudolf Clausius, « Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen », Annalen der Physik, vol. 155, n^o 3,‎ 1850, p. 368–397 (DOI 10.1002/andp.18501550306).
(en) Paul Ehrenfest et Tatiana Ehrenfest (trad. de l'allemand), The Conceptual Foundations of the Statistical Approach in Mechanics, New York, Dover, 1990, 114 p. (ISBN 0-486-66250-0, lire en ligne).
M. Henry, « Échelle de Kelvin ».
(en) S. Chandrasekhar, An Introduction to the Study of Stellar Structure, Dover, 1939, 512 p. (ISBN 978-0-486-60413-8, lire en ligne).
(en) Joseph Oakland Hirschfelder, Charles Francis Curtiss et Robert Byron Bird, Molecular Theory of Gases and Liquids, John Wiley and Sons, 1966 (ISBN 978-0-471-40065-3).
(en) Ludwig Boltzmann (trad. de l'allemand), Lectures on Gas Theory, New York, Dover, 1964, 490 p. (ISBN 0-486-68455-5, lire en ligne).
Joseph Fourier, Théorie analytique de la chaleur, Firmin Didot, 1822 (lire en ligne).
(en) A. E. Leanhardt, T. A. Pasquini, M. Saba, A. Schirotzek, Y. Shin, D. Kielpinski, D. E. Pritchard et W. Ketterle, « Cooling Bose-Einstein Condensates Below 500 Picokelvin », Science, vol. 301, n^o 5639,‎ 2003, p. 1513-1515.
D. Ivanov, « Cours ETH Zurich : Physique statistique I ».
Le Système international d’unités (SI), Bureau international des poids et mesures, 2019, 2019^e éd., 109 p. (présentation en ligne, lire en ligne [PDF]), p. 21.
(en) Joachim Oxenius, Kinetic Theory of Particles and Photons : Theoretical Foundations of Non-LTE Plasma Spectroscopy, Springer Verlag, coll. « Springer Series in Electrophysics », 1986, 356 p. (ISBN 978-3-642-70728-5, lire en ligne).
(en) R. Brun, Introduction to Reactive Gas Dynamics, Oxford University Press, 2009 (ISBN 978-0-19-955268-9, lire en ligne).
(en) « O. V. Lounasmaa Laboratory of Aalto University : Positive and negative picokelvin temperatures ».
(en) Norman Foster Ramsey, « Thermodynamics and Statistical Mechanics at Negative Absolute Temperatures », Physical Review, vol. 103, n^o 1,‎ 1965, p. 20-27 (lire en ligne [PDF]).
(en) J. Dunkel et S. Hilbert, « Consistent thermostatistics forbids negative absolute temperatures », Nature Physics, vol. 10,‎ 2014, p. 67-72 (DOI 10.1038/nphys2815).

Voir aussi

Articles connexes

Chaleur

Portail de la physique
Portail de la chimie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Expression valide dans le cas d'une transformation réversible.

[2] Expression valide dans le cas d'une transformation isochore.

[9] Mais pas sur l'équation d'état dont la justification relève de l'approche microscopique.

[10] On peut également utiliser l'enthalpie au lieu de l'énergie interne.

[3] (en) William Thomson, « On an absolute thermometric scale founded on Carnot's theory of the motive power of heat and calculated from Regnaut's observations », Philosophical Magazine, vol. 33,‎ 1848.

[4] (en) J. Robison, Lectures on the Elements of Chemistry by Joseph Black, Longman and Rees, 1803 (lire en ligne [PDF]).

[5] (de) Rudolf Clausius, « Ueber die bewegende Kraft der Wärme und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen », Annalen der Physik, vol. 155, n^o 3,‎ 1850, p. 368–397 (DOI 10.1002/andp.18501550306).

[6] (en) Paul Ehrenfest et Tatiana Ehrenfest (trad. de l'allemand), The Conceptual Foundations of the Statistical Approach in Mechanics, New York, Dover, 1990, 114 p. (ISBN 0-486-66250-0, lire en ligne).

[7] M. Henry, « Échelle de Kelvin ».

[8] (en) S. Chandrasekhar, An Introduction to the Study of Stellar Structure, Dover, 1939, 512 p. (ISBN 978-0-486-60413-8, lire en ligne).

[H-11] (en) Joseph Oakland Hirschfelder, Charles Francis Curtiss et Robert Byron Bird, Molecular Theory of Gases and Liquids, John Wiley and Sons, 1966 (ISBN 978-0-471-40065-3).

[12] (en) Ludwig Boltzmann (trad. de l'allemand), Lectures on Gas Theory, New York, Dover, 1964, 490 p. (ISBN 0-486-68455-5, lire en ligne).

[13] Joseph Fourier, Théorie analytique de la chaleur, Firmin Didot, 1822 (lire en ligne).

[14] (en) A. E. Leanhardt, T. A. Pasquini, M. Saba, A. Schirotzek, Y. Shin, D. Kielpinski, D. E. Pritchard et W. Ketterle, « Cooling Bose-Einstein Condensates Below 500 Picokelvin », Science, vol. 301, n^o 5639,‎ 2003, p. 1513-1515.

[15] D. Ivanov, « Cours ETH Zurich : Physique statistique I ».

[16] Le Système international d’unités (SI), Bureau international des poids et mesures, 2019, 2019^e éd., 109 p. (présentation en ligne, lire en ligne [PDF]), p. 21.

[17] (en) Joachim Oxenius, Kinetic Theory of Particles and Photons : Theoretical Foundations of Non-LTE Plasma Spectroscopy, Springer Verlag, coll. « Springer Series in Electrophysics », 1986, 356 p. (ISBN 978-3-642-70728-5, lire en ligne).

[18] (en) R. Brun, Introduction to Reactive Gas Dynamics, Oxford University Press, 2009 (ISBN 978-0-19-955268-9, lire en ligne).

[19] (en) « O. V. Lounasmaa Laboratory of Aalto University : Positive and negative picokelvin temperatures ».

[20] (en) Norman Foster Ramsey, « Thermodynamics and Statistical Mechanics at Negative Absolute Temperatures », Physical Review, vol. 103, n^o 1,‎ 1965, p. 20-27 (lire en ligne [PDF]).

[21] (en) J. Dunkel et S. Hilbert, « Consistent thermostatistics forbids negative absolute temperatures », Nature Physics, vol. 10,‎ 2014, p. 67-72 (DOI 10.1038/nphys2815).