Ludwig Boltzmann
Ludwig Eduard Boltzmann (né le à Vienne, Autriche et mort le à Duino) est un physicien et philosophe autrichien. Il est considéré comme le père de la physique statistique et un fervent défenseur de l’existence des atomes[1]. Validant l’hypothèse de Démocrite selon laquelle « la matière peut être considérée comme un ensemble d'entités indivisibles », Boltzmann, à l'aide de son équation cinétique dite « de Boltzmann », a théorisé de nombreuses équations de mécanique des fluides et de théorie cinétique des gaz.
« Boltzmann » redirige ici. Pour le cratère, voir Boltzmann (cratère).

| Naissance | |
|---|---|
| Décès | |
| Sépulture | |
| Nom dans la langue maternelle |
Ludwig Eduard Boltzmann |
| Nom de naissance |
Ludwig Eduard Boltzmann |
| Nationalité | |
| Domicile | |
| Formation | |
| Activités | |
| Conjoint |
Henriette Boltzmann (d) |
| Enfants |

Biographie
Enfance et adolescence
Ludwig Eduard Boltzmann naît à Vienne, capitale de l'Empire d'Autriche, la nuit du 19 au , entre le mardi-gras et le mercredi des Cendres. Boltzmann ironisera sur les circonstances de sa naissance qui seraient la cause de sa bipolarité, passant de moments d'enthousiasme à des moments de profonde dépression (p. 5)[2]. Son père, Ludwig Georg, est percepteur à Vienne et sera par la suite muté à Wels puis à Linz où il finira inspecteur en chef du Trésor impérial dans cette ville. Son grand-père paternel, originaire de Berlin, est horloger et fabricant de boites à musique à Vienne (p. 5)[2]. Sa mère, Katharina Maria Pauernfeind, est issue d'une famille de commerçants aisés de Salzbourg. Elle est arrière petite-fille de Johann Christian Paurnfeind, maire de Salzbourg de 1755 à sa mort en 1768. Ludwig a un frère, Albert, né en 1845, et une sœur, Hedwig, née en 1848 (p. 17)[3].
Les enfants Boltzmann reçoivent une éducation primaire à domicile par un précepteur. Ils bénéficient aussi des cours d'un professeur de musique. Ludwig apprécie la musique et sera pendant toute sa vie un excellent pianiste (p. 18)[3]. Les garçons font leurs études secondaires au lycée de Linz lorsque leur père meurt en 1859. Leur mère prend un soin particulier à ce que ses fils poursuivent leurs études, surtout qu'ils se révèlent tous deux particulièrement brillants. Grâce à sa fortune personnelle, elle peut subvenir aux besoins de sa famille (p. 34)[3]. Le , Albert meurt, probablement de tuberculose. Ludwig est très affecté par la mort de son frère dont il était très proche. En juillet de la même année, il passe le baccalauréat avec la mention "Très Bien" et est admis à suivre les cours de Mathématiques et de Physique à l'Université de Vienne. La famille déménage à Vienne (p. 37)[3].
Étudiant à l'Université de Vienne (1863-1869)
En , Boltzmann commence ses études à l'Université de Vienne. Il a Joseph Petzval pour professeur de Mathématiques, Josef Stefan et Andreas von Ettingshausen pour professeurs de Physique. En 1864, Boltzmann reçoit une bourse de recherche et commence ses travaux sous la direction de Stefan à l'Institut de Physique. L'Institut de Physique de l'Université de Vienne a été fondé en 1849 par Christian Doppler (1803-1853). Il est alors dirigé par von Ettingshausen. En 1865, Boltzmann publie son premier article scientifique sur Le mouvement de l'électricité sur les surfaces courbes. Son deuxième article, paru en 1866, intitulé Importance mécanique du second principe de la thermodynamique, amorce les recherches qui occuperont toute sa vie et assureront sa réputation (p. 41)[3]. Cette publication peut être considérée comme sa thèse de doctorat bien que l'Université de Vienne n'ait institué le doctorat qu'en 1872 (p. 6)[2]. La même année, Josef Stefan prend la direction de l'Institut de Physique et propose à Boltzmann un poste de professeur-assistant. Les quelques années passées à l'Institut, dans une ambiance studieuse et enthousiaste, marquent Ludwig Boltzmann qui s'en souviendra comme d'une période heureuse et féconde :
- « Ainsi, l'Institut, installé à l'époque rue Erdberg, était la preuve que de grandes victoires pouvaient être obtenues dans de petits locaux d'enseignement. D'ailleurs, tout au long de mon existence, je n'ai cessé de considérer Erdberg comme le symbole d'une activité expérimentale sérieuse et ingénieuse. Quand j'ai réussi à insuffler un peu de vie à l'Institut de Physique de Graz, je l'appelais "le petit Erdberg". Il n'avait rien de petit puisqu'il était deux fois plus grand que celui de Stefan, mais je n'étais pas encore parvenu à y recréer l'esprit de l'Institut de la rue Erdberg. » (Éloge funèbre de Boltzmann à Josef Stefan (p. 38)[3])
Au cours de l'année scolaire 1867-1868, Boltzmann reçoit la venia legendi, l'équivalent de l'agrégation, qui lui donne le droit d'enseigner. Il donne ses premiers cours à l'université sur les principes de la théorie mécanique de la chaleur. En 1868, il publie son troisième article intitulé Étude sur l'équilibre de la force vive de points matériels en mouvement.

À l'Institut de la rue Erdberg, Boltzmann est particulièrement influencé par deux personnalités : Josef Stefan et Johann Josef Loschmidt. Stefan avait une grande culture scientifique et était aussi poète. Il s'intéressait à tous les développements touchant la Physique, de l'électromagnétisme à la thermodynamique. Il avait une grande estime pour James Clerk Maxwell dont il a fait connaître les travaux à son assistant Boltzmann (p. 40)[3]. C'est Stefan qui formula en 1879, sur des bases expérimentales, la loi qui porte son nom et relie l'énergie rayonnée par un corps noir à sa température. C'est Boltzmann qui donnera en 1884 la démonstration théorique de la loi de Stefan qui deviendra ainsi la loi de Stefan-Boltzmann. Et c'est logiquement que, à la mort de Stefan en 1890, l'Université de Vienne offre la chaire de Physique mathématique à Boltzmann, son plus brillant élève.

Le second personnage qui influence Boltzmann est Johann Josef Loschmidt. Loschmidt était diplômé en Physique et en Chimie de l'Université de Vienne en 1846. Il avait 23 ans de plus que Boltzmann. Comme il n'avait pas pu obtenir de poste d'enseignant, il avait passé 20 ans dans diverses activités industrielles de chimie. À la suite de la faillite de son entreprise, il rejoint l'Institut de Physique en 1866. Loschmidt devient assistant-professeur en 1868, puis professeur de Chimie physique en 1872 à l'Université de Vienne. Parmi ses recherches éclectiques, il donna en 1865 la première approximation du nombre de molécules d'air par unité de volume. Il estima qu'il y avait 1,81 × 1024 molécules par m3 d'air. Ce nombre fut ré-estimé à 1,9 × 1025 par Maxwell qui l'appela constante de Loschmidt (p. 45)[3]. Amedeo Avogadro avait émis l'idée selon laquelle le volume d'une certaine quantité d'un gaz devait être proportionnel au nombre de molécules contenues dans ce volume. En 1909, Jean Perrin[4] a calculé le nombre de molécules contenues dans une mole de gaz et l'a appelé Nombre d'Avogadro : NA = 6,02 × 1023. Sachant qu'une mole de gaz occupe 22,4 litres dans les conditions normales de température et de pression, la constante de Loschmidt est égale à L = 2,69 × 1025 m−3. Cette découverte de Loschmidt fut très importante pour le jeune Boltzmann. Elle consolida ses conceptions atomistes et son approche probabiliste de sa théorie de la chaleur. Boltzmann et Loschmidt furent bons amis, ce qui n'empêcha pas Loschmidt de critiquer vigoureusement la première tentative de Boltzmann de traiter de façon cinétique le second principe de la thermodynamique. Cette critique obligera Boltzmann a approfondir son approche statistique de l'entropie (p. 64)[3].
Voici ce qu'écrit Boltzmann de ses deux mentors à l'Institut de physique :
- « Parce qu'ils étaient sans prétention aucune, de par leur simplicité et leur modestie, ils se ressemblaient beaucoup. Ils n'essayaient jamais de faire montre de leur supériorité intellectuelle. Pendant les longues années que je passai auprès d'eux, d'abord comme étudiant, puis comme assistant, ils me traitèrent toujours comme un ami. Leur sérénité olympienne et leur humour si fin, qui faisaient des discussions les plus âpres un divertissement ludique pour les étudiants, me marquèrent au point d'influencer ma manière d'être. (p. 41)[3] »
Professeur de physique mathématique à Graz (1869-1873)

La chaire de Physique mathématique est devenue vacante à l'Université de Graz lorsque son titulaire, Ernst Mach, est parti pour l'Université Charles de Prague en 1867. Sur recommandation de Stefan et avec l'appui d'August Toepler, professeur de Physique expérimentale à Graz, Ludwig Boltzmann est nommé par l'empereur François-Joseph à la chaire de Physique mathématique de l'Université de Graz à l'âge de 25 ans. Boltzmann et Toepler s'entendent bien. Ils publient plusieurs travaux réalisés en collaboration. Toepler est un homme entreprenant qui lance la construction d'un nouveau bâtiment de laboratoires de Physique (p. 6)[2] et qui trouve l'argent pour l'équiper (p. 13)[2]. Boltzmann s'épanouit à Graz. Ses cours sont appréciés. Son travail de recherche avance. Son salaire est rapidement et considérablement augmenté (p. 53)[3]. Cependant, il se rend compte qu'à Vienne ses maîtres Stefan et Loschmidt travaillaient en vase clos, ne se déplaçaient pas et ne participaient pas aux rencontres internationales, ce qui nuisait à leur travail et à leur notoriété. Pour ne pas reproduire ces travers, il demande à l'Université l'autorisation de s'absenter pour visiter des collègues en Allemagne, autorisation qui lui est accordée.
En avril-, il se rend à Heidelberg pour visiter le chimiste Robert Bunsen. Au cours de ce séjour, il assiste à un séminaire du mathématicien Leo Königsberger pendant lequel il propose une solution à un problème présenté comme impossible à résoudre. Après une discussion dans le bureau de Königsberger, celui-ci l'incite à rencontrer le très célèbre physicien Gustav Kirchhoff (p. 53)[3]. Boltzmann se présente donc dans le laboratoire de Kirchhoff et, au cours de leur échange, il lui signale une erreur dans l'un de ses articles. Kirchhoff est d'abord très mécontent de se faire corriger par un jeune homme inconnu, autrichien de surcroît, mais il reconnaît son erreur et apprécie la franchise et l'acuité intellectuelle de son visiteur. Les deux hommes garderont une estime réciproque et resteront en relation professionnelle et amicale (p. 54)[3].

Pendant le semestre d'hiver 1871-1872, Boltzmann visite Hermann von Helmholtz à l'Université Friedrich Wilhelm à Berlin. Ses entretiens avec Helmholtz sur la Physique et les Mathématiques sont très enrichissants pour Boltzmann, mais la froideur et ce qu'il juge être l'arrogance d'Helmholtz tempèrent son enthousiasme (p. 54)[3]. Il déclare un jour qu'« il y a des problèmes dont je ne peux parler qu'avec Helmholtz mais il est trop distant (p. 10)[2]. » De retour à Graz, il publie un de ses articles les plus importants : Nouvelles études sur l'équilibre thermique des molécules gazeuses. C'est dans cette publication que l'équation de Boltzmann est introduite. Elle décrit les propriétés statistiques d'un gaz constitué de molécules et, d'un point de vue historique, c'est la première équation qui décrit l'évolution temporelle d'une probabilité (p. 7)[2].
En 1872, Boltzmann intervient en faveur d'une brillante étudiante de l'École Normale de Graz, Henriette von Aigentler, qui veut suivre les cours de Mathématiques et de Physique, mais à qui l'Université interdit l'accès parce qu'elle est une femme. Bien que l'intervention de Boltzmann soit partiellement infructueuse, Ludwig et Henriette restent en contact épistolaire, car Ludwig part à Vienne (p. 67)[3]. Ils se marieront en 1876 quand Ludwig revient à Graz. Henriette est née le à Stainz. Son père, avocat, est mort en 1854 et sa mère en 1873. L'orpheline est adoptée par le maire de Graz, Wilhelm Kienzl, le père du compositeur Wilhelm Kienzl (p. 71)[3]. Elle est la première femme à suivre les cours de Mathématiques, Physique et Philosophie à l'Université de Graz comme auditrice extraordinaire. Dans une de ses lettres, Boltzmann exprime combien il est important pour lui que son épouse soit capable d'apprécier et de partager ses préoccupations scientifiques :
- « S'il est vrai que, pour un mari dont le seul capital est son propre travail, les vertus d'une maîtresse de maison sobre et rigoureuse et d'une bonne mère de famille sont essentielles, il me semble qu'on ne peut parler d'amour durable si son épouse ne montre ni compréhension ni enthousiasme devant les efforts de son travail et qu'elle se contente d'être sa servante et non la compagne qui lutte à ses côtés (p. 68)[3]. »
Professeur de mathématiques à Vienne (1873-1876)
En 1873, la chaire de Mathématiques de l'Université de Vienne se libère. Boltzmann présente sa candidature appuyée par Stefan. Bien que classé 3e dans un premier temps, il obtient le poste (p. 68)[3]. Il donne des cours de Mathématiques, mais aussi de Physique et continue son travail de recherche en Thermodynamique. En 1875, l'École Polytechnique Fédérale de Zurich lui propose un poste de professeur permanent. Boltzmann en informe le Ministère qui, immédiatement augmente son salaire et les moyens mis à sa disposition pour le garder. À cette époque, l'Université de Fribourg-en-Brisgau lui fait aussi une proposition. Mais Boltzmann a d'autres projets : en , il propose formellement à Henriette de l'épouser.

Professeur de physique expérimentale à Graz (1876-1890)
August Toepler qui dirigeait l'Institut de Physique de Graz n'était pas satisfait des conditions de recherche à Graz. Il décida donc de partir pour l'École Polytechnique Saxonne de Dresde (p. 71)[3]. Boltzmann propose sa candidature pour lui succéder comme professeur de Physique expérimentale et directeur de l'Institut de Physique tout neuf et bien équipé. Sa nomination à Graz serait d'autant plus opportune qu'il se marie avec Henriette à Graz le . Mais Ernst Mach, un physicien expérimental reconnu, est aussi candidat. Mach a fait ses études avec Wilhelm Kienzl, le fils du maire de Graz. Par son camarade, il est au courant des tractations en cours à l'Université au sujet de la succession de Toepler. Cependant Boltzman bénéficie des mêmes informations par son épouse Henriette qui est fille adoptive du maire et qui fait campagne en sa faveur auprès des professeurs de l'Université de Graz. Finalement, Mach retire sa candidature et laisse la place à Boltzmann (p. 72)[3].
Ludwig et Henriette furent heureux à Graz pendant une dizaine d'années bien qu'ils dussent héberger sous leur toit Katharina, la mère de Ludwig, et Hedwig, sa sœur, qui avait des problèmes de santé mentale. Ils eurent cinq enfants : Ludwig Hugo, né en 1878, Henriette, née en 1880, Arthur Ludwig, né en 1881, Ida, née en 1884, et Elsa, née à Vienne en 1891. Boltzmann était très attentif et affectueux avec ses enfants. Il disposait d'un appartement de fonction à l'Université. Il acheta une ferme dans les environs pour que ses enfants puissent vivre à la campagne et profiter de la nature. Il constitua lui-même un herbier et une collection de papillons. Il avait un chien et avait acheté une vache (p. 93)[3]. Il aimait marcher et nager l'été, et patiner l'hiver. Il prétendait faire de l'exercice physique qu'il n'avait pas pu faire dans sa jeunesse (p. 16)[2]
À Graz, il aimait recevoir et distrayait ses hôtes par sa grande culture scientifique, littéraire et musicale. C'était un bon vivant qui aimait la bonne chère et les discussions autour d'une bière. Il fut souvent invité à dîner au palais impérial. Mais il était frustré de ne pas pouvoir profiter des plats qui étaient servis, d'une part, parce que l'empereur mangeait très peu et, d'autre part, parce que sa vue défaillante ne lui permettait pas de voir dans son assiette (p. 94)[3].
Ces occupations n'empêchent pas Boltzmann de poursuivre ses recherches sur la Thermodynamique. La chaire de Physique théorique qu'il a abandonnée quelques années plus tôt est tenue par Heinrich Streintz qui ne lui fait pas ombrage et avec qui il s'entend bien. Pour l'aider, les autorités académiques créent un poste d'assistant qui est attribué à Albert von Ettingshausen, un neveu d'Andreas, qui prend en charge les questions administratives du laboratoire. Ce physicien aura une certaine célébrité en découvrant l'effet thermomagnétique (p. 15)[2]. Les critiques suscitées par son article de 1872 obligent Boltzmann à approfondir sa théorie. Ce qu'il expose dans un nouvel article en 1877, intitulé Rapport entre le second théorème de la théorie mécanique de la chaleur et le calcul des probabilités relatives aux résultats de l'équilibre thermique. Dans ce travail, il formule ce qu'Albert Einstein appellera le principe de Boltzmann, c'est-à-dire l'interprétation du concept d'entropie comme une mesure mathématiquement définie de ce qu'on appelle le désordre des atomes, qui était déjà apparu dans l'article de 1872, mais qui est étendu et devient un principe général (p. 18)[2]. Pendant l'année 1878-1879, il est nommé doyen de la faculté des arts. En 1884, il publie sa démonstration de la loi de Stefan qu'Hendrik Lorentz qualifiera de « perle de la physique théorique ». En 1885-1887, il engage un débat scientifique avec deux collègues britanniques, Peter Guthrie Tait et William Burnside. Ces échanges contribuent à sa réputation outre-Manche (p. 19)[2].

La vie à Graz, jusque-là heureuse et productive, est perturbée par la mort de Katharina Boltzmann le . La perte de sa mère, dont il était très proche depuis la mort de son père, est un choc qui plonge Boltzmann dans une profonde dépression. C'est la première manifestation sérieuse de sa bipolarité. En 1887, la nomination de Boltzmann au poste de recteur de l'Université est un honneur qui tourne rapidement à la catastrophe, car Boltzmann n'est guère diplomate et se révèle incapable de prendre de la distance vis-à-vis des personnes et des situations (p. 95)[3]. Pour Mach, « Boltzmann n'est pas méchant mais il est incroyablement naïf et informel. Il ne sait tout simplement pas imposer des limites » (p. 99)[3]. Une autre situation embarrassante se noue au même moment.
En 1887, son collègue et ami, Gustav Kirchhoff, qui avait quitté Heidelberg pour Berlin, meurt. L'année suivante, l'Université Friedrich Wilhelm de Berlin, sur proposition d'Hermann von Helmholtz, qui avait aussi quitté Heidelberg pour Berlin, propose à Boltzmann de succéder à Kirchhoff. Boltzmann se rend à Berlin, visite le laboratoire de Physique et donne son accord de principe. De retour à Graz, le doute le saisit. De plus, ses collègues, qu'il n'a pas prévenus, apprennent sa démarche par des voies détournées. L'empereur est furieux. Que le meilleur physicien autrichien parte en Allemagne relevait de la trahison. Boltzman finit par renoncer à la chaire de Berlin en prétextant de sa mauvaise santé et de sa mauvaise vue (p. 100)[3]. La chaire vacante est finalement attribuée à Max Planck. L'épisode ruine la crédibilité de Boltzmann et l'entraîne dans une nouvelle crise de dépression aggravée par deux décès successifs. En 1888, son fils aîné, Hugo, 10 ans, succombe à une appendicite non diagnostiquée à temps. En 1889, c'est sa sœur Hedwig qui meurt à 41 ans. Pour sortir de cette ambiance macabre, Boltzmann part enseigner à l'Université de Munich (p. 102)[3].
Professeur de physique théorique à Munich (1890-1894)
Une nouvelle chaire de Physique théorique est créée pour Boltzmann à l'Université Ludwig Maximilians de Munich. Il apprécie de se trouver avec des collègues d'un niveau scientifique plus élevé qu'à Graz : Adolf von Baeyer (1835-1917), futur Prix Nobel de Chimie, le physicien Carl von Linde (1842-1934), spécialiste de la cryogénie, ou l'astronome Hugo von Seeliger (1849-1924). Ses étudiants l'apprécient et certains d'entre eux, étudiants à Graz, l'ont suivi à Munich. Cependant, Boltzmann devient presque aveugle. Il dicte ses lettres et ses articles à Henriette. Il prend une secrétaire pour lui lire les articles de ses collègues. D'autre part, le gouvernement bavarois n'assure pas la retraite des universitaires. Boltzmann, qui a des problèmes de santé physique et psychique, s'inquiète pour son avenir. Il a aussi le mal du pays. Quand son maître, Josef Stefan, meurt en 1893 et que l'Université de Vienne le sollicite pour reprendre la chaire de Physique théorique, il accepte avec soulagement. Il reste encore une année à Munich puis rejoint Vienne (p. 103)[3].
En 1892, Boltzmann assiste au 300e anniversaire de Trinity College à Dublin. En 1894, l'Université d'Oxford lui confère le titre de docteur honoris causa, ce qui témoigne du prestige dont il jouit en Grande-Bretagne (p. 103)[3].
Professeur de physique théorique à Vienne (1894-1900)
De retour à Vienne en 1894, Boltzmann est déçu. Il trouve les étudiants passifs, sans initiatives ni enthousiasme. Il a l'impression d'être professeur de lycée. En 1895, une chaire d'Histoire et de Philosophie des Sciences inductives est créée pour Ernst Mach, collègue physicien de Boltzmann, qui professe d'emblée des critiques acerbes des conceptions atomistes, évolutionnistes et probabilistes de Boltzmann (p. 104)[3]. Après une conférence de Boltzmann à l'Académie des Sciences de Vienne, Mach déclare qu'il ne croit pas aux atomes. Mach est partisan d'un monde continu dans lequel la matière et l'énergie sont les deux faces de la réalité. Boltzmann supporte mal le travail de démolition dirigé contre lui par ses collègues. Il met toute son énergie à contrer ces théories et à affermir ses propres conceptions.
En 1895, lors d'un congrès à Lübeck, Wilhelm Ostwald présente une conférence intitulée Au-delà du matérialisme. Boltzmann prend vigoureusement la parole pour contrer les thèses "énergétistes" du conférencier. Arnold Sommerfeld qui assiste à l'échange le comparera plus tard à une corrida :
- « Helm, le défenseur de l'énergétique, était accompagné par Ostwald et tous deux brandissaient ensemble le bouclier de la philosophie d'Ernst Mach (qui n'était pas présent). Ils faisaient face à Boltzmann accompagné de Félix Klein. La bataille entre Boltzmann et Ostwald paraissait un duel entre un taureau et un torero très adroit. Cependant, cette fois, le taureau vainquit le toréador, malgré l'adresse de ce dernier.Les arguments de Boltzmann donnèrent dans le mille. Tous les jeunes mathématiciens, dont je faisais partie, étaient rangés derrière Boltzmann. Pour nous, on ne pouvait déduire d'une seule équation de l'énergie les équations du mouvement d'un point matériel et encore moins d'un système constitué d'un nombre arbitraire de degrés de liberté. Je dois tout de même signaler, à la décharge d'Ostwald, le commentaire qui figure dans son livre Grosse Männer (Leipzig, 1909, p.405) où il appelle Boltzmann l'homme dont la science nous a dépassés par sa perspicacité et sa clarté (p. 108)[3]. »
Cette dernière remarque peut être interprétée de deux façons. D'une part, malgré l’âpreté du combat intellectuel entre atomistes et énergétistes, Boltzmann garda des rapports courtois avec ses adversaires. D'autre part, en 1909, compte tenu des travaux de Max Planck (1900) et d'Albert Einstein (1905), il apparaissait qu'effectivement Boltzmann avait été très perspicace en 1895.
Alors que le contexte lui est hostile à Vienne et qu'il est ignoré en France, Boltzmann est connu et reconnu dans les pays anglo-saxons[5]. Il est nommé membre étranger de la Royal Society en 1899. La même année il est invité à l'Université Clark à Worcester, Massachusetts. Il s'y rend accompagné d'Henriette (p. 28)[2]. L'université Clark lui confère un diplôme d'honneur. Il y donne une série de quatre cours [6]. Au cours de ce premier voyage d'un mois aux États-Unis, les Boltzmann visitent Boston, Pittsburgh, Washington, Baltimore et Philadelphie ainsi que Montréal.
À son retour à Vienne, il accepte l'offre d'Ostwald de venir enseigner à Leipzig et part sans même prévenir ses collègues viennois (p. 120)[3].
Professeur de physique théorique à Leipzig (1900-1902)
Bien qu'Ostwald soit un adversaire intellectuel dont les conceptions philosophiques sont proches de celles de Mach, Boltzmann juge qu'il lui faut sortir de son combat obsessionnel avec Mach et s'éloigner de Vienne. Il débute ses cours à Leipzig le . Il n'est pas bien. Il a peur de perdre la mémoire et appréhende d'entrer dans l’amphithéâtre. Il est parfois obligé d'annuler ses cours. Pour se distraire, il effectue une croisière en Méditerranée avec son fils Arthur pendant l'été 1901. Mais il souffre de la chaleur et rentre fatigué. Il déprime et fait une tentative de suicide. Il est soigné à l'hôpital psychiatrique par le docteur Paul Flechsig. Son état dépressif est de notoriété publique. La situation est telle que lorsqu'une occasion se présente de retourner à Vienne, les Boltzmann n'hésitent pas.
Professeur de physique théorique et professeur de philosophie à Vienne (1902-1906)
Ernst Mach ayant pris sa retraite en 1901 à la suite d'un accident vasculaire cérébral, Boltzmann manifeste son désir de revenir à Vienne. Mais l'Empereur François-Joseph se montre réticent à redonner une chaire à un homme qui a quitté ses fonctions et l'Autriche quelques années plus tôt dans des conditions peu correctes (p. 121)[3]. Ses collègues viennois, connaissant son état psychique fragile, doutent qu'il puisse assumer ses fonctions de professeur. Boltzmann prend des vacances en famille au bord de la mer et retrouve un certain équilibre. Finalement, il est accepté et reprend ses cours de Physique théorique à Vienne en . L'année universitaire se passe bien. Il passe à nouveau l'été au bord de la mer où il prépare activement ses cours. À la rentrée 1903, il prend en charge la chaire de Philosophie et d'Histoire des Sciences qui était vacante depuis le départ de Mach. Ses cours de Philosophie (deux heures par semaine) ont un énorme succès. Il n'y a pas assez de places dans l'amphithéâtre pour accueillir tous ceux qui veulent l'entendre. Il retrouve l'estime et la bienveillance de l'Empereur qui l'invite à nouveau au palais. Il savoure sa revanche sur Ernst Mach (p. 117)[3]. En 1903 il fonde avec Gustav von Escherich et Emil Müller la Société mathématique autrichienne.
Boltzmann s'investit dans ses cours de Philosophie et dans la rédaction de ses conférences de Physique. Il ne produit plus de travail de recherche original. Il assiste à des congrès en Allemagne, en Angleterre et à Paris. Cependant, la majorité de ses collègues physiciens sont anti-atomistes et jugent ses travaux "démodés", car ancrés dans l'atomisme de Démocrite. Pour Mach, Boltzmann est « le dernier pilier de l'atomisme (p. 107)[3] ». En 1904, il entreprend son deuxième voyage en Amérique pour se rendre au congrès de Mathématiques de Saint-Louis. Il est accompagné de son fils Arthur. Sa communication est classée dans la section de Physique appliquée. Boltzmann constate qu'on l'a écarté de la section de Physique théorique, qu'il considère comme sienne. Il en est humilié. Entre la fin août et le début octobre, il visite Detroit et Chicago. Malgré la fatigue du voyage, il reprend ses cours aussitôt son retour à Vienne.

En , il est invité à Berkeley pour une école d'été. Il retraverse l'Atlantique sur le Kronprinz Wilhelm au départ de Brême. Il traverse les États-Unis de New York à San Francisco en 4 jours et 4 nuits de train. Il donne à Berkeley une série de 30 cours qui sont moyennement appréciés par les étudiants du fait de son peu de maîtrise de l'anglais (p. 127)[3]. Boltzmann est vivement intéressé et impressionné par sa visite du Lick Observatory. Il effectue le voyage de retour sur le Kaiser Wilhelm II. Ce voyage a dû lui plaire, car, au retour, il en fait un récit humoristique intitulé : Voyage d'un professeur allemand en Eldorado (p. 31)[2]. Boltzmann est de nouveau de bonne humeur et a retrouvé sa forme (p. 126)[3]. Mais, début , il a un nouvel accès de neurasthénie sévère. Il est très corpulent, pratiquement aveugle et souffre d'insuffisance rénale et d'angine de poitrine. Il est paralysé par la peur d'entrer en cours. Il est obligé d'arrêter ses cours qui sont repris par Stefan Meyer. Ernst Mach écrit :
- « Boltzmann allait donner des cours pendant le semestre d'été, mais il dut les annuler, probablement en raison de sa maladie nerveuse. On savait dans les cercles informés que Boltzmann ne pourrait probablement plus jamais faire cours. On entendait dire qu'il devait être placé sous surveillance médicale constante, car il avait déjà essayé de se donner la mort. » (p. 129)[3]
Pendant l'été, Henriette prend l'initiative de l'emmener en vacances au bord de la mer Adriatique à Duino, près de Trieste, alors en territoire austro-hongrois. Le , pendant qu'elle est à la plage, Boltzmann se suicide. Sa fille Elsa, 15 ans, le trouve pendu dans sa chambre d'hôtel. Il n'a laissé aucune note explicative de son geste (p. 125)[3]. Boltzmann est enterré quelques jours plus tard à Vienne. Sa mort est une grosse déception pour les étudiants qui s’apprêtaient à suivre ses cours. Parmi eux, Ludwig Wittgenstein qui finissait le lycée à Linz et se proposait d'assister aux cours de Boltzmann à Vienne. Il choisit alors de faire des études d'ingénieur à Berlin (p. 130)[3].
Boltzmann laisse une épouse et quatre enfants. Henriette Boltzmann lui survivra 32 ans. Elle meurt à Vienne le . Sa fille Henriette, enseignante célibataire, meurt le . Arthur Ludwig, physicien et ingénieur, aura 3 enfants. Il meurt le . Ida, étudiante en Mathématiques et Physique, meurt à 25 ans le . Elsa, formée en Suède pour devenir physiothérapeute, épouse en 1920 le physicien Ludwig Flamm, ancien étudiant de son père. Ils auront 4 enfants. Elle meurt le .
Boltzmann professeur
Professeur de mathématiques et professeur de physique
Boltzmann a beaucoup bougé géographiquement et, semble-t-il, thématiquement. Il a tour à tour occupé des chaires de Mathématiques ou de Physique Théorique ou de Physique expérimentale. En fait, c'était un excellent mathématicien et un excellent physicien dont la vraie vocation était la Physique théorique. Mais, à la différence d'Einstein qui faisait uniquement des expériences de pensée, Boltzmann était aussi un bon expérimentateur, ce qui rendait ses cours particulièrement attractifs (p. 68)[3].
Alors qu'il n'était que professeur-assistant à Vienne en 1868-1870, il donnait des cours sur la théorie mécanique de la chaleur, la théorie de l'élasticité, la théorie mathématique de l’acoustique et la théorie mathématique de la capillarité. À Graz il enseigna le calcul différentiel et intégral, la théorie des nombres, la géométrie analytique, la théorie des fonctions, mais aussi la théorie mécanique de la chaleur. À Vienne, « il donna un cours qui dura 4 ans. Il comprenait la mécanique classique, l'hydrodynamique, la théorie de l'élasticité, l'électrodynamique et la théorie cinétique des gaz (Lise Meitner, (p. 38)[2]). »
Professeur brillant et apprécié

Boltzmann était très apprécié comme professeur. Il intéressait ses étudiants et leur communiquait sa passion pour la matière enseignée. Ses cours étaient extrêmement clairs. Lise Meitner, première femme à avoir obtenu un doctorat à l'Université de Vienne et découvreuse de la fission nucléaire, qui suivit ses cours de 1902 à 1905, en a gardé un souvenir lumineux:
- « Il avait l'habitude d'écrire les équations principales sur un tableau très large. Sur le côté il y avait deux tableaux plus petits sur lesquels il inscrivait les étapes intermédiaires. Tout était écrit sous une forme claire et bien organisée. J'avais souvent l'impression qu'on pouvait reconstruire la totalité du cours à partir de ce qui était inscrit sur les tableaux. [...] C'était un professeur brillant, dont les cours étaient les plus admirables et les plus stimulants qui soient. Il faisait montre d'un tel enthousiasme pour les connaissances qu'il transmettait que nous avions le sentiment d'un nouveau monde se dévoilant à nos yeux après chaque cours (p. 38)[2](p. 69)[3]. »
Sa réputation était telle que les étudiants d'autres disciplines venaient assister à ses cours. Franz Skaupy, qui était un industriel célèbre en Autriche, avait assisté à ses cours en 1902-1904: « La salle était toujours pleine car, parmi les élèves, il y avait non seulement les physiciens, mais aussi les chimistes comme moi (p. 70)[3]. »
La disparition prématurée de Boltzmann a été une grosse déception pour Erwin Schrödinger. En 1929, il déclara que les théories de Boltzmann avaient été son premier amour en sciences et que « personne n'avait réussi à le captiver à ce point (p. 130)[3]. »
Il pimentait ses cours de remarques, d'anecdotes ironiques parfois virulentes sur ses confrères ou sur lui-même. Il était très chaleureux envers ses étudiants, à tel point qu'à la fin, il avait beaucoup de mal à refuser un candidat aux examens. Il entretenait une correspondance avec beaucoup de ses étudiants et de ses collègues. Il a notamment correspondu fréquemment avec Svante Arrhenius, prix Nobel de Chimie 1903 (p. 71)[3].
Nous disposons du précieux témoignage d'un auditeur étranger de Boltzmann à Munich. Il s'agit d'une lettre d'Hantaro Nagaoka au Journal des Sciences de Tokyo, datée d', bien que les faits rapportés semblent s'être déroulés en 1890, à l'arrivée de Boltzmann à Munich. À cette époque, Nagaoka avait 26 ans. Il deviendra professeur à Tokyo en 1901 et sera un ardent promoteur de la recherche en Physique au Japon.
- « Munich est appelée cité des arts, tout comme notre Kyoto. Bien qu'il ne s'y passe en général rien de spécial en sciences, je m'y suis rendu début avril pour suivre les cours du professeur Boltzmann qui venait d'arriver. Heureusement, il va donner ses fameux cours sur la "Théorie cinétique des gaz" et sur "l'Application du principe d'Hamilton à la Physique". Nous avons entendu dire que le professeur Boltzmann avait été invité à Berlin pour succéder à Kirchhoff mais qu'il n'avait pas accepté l'invitation et qu'il avait choisi Munich. Je ne sais pas pourquoi il a fait cela. Je pense que personne n'est aussi compétent que lui, à part peut-être Helmholtz. Ses cours sont extrêmement clairs. Il parle distinctement, pas comme Helmholtz qui parle de façon un peu bizarre. Mais c'est un type un peu excentrique qui, parfois, finit par faire des choses stupides.[...] Le professeur Boltzmann est d'origine autrichienne. Mais il admire Maxwell et prend la position de Maxwell en de nombreuses occasions. Cette situation est confortable pour moi puisque j'ai été formé dans la tradition britannique. Je suis spécialement intéressé par la Théorie des Gaz qui a été développée par lui, Clausius et Maxwell. En particulier, à partir des cours de Boltzmann lui-même, je peux vraiment comprendre la doctrine de distribution de l'énergie de Maxwell-Boltzmann qui a fait récemment l'objet de controverses. (p. 25)[2] »
Le même Nagaoka écrit à un collègue:
- « Le professeur Bol est un homme à la barbe buissonneuse comme vous le savez. Les étudiants sont très impressionnés par son aspect. Mais ses cours sont incroyablement clairs contrairement à ceux du professeur Hel. Il semble avoir un cerveau exceptionnel car il a exposé sans note les fonctions Hamiltonniennes et les intégrales du 6ème ordre. [...] Le professeur Bol est sympathique et honnête. Il a une personnalité qui le fait aimer des étudiants contrairement à ce que son apparence laisserait supposer (p. 26)[2]. »
Œuvre scientifique de Ludwig Boltzmann
Boltzmann a travaillé dans presque tous les domaines de la physique du XIXe siècle. La majeure partie de sa production scientifique porte sur l'analyse du phénomène de la chaleur comme résultant de l'agitation aléatoire des atomes ou des molécules. Mais il a abordé aussi d'autres domaines.
Théorie cinétique des gaz et équation de Boltzmann
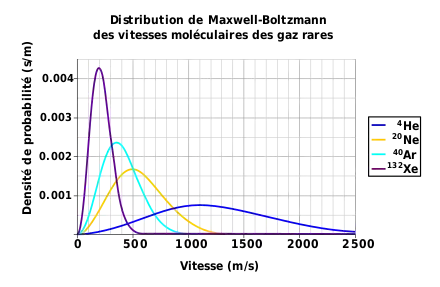
Pour l'étude des mouvements des corps, Isaac Newton, à la suite de Galilée, avait essentiellement utilisé la notion de force qui agit de l'extérieur pour modifier le mouvement. Descartes avait introduit la notion de moment, prenant en compte la masse et la vitesse d'un objet. Huyghens, en 1669, puis Leibnitz, en 1695, formulent le concept d'énergie cinétique (Force vive, vis viva), opposée à l' l'énergie potentielle (Force morte, vis mortua).
Les bases de la théorie cinétique des gaz ont été posées par Daniel Bernoulli dans son ouvrage Hydrodynamica publié en 1738. Bernoulli considérait qu'un gaz consiste en un grand nombre de molécules bougeant dans toutes les directions et dont les impacts sur les parois du récipient constituent la pression du gaz. Il considérait aussi que la température n'est que le reflet de l'énergie cinétique des molécules du gaz. Ces conceptions révolutionnaires n'ont pas eu d'écho immédiat. À la fin du XVIIIe, Benjamin Thomson, qui perçait des canons pour l'Electeur de Bavière, constate que l'opération dégage beaucoup de chaleur. Il en déduisit qu'une partie du travail mécanique est transformée en chaleur, ce qu'il interpréta comme la transformation d'un travail (déplacement de forces) à l'échelle macroscopique en une agitation désordonnée de particules de matière à l'échelle microscopique. Il posa ainsi les bases de l'équivalence entre la chaleur et le travail qui furent quantifiées et publiées par Joule en 1843.
En 1856, August Krönig esquissa un premier modèle de la théorie des gaz en considérant uniquement les mouvements de translation des molécules. En 1857, Rudolf Clausius, indépendamment de Krönig, développa sa propre théorie qui prenait en compte non seulement les mouvements de translation, mais aussi les vibrations et les rotations des molécules. Il introduisit aussi, en 1858, le concept de libre parcours moyen d'une particule (p. 77)[2]. En 1860, James Clerk Maxwell, après avoir lu le travail de Clausius, établit la loi de distribution des vitesses des molécules, qui donne la proportion des molécules ayant une vitesse comprise dans une certaine fourchette, dans un système en équilibre thermique [7],[8]. Il estime que peu de molécules sont au repos à cause des nombreuses collisions et que peu de molécules ont des vitesses très élevées, car elles n'ont qu'une énergie limitée. On doit donc s'attendre à ce que la majorité des molécules de gaz se déplacent à une vitesse proche de la valeur moyenne et que leur nombre diminue lorsque l'on s'éloigne de cette valeur moyenne. Maxwell en déduisit que la distribution des vitesses doit suivre la loi de Gauss. Il démontra aussi que les collisions moléculaires entraînent une égalisation des températures et donc favorisent l'équilibre thermique.
Boltzmann a très tôt réfléchi sur ces articles de Maxwell que Stefan lui avait recommandés. Parmi ses tout premiers travaux, il publie coup sur coup À propos du nombre d'atomes dans les molécules de gaz et de l'énergie interne dans les gaz, en 1867, et Étude sur l'équilibre de la force vive de points matériels en mouvement, en 1868. La force vive est un concept introduit par Gottfried Wilhelm Leibniz et qui signifie l'énergie cinétique (p. 58)[2]. Leibnitz introduisit aussi le principe de la conservation de la force vive dans les collisions. Puis, en 1872, Boltzmann généralise les découvertes de Maxwell dans l'article intitulé Études complémentaires sur l'équilibre thermique des molécules de gaz.
Maxwell a donné la distribution des vitesses des molécules dans un système homogène à l'équilibre thermique. Boltzmann tente de donner les équations régissant un système non homogène en évolution. Il s'agit d'un modèle cinétique dans lequel la répartition des vitesses n'est pas gaussienne dans l'espace et dans le temps. La fonction de distribution des molécules dépendra donc de 3 paramètres, le temps, la position et la vitesse.
- avant la collision, une molécule est animée d'une vitesse et l'autre molécule, d'une vitesse
- après la collision, la première est animée d'une vitesse et la seconde, d'une vitesse
L'équation de Boltzmann s'écrit alors[9] :
L'expression , appelé terme de transport libre ou d'advection, est le produit scalaire du vecteur vitesse et du vecteur gradient de f, vecteurs qui ont chacun 3 composantes spatiales. Ce terme traduit le fait que les particules circulent en ligne droite à vitesse constante entre deux collisions.
Le terme est l' intégrale de collision de Boltzmann (bilinéaire en l'inconnue ), dépendant uniquement de la vitesse (les autres variables en étant des paramètres). Elle peut s'écrire comme :
La première intégrale se développe sur , l'espace des vitesses, la seconde intégrale sur la sphère de dimension 2, l'espace des directions.
La fonction dépend du modèle. Si on considère les molécules comme des sphères dures élastiques, est proportionnelle à la norme de la différence des vitesses entre les deux particules, c'est-à-dire leur vitesse relative au moment du choc. Le facteur traduit l'angle que font leurs directions. D'autre part, les vitesses des molécules après le choc s'écrivent :
Chaque vitesse est un vecteur. Il y a donc 3 variables (dimensions) pour et et 3 variables pour et soit 6 variables. Au niveau des contraintes, si le choc est élastique, il y a conservation de la quantité de mouvement, soit 3 variables, et conservation de l'énergie cinétique, soit une variable. Les deux paramètres nécessaires à la solution sont donnés par la variable , le paramètre d'impact.
Dans la double intégrale, on a une différence de deux produits. Ces produits de probabilités viennent du fait que les variables vitesses sont aléatoires et indépendantes (chaos moléculaire) : il faut multiplier les probabilités. On multiplie donc la distribution par elle-même. D'autre part, les probabilités de distribution des molécules avant la collision (état qui disparaît) sont soustraites des probabilités de distribution des vitesses des molécules qui naissent de la collision.
Le terme de gauche de l'équation de Boltzmann est linéaire et différentiel (dérivée du premier ordre) et le terme de droite comporte une double intégrale : c'est une équation intégro-différentielle non linéaire qui donne l'évolution de la fonction de distribution des vitesses des molécules d'un gaz dilué dont les molécules sont soumises à des chocs.
Thermodynamique et mécanique statistique
Au milieu du XIXe, Rudolf Clausius avait formulé le second principe de la thermodynamique et inventé le terme entropie. L'augmentation de l'entropie dans un processus est une mesure de sa réversibilité : si l'entropie reste constante, le processus est réversible. En revanche, si elle augmente (par exemple, en mélangeant de l'eau froide avec de l'eau chaude), une inversion n'est possible qu'en fournissant de l'énergie de l'extérieur. Cependant, les lois de la mécanique classique décrivant le mouvement d'une seule particule sont invariantes par rapport au temps : pour tout mouvement d'une particule, le mouvement dans la direction opposée est aussi possible. Boltzmann a étudié le problème de savoir comment les mouvements réversibles de particules individuelles (par exemple, des atomes ou des molécules de gaz) peuvent mener à un processus global irréversible. Cette question l'a occupé tout au long de sa vie et il a choisi un certain nombre d'approches différentes. Ces approches sont basées sur différentes hypothèses explicitement énoncées, voire implicites, surtout sur les propriétés des molécules (alors) non directement observables. Déjà dans ses premiers travaux sur la mécanique statistique en 1866, Boltzmann affirmait "fournir une preuve purement analytique et parfaitement générale du second principe de la thermodynamique et trouver le théorème correspondant de la mécanique". Plus tard, Boltzmann s'est éloigné de cette exigence et pensa qu'une telle preuve générale serait impossible.
L'application révolutionnaire de Boltzmann était la méthode statistique. Il est donc, à côté de James Clerk Maxwell et de Josiah Willard Gibbs, fondateur de la mécanique statistique. Maxwell avait déterminé en 1860 la distribution des vitesses dans un gaz en équilibre thermique. Les résultats de Maxwell ont été généralisés par Boltzmann et sont connus aujourd'hui sous le nom de distribution de Maxwell-Boltzmann. Gibbs a réussi à étendre les résultats de Maxwell et Boltzmann, limités aux gaz, à des systèmes arbitraires en introduisant la notion d'ensemble.
Théorème H
À la fin de son article « Études complémentaires » de 1872, page 335, Boltzmann formule le théorème H qu'il écrit ainsi :
Boltzmann en déduit que la valeur de ne peut jamais augmenter. H est réduite à un facteur constant négatif de même valeur absolue que l'entropie S.
Avec le théorème H, Boltzmann parvient à un fondement théorique du second principe.
Entropie et probabilité
Un autre point fort dans le travail de Boltzmann est son célèbre article Sur la relation entre le second principe de la thermodynamique et la théorie des probabilités, en rapport avec l'équilibre thermique, publié en 1877. Dans ce travail, Boltzmann a utilisé des arguments probabilistes et combinatoires pour conclure que la transition vers l'équilibre thermique et donc vers une augmentation de l'entropie correspondait à une transition d'un état moins probable à un état plus probable. "L'état initial sera très peu probable dans la plupart des cas. Le système évoluera toujours de l'état le moins probable jusqu'à l'état le plus probable, c'est-à-dire vers l'équilibre thermique. En appliquant cela au second principe, nous pouvons identifier la quantité généralement appelée entropie avec la probabilité de cet état." Ce résultat est souvent exprimé sous la forme suivante :
est l'entropie, B est la constante de Boltzmann, est la "probabilité thermodynamique" et est le logarithme naturel. Le terme probabilité n'est pas tout à fait correct. C'est plutôt le nombre d'états ou de micro-états, caractérisés par la position et la vitesse de toutes les particules (un état de l'ensemble du système macroscopique, correspondant, dans le cas d'un gaz, à ses variables d'état, telles que la pression, le volume et la température). Boltzmann lui-même n'a jamais écrit cette équation (c'est Max Planck qui l'a formulée), mais elle est implicite dans ses calculs beaucoup plus complexes.
Mécanique et électrodynamique
Boltzmann a considéré la mécanique fondée par Newton, Euler, Lagrange et Hamilton comme le fondement de toute science. Il a également appliqué sa maîtrise de la mécanique à d'autres domaines. Cela est particulièrement vrai pour ses travaux sur l'électrodynamique. La théorie de l'électromagnétisme, développée par James Clerk Maxwell dans les années 1860, rassemblait des disciplines séparées à l’origine (électricité, magnétisme, optique) en une formulation unique. Boltzmann a joué un rôle majeur en faisant connaître les travaux de Maxwell en pays de langue allemande. En 1895, il a traduit en allemand et commenté l'essai de Maxwell intitulé Sur les lignes de force de Faraday.
Acoustique et électricité
Bien que Boltzmann soit surtout connu comme physicien théoricien ou mathématicien, il a également obtenu des résultats importants en physique expérimentale. Malgré sa déficience visuelle sévère, il était considéré comme un expérimentateur qualifié. Au début de son séjour à Graz, il a travaillé avec Toepler dans le domaine de l'acoustique. Il a aussi déterminé la constante diélectrique de différents matériaux en mettant au point ses propres méthodes. Suivant une intuition de Maxwell, il a démontré que l'indice de réfraction d'un matériau est une moyenne géométrique de sa constante diélectrique , que l'on appelle maintenant permittivité, et de sa perméabilité magnétique .
Loi sur le rayonnement du corps noir
En 1879, Josef Stefan avait déterminé expérimentalement que la puissance thermique rayonnée par un corps noir était proportionnelle à la puissance quatrième de sa température. En 1884, Boltzmann publie la justification théorique de la loi de Stefan. En mettant en œuvre les lois de Maxwell, il démontre théoriquement la validité de cette relation qui est désormais appelée loi de Stefan-Boltzmann. Elle établit que l'exitance[10] énergétique d'un corps en watts par mètre carré est liée à sa température exprimée en kelvins selon la relation :
Le coefficient de proportionnalité est connu sous le nom de constante de Stefan-Boltzmann. Le coefficient est l'émissivité (flux radiatif émis par un élément de surface à une température donnée, rapporté à la valeur de référence qu’est le flux émis par un corps noir à cette même température). C'est un coefficient sans unité, compris entre 0 et 1, et qui est l'unité pour un corps noir.
Hendrik Lorentz qualifiera la démonstration de Boltzmann de « perle de la physique théorique ».
Théorie atomique
Au début du XIXe siècle, les chimistes ont été progressivement conduits à envisager la matière comme composée d'éléments distincts associés en proportions simples. Joseph Proust a formulé la loi des proportions définies. John Dalton en a déduit l'existence des atomes comme blocs de construction des composés chimiques. William Prout a remarqué que les poids atomiques sont approximativement des multiples du poids atomique de l'atome d'Hydrogène. Au milieu du XIXe siècle, l'existence des atomes était universellement reconnue par les chimistes. La construction du tableau périodique des éléments par Mendeleiev (1869) a marqué la fondation de la théorie atomique.
- « Notre conception habituelle de la matière, telle qu'elle est présentée par la physique aujourd'hui, nous dit que les matériaux ordinaires à l'échelle macroscopique sont faits d'atomes. Bien que l'essentiel de cette vision des choses remonte au temps des Grecs, son acceptation générale est extrêmement récente. À partir du milieu du XIXe siècle, un nombre croissant de physiciens en sont venus à accepter la réalité des atomes, mais il y en avait encore un grand nombre qui regardaient cette "hypothèse atomique" simplement comme une fiction commode qui ne reflétait en rien la réalité au niveau infra microscopique. »[11]
C'est cette approche à la fois atomique (ou moléculaire) et statistique qui caractérise l'œuvre de Boltzmann. À la suite des chimistes, elle se répandait aussi parmi les physiciens à la fin du XIXe. Cependant, les controverses qui ont émaillé les dix dernières années de Boltzmann ont fait croire que cette façon originale de traiter les problèmes était très peu répandue parmi les physiciens et que Boltzmann avait fait l'objet d'un ostracisme marqué de la part de ses collègues. En réalité, Boltzmann a été sollicité pour enseigner dans de nombreuses universités en Allemagne, y compris à Berlin, et il a été invité et honoré en Grande-Bretagne et aux États-Unis. Contrairement à un mythe répandu (qu'il a entretenu lui-même), il n'a pas été méconnu ni méprisé, ni persécuté par ses collègues. Il se trouve que Boltzmann aimait la polémique et, comme beaucoup de personnes caractérielles, il accusait les autres des controverses qu'il avait déclenchées lui-même[12]. En revenant à Vienne en 1894, il s'est trouvé directement en contact avec Ernst Mach qui proclamait ouvertement ne pas croire à l'existence des atomes... et Boltzmann s'est senti menacé et obligé de se défendre. Il a mis en avant l'utilité des atomes ou des molécules pour expliquer le comportement thermique des gaz. Si Mach défendait le caractère continu de la matière et ne voulait considérer que les choses visibles, Ostwald défendait plutôt l'énergie comme constitutive de l'Univers. Le débat public entre Boltzmann et Ostwald à Lubeck mentionné plus haut avait été minutieusement préparé par Boltzmann qui avait eu communication préalable de la conférence d'Ostwald. C'était un traquenard auquel Ostwald ne s'attendait pas[12]. Ostwald ne lui en a pas tenu rigueur puisqu'il l'a invité à venir enseigner à Leipzig en 1900.
Malheureusement, c'est au moment où ses découvertes triomphent que Boltzmann sombre dans la dépression et meurt. Pourtant, c'est au nom de la théorie moléculaire de la chaleur qu'Einstein a proposé en 1905 que le mouvement des particules observé au microscope par Brown pouvait être provoqué par l'agitation thermique des molécules d'eau [13]. Ce que Jean Perrin a démontré en 1909 :
- « Ainsi, la théorie moléculaire du mouvement brownien peut être regardée comme expérimentalement établie, et, du même coup, il devient assez difficile de nier la réalité objective des molécules. » (p. 61)[4]
Enfin, un des grands arguments des anti-atomistes, la non-visibilité des atomes, s'est trouvé définitivement dévalué en 1912 lorsque Max von Laue a mis en évidence la disposition des atomes dans un cristal en utilisant la diffraction des rayons X.
Philosophie
Au cours de sa carrière de physicien, Boltzmann eut également l'occasion d'adopter un point de vue philosophique plus général sur les sciences. Tout en s'inscrivant pleinement dans la tradition de philosophie des sciences autrichiennes, ses positions peuvent également être considérées tout à la fois comme une anticipation des conceptions de Thomas Kuhn relatives aux révolutions scientifiques. Partisan d'une approche évolutionniste inspirée des travaux de Charles Darwin, Boltzmann considère les théories scientifiques comme autant d' « images du monde » susceptibles d'évoluer en fonction de notre cadre culturel. Il développe également la thèse selon laquelle la connaissance consiste principalement en une élaboration de modèles, et il systématise cette idée dans l'article Modèle qu'il rédige pour l'Encyclopædia Britannica. Ces conceptions exerceront une influence sur le positivisme logique du Cercle de Vienne, ainsi que sur Ludwig Wittgenstein[14].
Publications de Ludwig Boltzmann
Les œuvres de Boltzmann se répartissent en 3 catégories selon les publics visés :
- les articles scientifiques présentant ses travaux de recherche et destinés à ses collègues chercheurs
- les manuels issus de ses cours et destinés aux étudiants
- les articles de vulgarisation publiés dans la presse et destinés au grand public
Publications scientifiques
Les 133 publications scientifiques de Ludwig Boltzmann ont été rassemblées en 3 volumes et publiées après sa mort [15],[16],[17]. Elles sont numérotées par ordre de parution. Les principales publications ont été sélectionnées par Jos Ufkin [18].
- Art-1 Ludwig Boltzmann, « Sur le mouvement de l'électricité sur les surfaces courbes (Über die Bewegung der Elektrizität in krummen Flächen) », Sitzungsberichte der Kaiserlichen Akademie der Wissenschafte, Vol.52/II, , p. 214-221.
- Art-2 Ludwig Boltzmann, « Sur la signification mécanique du second principe de la théorie de la chaleur (Über die Mechanische Bedeutung des Zweiten Hauptsatzes der Wärmetheorie) », Wiener Berichte, Vol.53, , p. 195-220.
- Art-3 Ludwig Boltzmann, « À propos du nombre d'atomes dans les molécules de gaz et de l'énergie interne dans les gaz (Über die Anzahl der Atome in den Gasmolekülen und die innere Arbeit in Gasen) », Wiener Berichte, Vol.56, , p. 682-690.
- Art-5 Ludwig Boltzmann, « Étude sur l'équilibre de la force vive de points matériels en mouvement (Studien über das Gleichgewicht der lebendigen Kraft zwischen bewegten materiellen Punkten) », Wiener Berichte, Vol.58, , p. 517-560.
- Art-18 Ludwig Boltzmann, « À propos de l'équilibre thermique des molécules de gaz polyatomique (Über das Wärmegleichgewicht zwischen mehratomigen Gasmolekülen) », Wiener Berichte, Vol.63, 1871a, p. 397-418.
- Art-19 Ludwig Boltzmann, « Quelques remarques générales sur l'équilibre thermique (Einige allgemeine Sätze über Wärmegleichgewicht) », Wiener Berichte, Vol.63, 1871b, p. 679-711.
- Art-20 Ludwig Boltzmann, « Preuve analytique du second principe de la théorie mécanique de la chaleur à partir des propositions sur l'équilibre de la force vive (Analytischer Beweis des zweiten Haubtsatzes der mechanischen Wärmetheorie aus den Sätzen über das Gleichgewicht der lebendigen Kraft) », Wiener Berichte, Vol.63, 1871c, p. 712-732.
- Art-22 Ludwig Boltzmann, « Études complémentaires sur l'équilibre thermique des molécules de gaz (Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen) », Wiener Berichte, Vol.66, , p. 275-370.
- Art-24 Ludwig Boltzmann, « Détermination expérimentale de la constante diélectrique des isolants (Experimentelle Bestimmung der Dielektrizitätskonstante von Isolatoren) », Wiener Berichte, Vol.67, , p. 17-80.
- Art-26 Ludwig Boltzmann, « Détermination expérimentale de la constante diélectrique de quelques gaz (Experimentelle Bestimmung der Dielektrizitätskonstante einiger Gase) », Wiener Berichte, Vol.69, , p. 794-813.
- Art-39 Ludwig Boltzmann, « Notes sur certains problèmes de la théorie mécanique de la chaleur (Bermerkungen über einige Probleme der mechanische Wärmetheorie) », Wiener Berichte, Vol.75, 1877a, p. 62-100.
- Art-42 Ludwig Boltzmann, « Sur le rapport entre le second principe de la théorie mécanique de la chaleur et la théorie des probabilités en relation avec les lois de l'équilibre thermique (Über die beziehung dem zweiten Haubtsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht) », Wiener Berichte, Vol.76, 1877b, p. 373-435.
- Art-63 Ludwig Boltzmann, « Communication sur l'article de J.C. Maxwell : "Sur le théorème de Boltzmann concernant la distribution moyenne de la force vive dans un système de points matériels" (Referat über die Abhandlung von J.C. Maxwell : “Über Boltzmann's Theorem betreffend die mittlere verteilung der lebendige Kraft in einem System materieller Punkte”) », Wied. Ann. Beiblätter, Vol.5, , p. 403-417.
- Art-72 Ludwig Boltzmann, « Dérivation de la loi de Stefan, concernant la dépendance du rayonnement thermique de la température, à partir de la théorie électromagnétique de la lumière (Ableitung des Stefan’schen Gesetzes, betreffend die Abhängigkeit der Wärmestrahlung von der Temperatur aus der electromagnetischen Lichttheorie) », Annalen der Physik und Chemie, Vol.22, , p. 291-294.
- Art-83 Ludwig Boltzmann, « Nouvelle démonstration de deux lois sur l'équilibre thermique des molécules polyatomiques de gaz (Neuer Beweis zweier Sätze über das Wärmegleichgewicht unter mehratomigen Gasmolekülen) », Wiener Berichte, Vol.95, 1887a, p. 153-164.
- Art-86 Ludwig Boltzmann, « À propos de certaines questions sur la théorie cinétique des gaz (Über einige Fragen der Kinetische Gastheorie) », Wiener Berichte, Vol.96, 1887b, p. 891-918.
- Art-97 Ludwig Boltzmann, « Partie III des études sur l'équilibre de la force vive (III. Teil der Studien über Gleichgewicht der lebendigen Kraft) », Munchen Berichte, Vol.22, , p. 329-358.
- Art-112 Ludwig Boltzmann, « Sur certaines questions de la théorie des gaz (On certain questions in the theory of gases) », Nature, Vol.51, 1895a, p. 413-415.
- Art-114 Ludwig Boltzmann, « Sur le théorème du minimum dans la théorie des gaz (On the minimum theorem in the theory of gases) », Nature, Vol.52, 1895b, p. 221.
- Art-119 Ludwig Boltzmann, « Réponse aux considérations de Mr E. Zermelo sur la théorie de la chaleur (Entgegnung an die wärmetheoretischen Betrachtungen des Hrn. E. Zermelo) », Wied. Ann., Vol.57, , p. 772-784.
- Art-120 Ludwig Boltzmann, « À propos du traité de Mr E. Zermelo sur "l'explication mécanique des événements irréversibles" (Zu Hrn Zermelos Abhandlung “Über die mechanische Erklärung irreversibler Vorgänge) », Wied. Ann., Vol.60, 1897a, p. 392-398.
- Art-123 Ludwig Boltzmann, « À propos de certains de mes traités moins connus sur la théorie des gaz et de leur rapport entre eux (Über einige meiner weniger bekannte Abhandlungen über Gastheorie und deren Verhältnis zu derselben) », Deutschen Naturf. und Ärzte, Braunschweig, Vol.69, 1897b, p. 19-26.
- Art-125 Ludwig Boltzmann, « Sur la question de l'existence objective d'un processus dans la nature inanimée (Über die Frage der objektiven Existenz der Vörgange in der unbelebten Natur) », Wiener Berichte, Vol.106, 1897d, p. 83-108.
- Art-128 Ludwig Boltzmann, « Sur ce qu'on appelle la courbe H (Über die sogenannte H-Kurve) », Math. Ann., Vol.50, , p. 325-332.
Manuels

- (de) Ludwig Boltzmann, Conférences sur la théorie de Maxwell sur l'électricité et la lumière. Vol.I (Vorlesungen über Maxwells Theorie der Elektricität und des Lichtes I. Theil), Leipzig, Johann Ambrosius Barth,
- (de) Ludwig Boltzmann, Conférences sur la théorie de Maxwell sur l'électricité et la lumière. Vol.II (Vorlesungen über Maxwells Theorie der Elektricität und des Lichtes II. Theil), Leipzig, Johann Ambrosius Barth,
- (de) Ludwig Boltzmann, Conférences sur la théorie des gaz. Vol.I (Vorlesungen über Gastheorie I. Theil), Leipzig, Johann Ambrosius Barth,
- (de) Ludwig Boltzmann, Conférences sur la théorie des gaz. Vol.II (Vorlesungen über Gastheorie II. Theil), Leipzig, Johann Ambrosius Barth,
- (de) Ludwig Boltzmann, Conférences sur le principe de la mécanique. Vol.I (Vorlesungen über die Principe der Mechanik. I. Theil), Leipzig, Johann Ambrosius Barth,
- (de) Ludwig Boltzmann, Conférences sur le principe de la mécanique. Vol.II (Vorlesungen über die Principe der Mechanik. II. Theil), Leipzig, Johann Ambrosius Barth,
- (de) Hugo Buchholz, Conférences de Ludwig Boltzmann sur le principe de la mécanique. Vol.III (Ludwig Boltzmanns Vorlesungen über die Prinzipe der Mechanik. III. Theil), Leipzig, Johann Ambrosius Barth,
Écrits populaires
Les articles de vulgarisation et des articles écrits en diverses circonstances ont été regroupés dans un volume intitulé Écrits Populaires[19]. On peut citer :
- (de) Ludwig Boltzmann, « Sur le transport aérien (Über Luftschiffahrt) », Populäre Schriften, , p. 81-91.
- (de) Ludwig Boltzmann, « Josef Stefan », Populäre Schriften, , p. 92-103.
- (de) Ludwig Boltzmann, « Sur le caractère indispensable de l'atomisme dans les sciences de la nature (Über die Unentbehrlichkeit der Atomistik in den Naturwissenschaften) », Populäre Schriften, , p. 141-157.
- (de) Ludwig Boltzmann, « Encore une fois sur la théorie atomique (Nochmals über die Atomistik) », Populäre Schriften, , p. 158-161.
- (de) Ludwig Boltzmann, « En mémoire de Joseph Loschmidt (Zur Erinnerung an Josef Loschmidt) », Populäre Schriften, , p. 228-252.
- (de) Ludwig Boltzmann, « Une conférence inaugurale sur la philosophie naturelle (Ein Antrittsvortrag zur Naturphilosophie) publiée dans Die Zeit le 11 décembre 1905 », Populäre Schriften, , p. 338-344.
- (de) Ludwig Boltzmann, « Sur la mécanique statistique (Über statistische Mechanik) », Populäre Schriften, , p. 345-363.
- (de) Ludwig Boltzmann, « Voyage d'un professeur allemand en Eldorado (Reise eines deutschen Professors ins Eldorado) », Populäre Schriften, , p. 403-435.
Notes et références
Note
Références
- « Ludwig Eduard Boltzmann », sur l'Encyclopædia Britannica (consulté le ).
- (en) Carlo Cercignani, Ludwig Boltzmann, the man who trusted atoms, Oxford, Oxford University Press, , 329 p. (ISBN 978-0-19-850154-1, lire en ligne)
- Eduardo Arroyo Pérez, Boltzmann et l'entropie, Paris, RBA France, , 159 p. (ISBN 978-2-8237-0235-4)
- Jean Perrin, « Mouvement brownien et réalité moléculaire », Annales de Chimie et de Physique sér.8, 18, , p. 5-114
- Jacques Bouveresse, « Ludwig Boltzmann, la science autrichienne et le problème de sa réception à l'étranger », Revue Austriaca n°63, , p. 13-32 (lire en ligne).
- « Ludwig Boltzmann at Clark », sur stp.clarku.edu (consulté le )
- (en) James Maxwell, « Illustrations of the dynamical theory of gases. Part I. On the motions and collisions of perfectly elastic spheres », Philosophical Magazine, 4th series, vol.19, , p. 19-32 (lire en ligne)
- (en) James Maxwell, « Illustrations of the dynamical theory of gases. Part II. On the process of diffusion of two or more kinds of moving particles among one another », Philosophical Magazine, 4th series, vol.20, , p. 21-37 (lire en ligne)
- Carlo Cercignani, Reinhard Illner et Mario Pulvirenti, The Mathematical Theory of Dilute Gases, vol. 106, Springer New York, coll. « Applied Mathematical Sciences », (ISBN 978-1-4612-6425-5 et 9781441985248, DOI 10.1007/978-1-4419-8524-8, lire en ligne)
- Appellation recommandée par la Commission internationale de l'éclairage (anciennement émittance énergétique).
- (en) Roger Penrose, Avant-Propos du livre de Carlo Cercignani, Oxford, Oxford University press,
- (en) « Jos Uffink, Boltzmann's work in statistical analysis », sur plato.stanford.edu, 2004, révisé en 2014 (consulté le )
- (de) Albert Einstein, « A propos du mouvement des particules en suspension dans les liquides au repos, en application de la théorie moléculaire de la chaleur (Uber die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen) », Annalen der Physik, vol.17, , p. 549-560
- Jacques Bouveresse, « Journée du centenaire de la mort de Ludwig Boltzmann », sur Le Collège de France, .
- (de) Ludwig Boltzmann, Wissenschaftliche Abhandlungen, Vol. I (1865-1874), Leipzig, Fritz Hasenöhrl, , 652 p. (lire en ligne)
- (de) Ludwig Boltzmann, Wissenschaftliche Abhandlungen, Vol. II (1875-1881), Leipzig, Fritz Hasenörl, , 596 p. (lire en ligne)
- (de) Ludwig Boltzmann, Wissenschaftliche Abhandlungen, Vol. III (1882-1905), Leipzig, Fritz Hasenörl, , 708 p. (lire en ligne)
- https://plato.stanford.edu/entries/statphys-Boltzmann/
- Ludwig Boltzmann, Populäre Schriften, Leipzig, Johann Ambrosius Barth, (lire en ligne)
Bibliographie
- Blackmore, John : « Boltzmann’s concessions to Mach’s Philosophy of science », in Ludwig Boltzmann – Gesamtausgabe, éd. Roman Sexl et John Blackmore, vol. 8 Ausgewählte Abhandlungen, Braunschweig, F. Vieweg, 1982, 156-190
- Jacques Bouveresse, « La philosophie naturelle de Boltzmann », Philosophia Scientiae, no 3(2), 1998-1999, p. 9-30 (lire en ligne)
- Bouveresse, Jacques : « Hertz, Boltzmann et le problème de la ‘vérité’ des théories », in André Lichnérowicz et Gilbert Gadoffre, La vérité est-elle scientifique ?, Paris, Éditions universitaires, 1991, 119-141
- Broda, Engelbert : « Boltzmann and Darwin », in Ludwig Boltzmann – Gesamtausagabe, éd. Roman Sexl et John Blackmore, vol. 8 Ausgewählte Abhandlungen, Braunschweig, F. Vieweg, 1982, 129-143
- D’Agostino, Salvo : « Boltzmann and Hertz on the Bild-conception of Physical Theory » in History of Science, 28, 1990, p. 380-398
- Wilson, Andrew D. : « Mental Representations and Scientific Knowledge : Boltzmann’s Bild Theory of Knowledge in Historical Context », in Physis, 28, 1991, 770-795
Annexes
Articles connexes
- Physique
- Physiciens
Liens externes
- Jacques Bouveresse, « Colloque Ludwig Boltzmann : Mathématiques, physique et philosophie », sur Le Collège de France,
- [MP3] « Temps et thermodynamique quantique », sur Le Collège de france
- Séminaires Bourbaki, Cédric Villani, « Limites hydrodynamiques de l’équation de Boltzmann », sur http://archive.numdam.org, 53e année, 2000-2001, n°893
- (en) « Boltzmann, Ludwig », sur zbMATH
- Anouk Barberousse, « Ludwig Boltzmann, les théories physiques et les atomes », Images de la Physique, CNRS, (lire en ligne)
- Portrait gravé sur un timbre autrichien de 1981
Bases de données et dictionnaires
- Ressources relatives à la recherche :
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Brockhaus Enzyklopädie
- Deutsche Biographie
- Enciclopedia italiana
- Encyclopædia Britannica
- Encyclopædia Universalis
- Encyclopédie Treccani
- Gran Enciclopèdia Catalana
- Hrvatska Enciklopedija
- Swedish Nationalencyklopedin
- Österreichisches Biographisches Lexikon 1815–1950
- Proleksis enciklopedija
- Store norske leksikon
- Notices d'autorité :
- Fichier d’autorité international virtuel
- International Standard Name Identifier
- CiNii
- Bibliothèque nationale de France (données)
- Système universitaire de documentation
- Bibliothèque du Congrès
- Gemeinsame Normdatei
- Bibliothèque nationale de la Diète
- Bibliothèque nationale d’Espagne
- Bibliothèque royale des Pays-Bas
- Bibliothèque nationale de Pologne
- Bibliothèque nationale de Pologne
- Bibliothèque nationale d’Israël
- Bibliothèque universitaire de Pologne
- Bibliothèque nationale de Catalogne
- Bibliothèque nationale de Suède
- Réseau des bibliothèques de Suisse occidentale
- Bibliothèque nationale d’Australie
- WorldCat
- Portail de la physique
- Portail de l’Empire autrichien
- Portail de la philosophie