Théorème H

Le théorème H — parfois prononcé théorème Êta —[1] est un théorème démontré par Boltzmann en 1872 dans le cadre de la théorie cinétique des gaz[2]^,[3]. Il décrit l'évolution vers l'équilibre thermodynamique d'un gaz satisfaisant à l'équation de Boltzmann et subissant des interactions élastiques. Selon ce théorème, il existe une certaine grandeur $H(t)$ qui varie de façon monotone au cours du temps, pendant que le gaz relaxe vers l'état d'équilibre caractérisé par la loi de Maxwell pour les vitesses des particules du milieu. Cette quantité est l'opposée de l'entropie thermodynamique.

Le théorème H

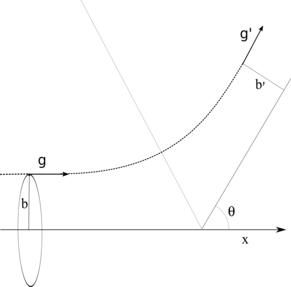
Schéma d'une interaction moléculaire élastique dans le système lié au barycentre.

On peut écrire l'équation de Boltzmann sous la forme suivante[4]^,[5] (équation de Wang Chang et Uhlenbeck)

{\frac {\partial f_{i}}{\partial t}}+\mathbf {v} \cdot \nabla _{x}f_{i}=2\pi \sum _{j}\int _{\mathbf {v} }\int _{0}^{\infty }[f(\mathbf {v} _{i}')f(\mathbf {v} _{j}')-f(\mathbf {v} _{i})f(\mathbf {v} _{j})]\,g_{ij}\,b\,\mathrm {d} b\,\mathrm {d} \mathbf {v} _{j}

où

$f_{i}(\mathbf {x} ,\mathbf {v} ,t)$	distribution des vitesses v au point x et à l'instant t pour la particule i,
$\mathbf {g} _{ij}=\mathbf {v} _{i}-\mathbf {v} _{j}$	vitesse relative avant interaction,
$b$	distance d'impact,

$\mathbf {v} '_{i}$ et $\mathbf {v} '_{j}$ sont les vitesses après interaction.

On introduit la quantité

H=\sum _{i}\int _{\mathbf {v} }f_{i}\log f_{i}\mathrm {d} \mathbf {v} _{i}

En physique statistique cette quantité est l'opposée de l'entropie.

Par dérivation et en tenant compte de l'équation de Boltzmann il vient :

{\frac {\mathrm {d} H}{\mathrm {d} t}}=2\pi \sum _{i}\sum _{j}\int _{\mathbf {v} _{i}}\int _{\mathbf {v} _{j}}\int _{0}^{\infty }(f'_{i}f'_{j}-f_{i}f_{j})(1+\log f_{i})\,g_{ij}\,b\,\mathrm {d} b\,\mathrm {d} \mathbf {v} _{i}\mathrm {d} \mathbf {v} _{j}

Par permutation des indices on peut réécrire cette équation sous la forme suivante :

{\frac {\mathrm {d} H}{\mathrm {d} t}}=-{\frac {\pi }{2}}\sum _{i}\sum _{j}\int _{\mathbf {v} _{i}}\int _{\mathbf {v} _{j}}\int _{0}^{\infty }(f'_{i}f'_{j}-f_{i}f_{j})\log \left({\frac {f'_{i}f'_{j}}{f_{i}f_{j}}}\right)\,g_{ij}\,b\,\mathrm {d} b\,\mathrm {d} \mathbf {v} _{i}\mathrm {d} \mathbf {v} _{j}

Démonstration

L'intégrale peut s'écrire de manière équivalente en intervertissant les indices

{\frac {\mathrm {d} H}{\mathrm {d} t}}=-2\pi \sum _{i}\sum _{j}\int _{\mathbf {v} _{i}}\int _{\mathbf {v} _{j}}\int _{0}^{\infty }(f'_{i}f'_{j}-f_{i}f_{j})(1+\log f'_{i})\,g'_{ij}\,b'\,\mathrm {d} b'\,\mathrm {d} \mathbf {v} '_{i}\mathrm {d} \mathbf {v} '_{j}

Or par réversibilité de l'interaction

g'_{ij}=g_{ij}\,,\qquad b'=b\,,\qquad \mathrm {d} \mathbf {v} '_{i}\mathrm {d} \mathbf {v} '_{j}=\mathrm {d} \mathbf {v} _{i}\mathrm {d} \mathbf {v} _{j}

Donc

{\frac {\mathrm {d} H}{\mathrm {d} t}}=-2\pi \sum _{i}\sum _{j}\int _{\mathbf {v} _{i}}\int _{\mathbf {v} _{j}}\int _{0}^{\infty }(f'_{i}f'_{j}-f_{i}f_{j})(1+\log f'_{i})\,g_{ij}\,b\,\mathrm {d} b\,\mathrm {d} \mathbf {v} _{i}\mathrm {d} \mathbf {v} _{j}

En prenant la demi-somme des deux expressions de la dérivée de H il vient

{\frac {\mathrm {d} H}{\mathrm {d} t}}=-\pi \sum _{i}\sum _{j}\int _{\mathbf {v} _{i}}\int _{\mathbf {v} _{j}}\int _{0}^{\infty }(f'_{i}f'_{j}-f_{i}f_{j})\log \left({\frac {f_{i}}{f'_{i}}}\right)\,g_{ij}\,b\,\mathrm {d} b\,\mathrm {d} \mathbf {v} _{i}\mathrm {d} \mathbf {v} _{j}

On obtient deux nouvelles expressions de la dérivée en intervertissant les indices i et j dans les deux expressions équivalentes ci-dessus. On prend alors le quart de la somme de toutes ces expressions pour obtenir l'équation souhaité.

L'intégrande est de la forme $(x-y)\log \left({\frac {x}{y}}\right)$ :

si x > y alors les deux parties sont positives,
si x < y alors les deux parties sont négatives.

Dans tous les cas ce terme est donc positif ou nul et l'intégrale est elle-même positive ou nulle, donc :

{\frac {\mathrm {d} H}{\mathrm {d} t}}\leq 0

La vitesse à laquelle relaxe le milieu a fait l'objet de nombreuses études centrées autour de la conjecture de Cercignani.

Aspects historiques

La théorie cinétique des gaz, qui est basée sur l'application de la mécanique classique aux molécules constituant le gaz à l'échelle microscopique, s'est développée à partir des travaux fondateurs de James Clerk Maxwell (1850). Par la suite Ludwig Boltzmann (1872 et 1877)[2] puis Willard Gibbs (1902)[6] lui ont donné la forme que l'on trouve dans les ouvrages classiques.

Loschmidt puis Zermelo formulèrent des critiques virulentes contre le théorème H, Boltzmann étant accusé de pratiquer des « mathématiques douteuses ».

Le paradoxe de Loschmidt (1876)

Loschmidt[7]^,[8] se demande comment la grandeur $H(t)$ peut varier de façon monotone au cours du temps alors que la description du système en mécanique classique par l'équation de Liouville est réversible. En effet, si la fonction $H(t)$ était en train de décroître et qu'à un instant donné, on renverse exactement toutes les vitesses de molécules, alors la nouvelle évolution se fait à l'envers, avec $H(t)$ commençant par croître. La réponse de Boltzmann fut brève : « Allez-y, renversez les ! », signifiant l'impossibilité pratique d'une telle opération[N 1].

Avec la découverte du phénomène de sensibilité aux conditions initiales caractéristique des systèmes chaotiques, nous savons aujourd'hui qu'une inversion approchée des vitesses va rapidement entraîner une déviation par rapport à l'orbite initiale exacte inversée, et ce aussi petites que soient les erreurs introduites sur les conditions initiales. Des simulations numériques montrent alors qu'après une inversion approchée, la fonction $H(t)$ commence bien par croître comme le prédisait Loschmidt, mais qu'elle se remet très rapidement à décroître à nouveau et ce pour presque toutes les conditions initiales approchées, l'orbite réelle du système différant de l'orbite initiale exacte inversée.

Le paradoxe de Zermelo (1896)

En 1890, alors qu'il étudie le problème à 3 corps en mécanique céleste, Poincaré démontre un théorème très général : le théorème de récurrence[9]^,[10]. Ce théorème dit que, pour presque toutes les conditions initiales, un système dynamique conservatif dont l'espace des phases est de volume fini[N 2] va repasser au cours du temps aussi près que l'on veut de sa condition initiale, et ce de façon répétée[N 3].

Zermelo[11] fait alors remarquer à Boltzmann en 1896 que le théorème de récurrence de Poincaré semble contredire le fait qu'une grandeur dynamique puisse varier de façon monotone, comme $H(t)$ le fait. La réponse de Boltzmann[12]^,[13] consiste à estimer le temps de récurrence moyen : pour un gaz macroscopique contenant $N\gg 1$ molécules, Boltzmann estime celui-ci d'ordre $10^{N}$ , une durée qui est largement supérieure à l'âge de l'univers[14] lorsque $N\sim {\mathcal {N}}_{A}=6.02\ 10^{+23}$ ; les récurrences sont donc invisibles à notre échelle (voir illustration à Modèle des urnes d'Ehrenfest#Dynamique du modèle.).

Le modèle des urnes d'Ehrenfest (1907)

Le « modèle des urnes » est un modèle stochastique introduit en 1907 par les époux Paul & Tatiana Ehrenfest[15] pour clarifier les paradoxes précédents apparus à la fin du XIX^e siècle dans les fondements de la mécanique statistique[16]. Ce modèle est parfois également appelé le « modèle des chiens & des puces »[17]. Le mathématicien Mark Kac a écrit[18] à son propos qu'il était « probablement l'un des modèles les plus instructifs de toute la physique ».

Ce modèle est exactement soluble ; en particulier, on sait calculer le temps de récurrence moyen de chaque état, ainsi que sa variance pour certains états intéressants.

Le théorème de Lanford (1973)

Lanford a démontré rigoureusement[19]^,[20] qu'un gaz de sphères dures dilué dans $\mathbb {R} ^{3}$ obéit à l'équation de Boltzmann dans la loi d’échelle de Boltzmann-Grad, au moins pour un temps très court, égal seulement à un cinquième du temps de parcours moyen d'un atome[N 4].

En dépit de cette restriction sur la durée, ce théorème mathématique rigoureux est très important conceptuellement, puisque l'équation de Boltzmann entraîne le théorème H. Il est donc aujourd'hui acquis que les mathématiques de Boltzmann ne sont pas « douteuses ».

Voir aussi

Notes

En fait, la théorie des gaz de Boltzmann n'est pas réversible en raison d'une hypothèse dite du « chaos moléculaire » utilisée pour traiter les chocs entre deux molécules. Cette hypothèse énonce qu'avant un choc, les deux vitesses de chaque molécule sont indépendantes, mais corrélées après ce choc. Elle est nécessaire car la description du système se fait par une distribution de vitesses seulement, les positions étant inconnues.
Par exemple, les molécules sont contenues dans un récipient de volume fini, excluant ainsi que les positions deviennent infinies. On supposera également que les vitesses restent toujours finies.
Il existe quelques états exceptionnels pour lequel ceci n'est pas vérifié, mais ces états exceptionnels sont négligeables parmi tous les états possibles, et ce en un sens qui peut être rendu mathématiquement précis.
Temps moyen entre deux collisions consécutives.

Références

(en) Stig Hjalmars, « Evidence for Boltzmann’s H as a capital eta », American Journal of Physics,‎ 1977, p. 214-215 (DOI 10.1119/1.10664, lire en ligne)
(en) Ludwig Boltzmann (trad. de l'allemand), Lectures on Gas Theory, New York, Dover, 1964, 490 p. (ISBN 0-486-68455-5, lire en ligne)
Ludwig Boltzmann, Leçons sur la théorie des gaz, Éditions Jacques Gabay, 1987 (ISBN 978-2-87647-004-0)
(en) Sydney Chapman et Thomas George Cowling, The Mathematical Theory of Non-uniform Gases : an account of the kinetic theory of viscosity, thermal conduction, and diffusion in gases, Cambridge/New York/Port Chester etc., Cambridge University Press, 1991, 422 p. (ISBN 0-521-40844-X)
(en) Joseph Oakland Hirschfelder, Charles Francis Curtiss et Robert Byron Bird, Molecular Theory of Gases and Liquids, John Wiley and Sons, 1966 (ISBN 978-0-471-40065-3)
(en) J. Willard Gibbs, Elementary Principles in Statistical Mechanics, Charles Scribner, 1902 (lire en ligne)
(de) Johann Loschmidt, « Uber das Wärmegleichgewicht eines Systems von Körpern mit Rücksicht auf die Schwere », Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften Wien, Mathematisch-Naturwissenschaftliche Classe, vol. 73,‎ 1876, p. 128-142
(de) Johann Loschmidt, « Uber das Wärmegleichgewicht eines Systems von Körpern mit Rücksicht auf die Schwere », Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften Wien, Mathematisch-Naturwissenschaftliche Classe, vol. 75,‎ 1877, p. 67
Henri Poincaré, « Sur le problème des trois corps et les équations de la dynamique », Acta Mathematica, vol. 13,‎ 1890, p. 1-270
(de) Ludwig Boltzmann, « Uber einen mechanischen Satz von Poincaré », Akademie der Wissenschaften Wien, vol. 106,‎ 1897, p. 12-19 (lire en ligne)
(de) Ernst Zermelo, « Ueber einen Satz der Dynamik und die mechanische Wärmetheorie », Annalen der Physik, vol. 293, n^o 3,‎ 1896, p. 485-494
(de) Ludwig Boltzmann, « Entgegnung auf die wärmetheoretische Betrachtung des Herrn Zermelo », Wied. Ann., vol. 57,‎ 1896, p. 773
(de) Ludwig Boltzmann, « Zu Hrn. Zermelos Abhandlung Uber die mechanische Erkl arung irreversibler Vorg ange », Wied. Ann., vol. 60,‎ 1897, p. 392-398
Environ 14 milliards d'années.
(de) Paul Ehrenfest et Tatiana Ehrenfest, « Ueber zwei bekannte Eingewände gegen das Boltzmannsche H-Theorem », Zeitschrift für Physik, vol. 8,‎ 1907, p. 311-314
(en) Paul Ehrenfest et Tatiana Ehrenfest (trad. de l'allemand), The Conceptual Foundations of the Statistical Approach in Mechanics, New York, Dover, Inc., 1990, 114 p. (ISBN 0-486-66250-0, lire en ligne)
D'après l'anglais : « dog-flea model ».
(en) Mark Kac, Probability and Related Topics in Physical Science, American Mathematical Society, 1957, 266 p. (ISBN 0-8218-0047-7, lire en ligne)
(en) Oscar E Lanford III, Dynamical Systems, Theory and Application, Berlin, Heidelberg, Springer-Verlag, 1975 (ISBN 978-3-540-37505-0), « Time Evolution of Large Classical Systems »
(en) Oscar E Lanford III, Nonequilibrium phenomena I : The Boltzmann equation, North-Holland, 1983, « On a derivation of the Boltzmann equation »

Bibliographie

Cours

Noëlle Pottier, « Physique statistique hors d'équilibre : équation de Boltzmann, réponse linéaire. », sur HAL
Jean Bellissard, « Mécanique Statistique des Systèmes hors d'Équilibre », sur Université Paul Sabatier

Ouvrages

(en) Lev Landau et Evgueni Lifchits, Statistical Physics, Pergamon Press, 1969 (lire en ligne)

Ouvrages

Anouk Barberousse, La mécanique statistique : De Clausius à Gibbs, Paris, Belin, coll. « Collection Histoire des Sciences », 2002, 239 p. (ISBN 2-7011-3073-5)
(en) Carlo Cercignani, Ludwig Boltzmann. The Man who Trusted Atoms, Oxford University Press, 1998 (lire en ligne)
(en) Lawrence Sklar, Physics and Chance : Philosophical Issues in the Foundations of Statistical Mechanics, Cambridge University Press, 1995 (ISBN 0-521-55881-6)

Articles

(en) Jos Uffink, « Boltzmann's Work in Statistical Physics », sur Stanford Encyclopedia of Philosophy, 2004
(en) Jos Uffink, « Compendium of the foundations of classical statistical physics », 2006
(en) Sergio B. Volchan, « Probability as typicality », sur ArXiv
(en) Joël L. Lebowitz, « Macroscopic Laws, Microscopic Dynamics, Time's Arrow and Boltzmann's Entropy' », Physica A, vol. 194,‎ 1993, p. 1-27 (lire en ligne)
(en) Joël L. Lebowitz, « Boltzmann's Entropy and Time's Arrow », Physics Today, vol. 46,‎ 1993, p. 32-38 (lire en ligne)
(en) Joël L. Lebowitz, « Microscopic Reversibility and Macroscopic Behavior: Physical Explanations and Mathematical Derivations », sur ArXiv
(en) Joël L. Lebowitz, « Statistical Mechanics: A Selective Review of Two Central Issues », Reviews of Modern Physics, vol. 71,‎ 1999) (lire en ligne)
(en) Joël L. Lebowitz, « Microscopic Origins of Irreversible Macroscopic Behavior », Physica A, vol. 263,‎ 1999, p. 516-527 (lire en ligne)
(en) Joël L. Lebowitz, « Microscopic Origins of Irreversible Macroscopic Behavior: An overview », sur Université Rutgers
(en) Sheldon Goldstein et Joël L. Lebowitz, « On the (Boltzmann) Entropy of Nonequilibrium Systems », Physica D, vol. 193,‎ 2004, p. 53-66 (lire en ligne)
(en) P. L. Garrido, Sheldon Goldstein et Joel L. Lebowitz, « The Boltzmann Entropy for Dense Fluids Not in Local Equilibrium », Physical Review Letters, vol. 92,‎ 2003 (lire en ligne)
(en) Joël L. Lebowitz, « On the Microscopic Origin of Macroscopic Phenomena », sur Université Rutgers

Portail de la physique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[9] En fait, la théorie des gaz de Boltzmann n'est pas réversible en raison d'une hypothèse dite du « chaos moléculaire » utilisée pour traiter les chocs entre deux molécules. Cette hypothèse énonce qu'avant un choc, les deux vitesses de chaque molécule sont indépendantes, mais corrélées après ce choc. Elle est nécessaire car la description du système se fait par une distribution de vitesses seulement, les positions étant inconnues.

[12] Par exemple, les molécules sont contenues dans un récipient de volume fini, excluant ainsi que les positions deviennent infinies. On supposera également que les vitesses restent toujours finies.

[13] Il existe quelques états exceptionnels pour lequel ceci n'est pas vérifié, mais ces états exceptionnels sont négligeables parmi tous les états possibles, et ce en un sens qui peut être rendu mathématiquement précis.

[24] Temps moyen entre deux collisions consécutives.

[1] (en) Stig Hjalmars, « Evidence for Boltzmann’s H as a capital eta », American Journal of Physics,‎ 1977, p. 214-215 (DOI 10.1119/1.10664, lire en ligne)

[HX7W1I-2] (en) Ludwig Boltzmann (trad. de l'allemand), Lectures on Gas Theory, New York, Dover, 1964, 490 p. (ISBN 0-486-68455-5, lire en ligne)

[3] Ludwig Boltzmann, Leçons sur la théorie des gaz, Éditions Jacques Gabay, 1987 (ISBN 978-2-87647-004-0)

[Chapman-4] (en) Sydney Chapman et Thomas George Cowling, The Mathematical Theory of Non-uniform Gases : an account of the kinetic theory of viscosity, thermal conduction, and diffusion in gases, Cambridge/New York/Port Chester etc., Cambridge University Press, 1991, 422 p. (ISBN 0-521-40844-X)

[Hirschfelder-5] (en) Joseph Oakland Hirschfelder, Charles Francis Curtiss et Robert Byron Bird, Molecular Theory of Gases and Liquids, John Wiley and Sons, 1966 (ISBN 978-0-471-40065-3)

[6] (en) J. Willard Gibbs, Elementary Principles in Statistical Mechanics, Charles Scribner, 1902 (lire en ligne)

[7] (de) Johann Loschmidt, « Uber das Wärmegleichgewicht eines Systems von Körpern mit Rücksicht auf die Schwere », Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften Wien, Mathematisch-Naturwissenschaftliche Classe, vol. 73,‎ 1876, p. 128-142

[8] (de) Johann Loschmidt, « Uber das Wärmegleichgewicht eines Systems von Körpern mit Rücksicht auf die Schwere », Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften Wien, Mathematisch-Naturwissenschaftliche Classe, vol. 75,‎ 1877, p. 67

[10] Henri Poincaré, « Sur le problème des trois corps et les équations de la dynamique », Acta Mathematica, vol. 13,‎ 1890, p. 1-270

[11] (de) Ludwig Boltzmann, « Uber einen mechanischen Satz von Poincaré », Akademie der Wissenschaften Wien, vol. 106,‎ 1897, p. 12-19 (lire en ligne)

[14] (de) Ernst Zermelo, « Ueber einen Satz der Dynamik und die mechanische Wärmetheorie », Annalen der Physik, vol. 293, n^o 3,‎ 1896, p. 485-494

[15] (de) Ludwig Boltzmann, « Entgegnung auf die wärmetheoretische Betrachtung des Herrn Zermelo », Wied. Ann., vol. 57,‎ 1896, p. 773

[16] (de) Ludwig Boltzmann, « Zu Hrn. Zermelos Abhandlung Uber die mechanische Erkl arung irreversibler Vorg ange », Wied. Ann., vol. 60,‎ 1897, p. 392-398

[17] Environ 14 milliards d'années.

[18] (de) Paul Ehrenfest et Tatiana Ehrenfest, « Ueber zwei bekannte Eingewände gegen das Boltzmannsche H-Theorem », Zeitschrift für Physik, vol. 8,‎ 1907, p. 311-314

[19] (en) Paul Ehrenfest et Tatiana Ehrenfest (trad. de l'allemand), The Conceptual Foundations of the Statistical Approach in Mechanics, New York, Dover, Inc., 1990, 114 p. (ISBN 0-486-66250-0, lire en ligne)

[20] D'après l'anglais : « dog-flea model ».

[21] (en) Mark Kac, Probability and Related Topics in Physical Science, American Mathematical Society, 1957, 266 p. (ISBN 0-8218-0047-7, lire en ligne)

[22] (en) Oscar E Lanford III, Dynamical Systems, Theory and Application, Berlin, Heidelberg, Springer-Verlag, 1975 (ISBN 978-3-540-37505-0), « Time Evolution of Large Classical Systems »

[23] (en) Oscar E Lanford III, Nonequilibrium phenomena I : The Boltzmann equation, North-Holland, 1983, « On a derivation of the Boltzmann equation »