Intersection (mathématiques)

Dans la théorie des ensembles, l'intersection est une opération ensembliste qui porte le même nom que son résultat, à savoir l'ensemble des éléments appartenant à la fois aux deux opérandes : l'intersection de deux ensembles A et B est l'ensemble, noté A ∩ B, dit « A inter B », qui contient tous les éléments appartenant à la fois à A et à B, et seulement ceux-là.

L'intersection des ensembles A et B est représentée dans ce diagramme de Venn par la zone violette centrale.

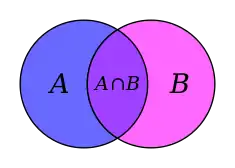
A et B sont disjoints si et seulement si A ∩ B est l'ensemble vide ∅.

A est inclus dans B si et seulement si A ∩ B = A.

En analyse réelle, les points d'intersection des courbes représentatives de deux fonctions interviennent dans la description de leur position relative.

Exemples en géométrie

Intersection de deux droites

Dans le plan

Dans le plan, l'intersection de deux droites non parallèles est un point[1] : $d\cap d'=\{A\}.$ On dit qu'elles sont sécantes.
Si deux droites sont strictement parallèles, elles n'ont pas de point commun ; leur intersection est vide : $d\cap d'=\varnothing .$
Si deux droites sont confondues, tous leurs points sont communs ; l'intersection est une droite : $d\cap d'=d=d'.$

Dans l'espace

Si deux droites ne sont pas coplanaires alors elles n'ont aucun point commun ; leur intersection est vide : $d\cap d'=\varnothing .$
Deux droites parallèles ou sécantes sont coplanaires.

Autres exemples

Dans l'espace

l'intersection d'une droite et d'un plan non parallèles est un point.
l'intersection de deux plans non parallèles est une droite.

Dans le plan

l'intersection d'une droite et d'un cercle est formée de zéro, un ou deux points, selon que la distance du centre du cercle à la droite est supérieure, égale ou inférieure au rayon du cercle. Si l'intersection est réduite à un point, la droite est tangente au cercle.
l'intersection de deux cercles est formée de deux points si la distance entre leurs centres est (strictement) inférieure à la somme de leurs rayons et supérieure à leur différence, d'un point si cette distance est égale à la somme ou à la différence des rayons (cercles tangents), vide dans les autres cas[2].

En géométrie analytique

En géométrie analytique, l'intersection de deux objets est défini par le système d'équations formé par la réunion des équations associées à chaque objet.

En dimension 2, l'intersection de deux droites est définie par un système de deux équations à 2 inconnues, qui a, en général, une solution unique, sauf si son déterminant est nul, auquel cas il en a soit zéro soit une infinité : on retrouve les trois cas de la géométrie.

En dimension 3, l'intersection de trois plans est définie par un système de trois équations à 3 inconnues, qui a, en général, une solution unique, sauf si son déterminant est nul.

En algèbre booléenne

En algèbre booléenne, l'intersection est associée à l'opérateur logique et : si A est l'ensemble des éléments de E possédant la propriété P (ou satisfaisant la condition P) et B l'ensemble des éléments de E possédant la propriété Q (ou satisfaisant la condition Q ), alors A ∩ B est l'ensemble des éléments de E possédant la propriété PetQ (ou satisfaisant à la fois la condition P et la condition Q ).

Exemple 1 : si E est l'ensemble des entiers naturels inférieurs à 10, A l'ensemble des éléments de E impairs, et B l'ensemble des éléments de E premiers, alors A ∩ B est l'ensemble des éléments de E impairs et premiers :

A = {1, 3, 5, 7, 9} , B = {2, 3, 5, 7}, A ∩ B = {3, 5, 7}.

Exemple 2 : l'intersection de l'ensemble des rectangles (quadrilatères ayant leurs quatre angles droits) et de l'ensemble des losanges (quadrilatères ayant leurs quatre côtés égaux) est l'ensemble des carrés (quadrilatères ayant leurs quatre angles droits et leurs quatre côtés égaux).

On définit de même l'intersection d'une classe quelconque d'ensembles (non nécessairement réduite à deux ensembles, ni même finie, ni même indexée par un ensemble : on demande seulement qu'elle soit non vide).

Propriétés algébriques

L'intersection est associative, c'est-à-dire que, pour des ensembles A, B et C quelconques, on a :
(A ∩ B) ∩ C = A ∩ (B ∩ C).
L'intersection est commutative, c'est-à-dire que, pour des ensembles A et B quelconques, on a :
A ∩ B = B ∩ A.
L'union est distributive sur l'intersection, c'est-à-dire que, pour des ensembles A, B et C quelconques, on a :
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).

Intersection d'une famille d'ensembles

On généralise ce concept à une famille d'ensembles (E_i)_i∈I (non nécessairement réduite à deux ensembles, ni même finie). L'intersection des E_i, notée ∩_i∈I E_i, est l'ensemble des éléments communs à tous les E_i (si I est l'ensemble vide, cette intersection n'est donc pas définie dans l'absolu).

Formellement :

\forall x,\quad x\in \bigcap _{i\in I}E_{i}\Leftrightarrow (\forall i\in I,\ x\in E_{i}).

Notes

Pour être rigoureux, on devrait dire ici : « est un singleton » ; l'abus « est un point » est considéré comme acceptable.
Pour le démontrer, il suffit de supposer les cercles, centrés en A et B, sécants en M, et d'écrire les inégalités triangulaires dans le triangle ABM.

Articles connexes

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Pour être rigoureux, on devrait dire ici : « est un singleton » ; l'abus « est un point » est considéré comme acceptable.

[2] Pour le démontrer, il suffit de supposer les cercles, centrés en A et B, sécants en M, et d'écrire les inégalités triangulaires dans le triangle ABM.