Théorème de Siacci
Le théorème de Siacci est un théorème de cinématique qui permet d'exprimer l'accélération d'un point matériel en la projetant sur les directions du vecteur position (direction radiale) et du vecteur vitesse (direction tangentielle) de ce point à un instant donné. Il est important de souligner que ces deux directions ne sont en général pas orthogonales, même pour une trajectoire plane. Il est dû au mathématicien et balisticien Italien Francesco Siacci (1839–1907).
La décomposition de Siacci diffère donc sensiblement de l'expression du vecteur accélération du point selon les directions tangentielle et orthoradiale, donc dans un repère local orthonormé par construction, donnée dans le cas de la décomposition de Serret-Frenet.
L'intérêt du théorème de Siacci est surtout historique, mais il peut être intéressant dans le cas du mouvement à force centrale.
Notions préliminaires : repère de Serret-Frenet
Définitions générales
En cinématique du point, la trajectoire est la courbe géométrique décrite par le lieu des positions successives du point matériel (noté M) au cours du temps t, dans son déplacement par rapport à un référentiel donné. Il s'agit donc d'une courbe paramétrique, qui n'est pas nécessairement plane. Il est cependant toujours possible d'orienter positivement cette courbe selon le sens du mouvement, et de prendre un point quelconque de la trajectoire comme origine.
Dans ce contexte, il est possible de définir l'abscisse curviligne s(t) comme la distance parcourue le long de la trajectoire par le point matériel depuis l'origine sur la trajectoire, à une date t donnée. La distance est bien sûr évaluée selon le sens du mouvement, et donc avec cette convention l'abscisse curviligne est une grandeur positive.
Le vecteur position du point matériel P est le vecteur , O étant un point quelconque de l'espace, donc pas nécessairement situé sur la trajectoire, pris pour origine.
Les vecteurs vitesse et accélération du point matériel P sont alors définis comme les deux dérivées successives par rapport au temps du vecteur position:
- ;
- .
Afin de résoudre les problèmes, il faut exprimer ces grandeurs dans des repères appropriés.
Repère de Frenet
Plutôt que d'exprimer les vecteurs position, vitesse et accélération dans un repère géométrique fixe lié à l'origine O, il est possible d'utiliser un repère mobile, d'origine au point P, défini par:
- le vecteur unitaire tangent , dont la direction est celle de la tangente à la trajectoire au point P et le sens est celui du mouvement;
- le vecteur unitaire orthonormal , dont la direction est celle de la perpendiculaire à la tangente en P dans le plan osculateur à la trajectoire, dirigé selon le centre de courbure;
- le vecteur unitaire binormal , perpendiculaire au plan osculateur donné par , et orienté de telle sorte que les trois vecteur unitaires forment un trièdre direct, il suffit de poser: .
Bien entendu l'expression des vecteurs vitesse et accélération nécessite de dériver les vecteurs de base du trièdre par rapport au temps, et il est qu'alors il vient par exemple . Il est possible de montrer que la dérivation des vecteurs de base par rapport à l'abscisse curviligne peut se mettre sous la forme suivante:
- , où est la courbure de la trajectoire au point P, inverse du rayon de courbure , qui lui correspond au rayon du "cercle tangent instantané" à la trajectoire dans le plan osculateur;
- , où est la torsion de la courbe, qui traduit la tendance du plan osculateur à s'incliner si la trajectoire n'est pas plane (sinon ).
- , bien entendu si la trajectoire est plane cette quantité est nulle et la binormale garde une direction fixe dans d'espace.
Expressions des vecteurs vitesse et accélération
A partir des expressions précédentes il est possible de démontrer que les vecteurs vitesses et accélération se décomposent ainsi dans le repère de Frenet:
- ;
- .
Comme le repère local de Frenet est orthonormal, ces expressions correspondent bien aux composantes des deux vecteurs dans ce repère, et il est facile d'exprimer la valeur de la vitesse et de l'accélération en fonction de celles-ci.
Théorème de Siacci
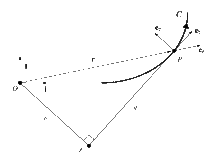
Dans sa publication originale[1] Siacci propose une décomposition du vecteur accélération selon la direction du vecteur position, appelée direction radiale, notée et la direction tangentielle (cf. figure ci-contre).
Enoncé
Dans le cas simple d'une trajectoire contenue à tout moment dans un plan, le théorème de Siacci s'écrit:
- ,
ou encore, en faisant apparaître plutôt le rayon de courbure:
- ,
où p est la distance entre la projection orthogonale de l'origine O sur la direction de la tangente à la trajectoire en P, autrement dit la distance à la podaire par rapport à l'origine O, et , qui correspond au moment cinétique par unité de masse du point matériel par rapport à O[2],[3].
Démonstration
La démonstration du théorème de Siacci est assez facile[4] et consiste à utiliser l'expression du vecteur position dans le trièdre de Serret-Frenet:
- ,
pour introduire le vecteur unitaire de la direction radiale . Il est alors facile d'exprimer le vecteur unitaire normal en fonction de et de , il vient:
- , expression valable pour p ≠ 0.
La substitution dans l'expression de Frenet de l'accélération permet d'obtenir sans difficulté l'expression:
- .
Afin de faire apparaître la quantité h, il convient d'utiliser le fait que [5].
Il vient alors facilement , et finalement l'expression donnée plus haut du théorème de Siacci dans le cas du mouvement plan.
Cas d'une trajectoire non-plane
Le théorème de Siacci peut être généralisé au cas où la trajectoire du point matériel P dans le référentiel d'étude n'est pas plane (courbe gauche)[6].
Dans ce cas l'expression précédente est modifiée en ce qui concerne la composante tangentielle et devient:
- ,
où b est la distance à la date t entre le plan osculateur et l'origine du repère.
En réalité, l'expression établie lors de la démonstration dans le cas d'une courbe plane, sans faire intervenir le moment cinétique par unité de masse h, est toujours valable:
- .
Toutefois, dans le cas d'une trajectoire gauche, l'expression de la dérivée curviligne de h est modifiée car dans ce cas , ce qui conduit après réarrangements à l'expression proposée plus haut du théorème de Siacci.
Applications
Il est important de souligner que le théorème de Siacci donne une décomposition de l'accélération d'un point matériel selon un repère non-orthogonal. Par suite en toute rigueur il est erroné de parler de "composantes" radiale et tangentielle de l'accélération avec cette décomposition.
Le théorème de Siacci peut être utilisé dans le cas d'un champ central de centre O. Dans ce cas la trajectoire est plane et la partie tangentielle de l'accélération sera par hypothèse nulle:
- , par suite , le moment cinétique garde une valeur fixe tout le long de la trajectoire. En fait cela correspond à une vitesse aréolaire constante (loi des aires), puisque que le moment cinétique par unité de masse est dans ce cas proportionnel à cette vitesse.
Par ailleurs en notant f(r) pour la valeur de l'accélération radiale, il vient d'après le théorème de Siacci la relation:
- , or il est possible de montrer[4] que , par suite il vient en intégrant:
- , relation qui correspond en fait à la conservation de l'énergie.
Notes et références
- Siacci F. et 1879 Atti. R. Accad. Sci. Torino, vol.14, p. 750–760
- En effet, il est possible d'écrire pour le vecteur position , la distance q étant le projeté orthogonal du vecteur position sur la tangente à la trajectoire à la date considérée (cf. figure). Il vient alors pour le moment cinétique par rapport à l'origine du point matériel (de masse notée m):
- ,
- Dans ce contexte de la mécanique céleste, il s'agit en fait de la constante des aires généralement notée C: cf. article mouvement képlerien
- Casey et 2011 Meccanica, vol. 46, p. 471-476
- Ceci peut être facilement démontrer replaçant l'expression du vecteur position dans la définition du vecteur unitaire tangent , il vient facilement , il est évident que cette égalité n'est vérifiée que si et .
- Siacci F. et 1879 Atti. R. Accad. Sci. Torino, vol.14, p. 946-951
Bibliographie
- Siacci F., « Moto per una linea piana, », Atti. R. Accad. Sci. Torino, vol. 14, , p. 750–760
- Siacci F., « Moto per una linea gobba, », Atti. R. Accad. Sci. Torino, vol. 14, , p. 946–951
- Casey J., « Siacci's resolution of the acceleration vector for a space curve », Meccanica, vol. 46, , p. 471-476 (DOI 10.1007/s11012-010-9296-x)
- Pourciau, « Newton et les podaires, », Arch. of Hist. sciences, contient 22 références sur ce sujet
- Grossman, The sheer joy of celestial mechanics, Birkhauser, (ISBN 3-7643-3832-6), p. 28-30
- Edmund Taylor Whittaker, A treatise on the analytical dynamics of particles and rigid bodies, Cambridge, Mass., USA, Cambridge University Press, coll. « Cambridge Mathematical Library », (réimpr. 1944, 1989 , 1993), 4e éd. (1re éd. 1904), 456 p., broché (ISBN 978-0-521-35883-5, lire en ligne), chap. I (« Kinematical preliminaries »), p. 21-22
- Pierre-Simon de Laplace, Mécanique céleste, Bachelier, 1798-1825
- John Herivel, Background to Newton's “Principia”, Oxford University Press,
- James T. Cushing, « Kepler's Laws and Universal Gravitation in Newton's Principia », American Journal of physics, no 50, , p. 617-628
Voir aussi
Articles connexes
Liens externes
- Portail de la physique