Apprentissage par renforcement

Classiquement, l'apprentissage par renforcement repose sur un processus de décision markovien (MDP), qui propose un cadre pour le problème d'apprendre à réaliser un but. Un agent apprend et prend des décisions. Il réagit face à un environnement. Un problème peut-être défini comme un processus de décision markovien, lorsqu'il présente les propriétés suivantes[20] :

• un ensemble fini d'états ${\displaystyle {\mathcal {S}}}$ de l'agent dans l'environnement. Un état peut inclure la position d'un agent, sa vitesse, la position d'autres objets ;
• un ensemble fini d'actions ${\displaystyle {\mathcal {A}}}$ que l'agent peut effectuer ; Les actions peuvent être de bas niveau comme faire passer du courant dans un moteur d'un des bras d'un robot. Elles peuvent aussi être de haut niveau comme décider de prendre un petit déjeuner. Elles peuvent aussi être mentales ou calculatoires comme décider de faire attention à un objet et de lancer un traitement d'images sur ce dernier ;
• un ensemble de valeurs scalaires "récompenses" que l'agent peut obtenir. La récompense peut être à chaque étape comme par exemple gagner de l'altitude pour un objet volant, le score dans un jeu vidéo. Elle peut aussi être uniquement donnée qu'à la fin de partie : elle vaut typiquement 1 quand l'agent gagne et 0 quand il perd.

À chaque pas de temps t, l'agent perçoit son état ${\displaystyle S_{t}\in {\mathcal {S}}}$. C'est une variable aléatoire. Il perçoit a priori l'ensemble des actions possibles dans l'état ${\displaystyle S_{t}}$, même si l'on peut supposer pour simplifier que l'ensemble des actions est le même dans tous les états[21]. Il choisit une action ${\displaystyle A_{t}}$ et reçoit de l'environnement un nouvel état ${\displaystyle S_{t+1}}$ et une récompense ${\displaystyle R_{t+1}}$. Ainsi, l'agent évolue dans l'environnement et la séquence des états-actions-récompenses s'appelle une trajectoire, et est définie comme suit :

S₀, A₀, R₁, S₁, A₁, R₂, S₂, A₂, R₃, ...

À partir de ses interactions, un algorithme d'apprentissage par renforcement calcule une politique ${\displaystyle \pi$ :{\mathcal {S}}\rightarrow {\mathcal {A}}} , c'est-à-dire une fonction qui à chaque état préconise une action à exécuter, dont on espère qu'elle maximise les récompenses. La politique peut aussi être probabiliste. Dans ce cas, la politique s'écrit ${\displaystyle \pi$ :{\mathcal {A}}\times {\mathcal {S}}\rightarrow [0,1]} , c'est-à-dire que ${\displaystyle \pi (a,s)=\Pr(a_{t}=a\mid s_{t}=s)}$ est la probabilité que l'agent choisisse d'exécuter a dans l'état s.

Afin de quantifier le bon apprentissage de l'algorithme, on introduit le gain comme étant la somme des récompenses obtenues : ${\displaystyle G=R_{0}+R_{1}+\cdots +R_{T}}$ où T est le temps où on atteint un état terminal dans le processus de décision markovien (MDP). Pour des MDPs sans état terminal, la somme infinie ${\displaystyle G=R_{0}+R_{1}+\cdots }$ n'est peut-être pas bien définie. C'est pourquoi l'on introduit un facteur de dévaluation ${\displaystyle \gamma }$ compris entre 0 et 1. On pose alors ${\displaystyle G=\sum _{t=0}^{\infty }\gamma ^{t}R_{t}}$ qui est convergente et bien définie. Selon la valeur de ${\displaystyle \gamma }$, on prend en compte les récompenses plus ou moins loin dans le futur pour le choix des actions de l'agent. Si ${\displaystyle \gamma }$ = 0, l'agent est myope et ne prend que la récompense immédiate ${\displaystyle R_{0}}$.

Ainsi, la méthode de l'apprentissage par renforcement est particulièrement adaptée aux problèmes nécessitant un compromis entre la quête de récompenses à court terme et celle de récompenses à long terme.

Model-based VS model-free. L'algorithme est basé sur un modèle (model-based) s'il prend le modèle de l'environnement en entrée. Typiquement, l'algorithme prend le processus de décision markovien en entrée. En particulier l'algorithme a accès à la fonction de transition et aux probabilités. L'algorithme a accès à ${\displaystyle p(s',r\mid s,a)}$, la probabilité d'être dans l'état ${\displaystyle s'}$ et d'avoir la récompense ${\displaystyle r}$ depuis l'état ${\displaystyle s}$ en exécutant l'action ${\displaystyle a}$. A contrario, un algorithme est model-free s'il n'utilise pas de modèle en entrée. L'algorithme n'utilise pas les probabilités ${\displaystyle p(s',r\mid s,a)}$ car il ne les connait pas. Par contre bien sûr, un algorithme model-free dispose de structures de données pour les états et les actions.

On-policy VS off-policy. L'algorithme est on-policy (par exemple SARSA) lorsqu'il évalue et améliore la politique, qui est la même que celle utilisée pour prendre des décisions durant l'apprentissage. L'algorithme est off-policy (par exemple Q-learning) si la politique évaluée et améliorée est différente de celle que l'agent utilise pour prendre des décisions lors de l'apprentissage[22]. On distingue alors la politique cible (target policy) qui est la politique apprise, de la politique décisionnelle (behavior policy). Les algorithmes off-policy sont généralement plus lents à converger. Par contre les algorithmes off-policy sont plus généralisables (les algorithmes on-policy sont finalement off-policy où la politique cible et la politique décisionnelle sont les mêmes). Les algorithmes off-policy peuvent être utilisés lorsque les épisodes sont générés par un contrôleur non conventionnel, ou par un expert humain[23].

Bootstrap. Un algorithme évalue les états dans lesquels il est bon d'être. On dit qu'il "bootstrap" s'il évalue les états en utilisant les précédentes évaluations. Au contraire, des algorithmes comme Monte Carlo lancent des simulations jusqu'à atteindre un état final pour évaluer et n'utilisent pas d'évaluations précédentes. L'algorithme Monte Carlo ne "boostrap" pas.

Tabulaire VS approximation. Un algorithme tabulaire stocke dans un tableau les valeurs d'un état en exécutant la politique courante (c'est-à-dire s'il est bon d'être dans un état - car soit il est intrinsèquement bon, soit parce qu'en suivant la politique depuis cet état, la récompense obtenue sera plus importante). Typiquement, on stocke dans un tableau ${\displaystyle V}$ les valeurs ${\displaystyle V(s)}$ pour chaque état. D'autres algorithmes stockent à quel point il est bon de jouer une action a dans un état s via un tableau ${\displaystyle Q}$ qui stocke des valeurs ${\displaystyle Q(s,a)}$. Vu le nombre important d'états (problème appelé malédiction de la dimension), certains algorithmes utilisent une approximation de cette table.

Valued-based VS policy-gradient. Un algorithme valued-based apprend la valeur ${\displaystyle V(s)}$ d'être dans un état s, ou alors Q(s, a) qui est la valeur de jouer l'action a dans l'état s. La politique apprise consiste alors à jouer l'action a qui maximise la valeur. SARSA, Q-learning, TD(0) sont valued-based. Un algorithme policy-gradient manipule directement une politique (représentée avec des paramètres). REINFORCE est policy-gradient.

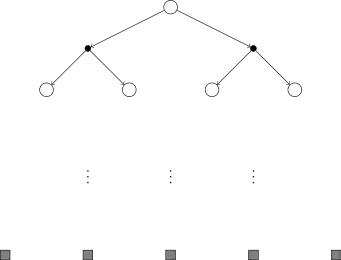
La table suivante donne les quatre grandes classes d'algorithmes[24]. La table donne aussi les diagrammes backup qui sont des diagrammes utilisés dans la littérature et qui résument comment les algorithmes fonctionnent. Dans ces diagrammes, un cercle blanc représente un état ; un point noir représente une action.

L'idée est de calculer une politique a priori optimale par une itération de deux étapes :

1. Évaluation de la politique courante. L'algorithme manipule une table ${\displaystyle V}$ où pour tout état ${\displaystyle s\in {\mathcal {S}}}$, la valeur ${\displaystyle V(s)}$ indique s'il est bon, selon la politique courante, d'être dans l'état ${\displaystyle s}$.
2. Amélioration de la politique courante. Généralement, on utilise une approche gloutonne pour améliorer la politique. Dans chaque état ${\displaystyle s}$, on modifie ${\displaystyle \pi (s)}$ pour choisir l'action qui maximise le gain, selon les valeurs présentes dans la table ${\displaystyle V}$.

L'idée d'itération sur politique générale se trouve dans les approches décrites ci-dessous.

La programmation dynamique est une collection d'algorithmes pour calculer des politiques optimales dans le cas où le MDP est connu[25]. Autrement dit, les comportements de l'environnement sont connus par l'algorithme. Bien que ce cadre ne soit pas réaliste, la programmation dynamique est importante d'un point de vue théorique. On présente ici deux algorithmes : une itération sur politique (qui implémente l'itération sur politique générale présentée plus haut) ; et une itération sur valeur. Selon Sutton et Barto, il est en pratique difficile d'identifier a priori, le meilleur des deux algorithmes[26].

L'itération sur politique consiste à évaluer la valeur ${\displaystyle V}$ de la politique courante ${\displaystyle \pi }$. L'algorithme part d'une politique choisie arbitrairement. Puis successivement : 1. on évalue la politique ; 2. on utilise cette évaluation pour améliorer la politique en cherchant la meilleure action parmi tous les états. Quand la politique n'est plus modifiée, l'algorithme s'arrête.

initialiser arbitrairement ${\displaystyle V(s)}$ et ${\displaystyle \pi (s)}$ pour tout état ${\displaystyle s\in {\mathcal {S}}}$

boucle
     /* 1. évaluer la valeur de la politique */
     boucle
            ${\displaystyle \Delta :=0}$
            pour tout état ${\displaystyle s\in {\mathcal {S}}}$
                    ${\displaystyle v:=V(s)}$
                    ${\displaystyle V(s):=\sum _{s',r}p(s',r\mid s,\pi (s))[r+\gamma V(s')]}$ 
                    ${\displaystyle \Delta :=max(\Delta ,|v-V(s)|)}$
     jusqu'à ce que ${\displaystyle \Delta }$ soit suffisamment petit

     /* 2. amélioration de la politique */
     pour tout ${\displaystyle s\in {\mathcal {S}}}$
             ${\displaystyle \pi (s):=argmax_{a}\sum _{s',r}p(s',r\mid s,\pi (s))[r+\gamma V(s')]}$
     
     si ${\displaystyle \pi }$ n'a pas été modifié dans la boucle pour, alors
                retourner ${\displaystyle V}$, ${\displaystyle \pi }$

L'itération sur valeur est similaire mais combine l'évaluation de la politique et son amélioration.

initialiser arbitrairement ${\displaystyle V(s)}$ et ${\displaystyle \pi (s)}$ pour tout état ${\displaystyle s\in {\mathcal {S}}}$

boucle
     ${\displaystyle \Delta :=0}$
     pour tout état ${\displaystyle s\in {\mathcal {S}}}$
             ${\displaystyle v:=V(s)}$
             ${\displaystyle V(s):=max_{a}\sum _{s',r}p(s',r\mid s,\pi (s))[r+\gamma V(s')]}$   /* ici on fait un max sur toutes les actions */
             ${\displaystyle \Delta :=max(\Delta ,|v-V(s)|)}$
jusqu'à ce que ${\displaystyle \Delta }$ soit suffisamment petit

retourner la politique ${\displaystyle \pi }$ définie par pour tout ${\displaystyle s\in {\mathcal {S}}}$, ${\displaystyle \pi (s):=argmax_{a}\sum _{s',r}p(s',r\mid s,\pi (s))[r+\gamma V(s')]}$

Les méthodes de Monte Carlo diffèrent de l'approche programmation dynamique sur deux aspects[27]. Tout d'abord, avec Monte Carlo, on tire aléatoirement des expériences, et du coup on peut apprendre sans connaître le modèle. Mais aussi elle ne se base pas sur du bootstrap : les valeurs estimées ne sont pas mises à jour en fonction de valeurs estimées précédentes.

Temporal-difference learning (TD) combine les idées de programmation dynamique et Monte Carlo. Tout comme programmation dynamique, il y a du bootstrap dans TD : les valeurs estimées se basent sur les valeurs estimées précédentes. Comme Monte Carlo, TD n'a pas besoin de modèle et peut apprendre directement à partir d'expériences. Par contre, contrairement à Monte Carlo, le bootstrap fait qu'on n'est pas obligé d'atteindre la fin d'un épisode pour commencer à apprendre[28].

L'algorithme prend en entrée une politique ${\displaystyle \pi }$. L'évaluation, c'est-à-dire le calcul de la valeur V se fait directement en interagissant avec l'environnement.

eval(${\displaystyle \pi }$)
       initialiser arbitrairement ${\displaystyle V(s)}$ pour tout état ${\displaystyle s\in {\mathcal {S}}}$
       répéter pour chaque épisode
              initialiser S
               répéter pour chaque pas de temps de l'épisode
                           A := action donnée par ${\displaystyle \pi }$ pour S
                           effectuer l'action a; observer la récompense R et l'état suivant S'
                           ${\displaystyle V(S):=V(S)+\alpha \times [R+\gamma \times (V(S')-V(S))]}$
                           S := S' 
               jusqu'à ce que S soit terminal

Il existe plusieurs algorithmes qui reposent sur le schéma de l'itération sur politique générale. SARSA est on-policy alors que le Q-learning[18] est off-policy.