Planification (intelligence artificielle)
En intelligence artificielle, la planification automatique (automated planning en anglais) ou plus simplement planification, vise à développer des algorithmes pour produire des plans typiquement pour l'exécution par un robot ou tout autre agent. Les logiciels qui incorporent ces algorithmes s'appellent des planificateurs. La difficulté du problème de planification dépend des hypothèses de simplification qu'on tient pour acquises, par exemple un temps atomique, un temps déterministe, une observabilité complète, etc. La compétition IPC (international planning competition) a lieu tous les ans durant le congrès ICAPS (International Conference on Planning and Scheduling)[2].
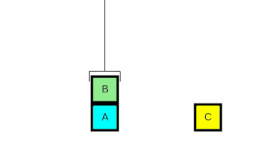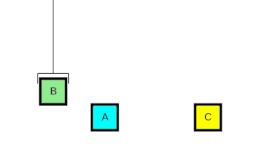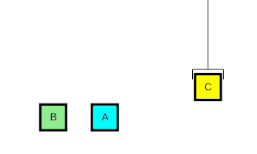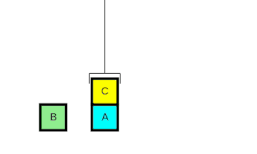
Principe
Un planificateur typique manipule trois entrées décrites dans un langage formel (tel que STRIPS[3] ou PDDL) qui utilise des prédicats logiques :
- une description de l'état initial d'un monde,
- une description d'un but à atteindre et
- un ensemble d'actions possibles (parfois appelés opérateurs).
Chaque action est spécifiée par des préconditions qui doivent être satisfaites dans l'état actuel pour qu'elle puisse être appliquée, et des postconditions (effets sur l'état actuel).
Applications


Un logiciel informatique BRIDGE BARON , utilisant un planificateur, remporte la compétition[4] Baron Barclay World Bridge Computer Challenge, une compétition internationle gérée par le American Contract Bridge League, en . Ce logiciel s'appuyait sur de la planification hiérarchique de tâches.
En 2015, la planification a été utilisée pour construire des programmes qui jouent automatiquement aux jeux Atari[5]. Le système SHPE basé sur de la planification dite hiérarchique permet de faire de la planification pour des jeux vidéo, en particulier des jeux de tir tactique (FPS pour first-person shooter ; ils ont des benchmarks appelés SimpleFPS pour ce type de jeu)[6]. D'autres jeux comme Transformers: Fall of Cybertron[7] ou FEAR[8] utilisent de la planification.
Le téléscope spatial Hubble utilise le planificateur Spike[9], développé par le Space Telescope Science Institute.
Planification classique
La planification classique repose sur deux hypothèses :
- le déterminisme des actions. Par exemple, l'action "poser un cube sur la table" est déterministe. En l'exécutant, on passe d'un état à un autre. Au contraire, "jeter un dé" est non-déterministe car il y a 6 valeurs possibles. L'action "jeter un dé" ne rentre donc pas dans le cadre de la planification classique.
- l'observation parfaite. L'agent (le robot, le programme, etc.) connaît complétement l'état du monde.
En planification classique, il s'agit de chercher une séquence d'actions (par exemple, "prendre une casserole", "mettre de l'eau", "mettre des pâtes", "allumer le feu", "attendre", "éteindre le feu"). L'algorithme A* est un exemple typique d'algorithme de planification classique, souvent employé dans les cours d'introduction pour sa simplicité. Voici quelques techniques algorithmiques utilisées dans les planificateurs classiques :
- la recherche avant dans un espace d'états : algorithme heuristic search planning (HSP)[10], algorithme Fast-Forward (FF)[11],
- la recherche arrière dans un espace d'états,
- la recherche avant dans un espace de plans, Graphplan (en)[12]
- la relaxation d'un problème de planification : on calcule un problème relaxé, pour lequel il est plus simple de savoir s'il existe un plan, qui aide à résoudre le problème initial[13]
- la transformation vers un problème de satisfiabilité d'une formule de la logique propositionnelle.
Bylander a démontré en 1994 que la planification classique est PSPACE-complète[14].
Description formelle
Un problème de planification classique est défini généralement comme un problème de recherche dans un graphe. Chaque état qui décrit l'environnement dans lequel le planificateur cherche un plan est représenté par un nœud dans le graphe et chaque arête entre deux nœuds représente une action qui fait la transition d’un état à un autre.
Formellement un problème de planification classique est défini par une tuple où
- est un ensemble d'états,
- est un ensemble d'actions,
- est une fonction de transition qui à un état et une action associe un état t.q. ,
- est l'état initial,
- est l'ensemble d'états but.
Autres types de planification
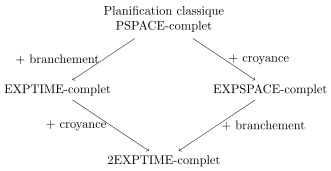
Des extensions généralisent la planification classique, trop restrictives dans certaines applications.
Planification contingente
On parle de planification contingente (contingent planning) où l'environnement est observable grâce à des senseurs, qui peuvent être fautifs. Pour un problème de planification contingente, un plan n'est plus une séquence d'actions mais un arbre de décision car chaque étape du plan est représentée par un ensemble d'états plutôt qu'un seul état parfaitement observable comme dans le cas de la planification classique[16]. Les actions choisies dépendent de l'état du système. Par exemple, s'il pleut, l'agent choisit de prendre le parapluie, et sinon, il peut décider de ne pas le prendre.
Rintanen utilise la terminologie planification conditionnelle (conditionnal planning, comme mentionné par Rintanen dans son article[17] de 2004, p. 1). Mikael L. Littman démontre en 1998 que si on ajoute du branchement (planification contingente), le problème de planification devient EXPTIME-complet[18]. Ce résultat est redémontré par Jussi Rintanen en 2004[17]. Un cas particulier de planification contigente est représentée par les problèmes FOND – pour "fully-observable and non-deterministic". Si le but est spécifié en LTLf (logique temporelle linéaire sur trace finie) alors le problème est toujours EXPTIME-complet[19] et 2EXPTIME-complet pour une spécification du but en LDLf.
Planification conformante
On parle de planification conformante (conformant planning, comme mentionné par Rintanen dans son article[17] de 2004, p. 1) où l'agent est incertain de l'état du système, et que l'agent ne peut faire aucune observation. L'agent a alors des croyances sur le monde réel. Ces problèmes sont résolus par des techniques semblables à celles de la planification classique, mais où l'espace des états est exponentiel dans les dimensions du problème, à cause de l'incertain sur l'état actuel. Une solution pour un problème de conformant planning est une séquence d'actions. Haslum et Jonsson ont démontré que le problème de planification conformante est EXPSPACE-complet[20].
Rintanen a démontré que, si on ajoute à la fois du branchement et de l'incertain (planification à la fois conformante et contingente), le problème devient 2EXPTIME-complet[15]. Dans ce problème, les agents ont une information partielle sur l'état du système mais peuvent disposer de certaines actions d'observation de l'état - par exemple, vérifier s'il pleut ou pas - et ainsi gagner de l'information sur l'état du système.
Planification probabiliste
Kushmerick et al. ont introduit la planification probabiliste[21]. Dans leurs travaux, l'effet des actions est décrite avec des probabilistes. Il donne l'exemple de l'action `le robot prend un bloc' décrite de la manière suivante : si la pince du robot est sèche, alors le robot tient le bloc avec une probabilité 0.95 ; si la pince est humide, alors le robot ne tient le bloc qu'avec une probabilité de 0.5.
Cette problématique est du ressort de la théorie de la décision dans l'incertain. Ceci mène au problème de la génération de politique (ou stratégie) dans un arbre de décision ou dans un diagrame d'influence. Si l'hypothèse Markovienne est posée alors on se place dans le cadre d'un Processus de décision markovien (MDP) ou (dans le cas général) un Processus de décision markovien partiellement observable (POMDP).
Planification non linéaire
La planification classique résout les sous-buts dans un ordre donné. Le problème est que cela amène parfois à détruire ce qui a déjà été construit. Ce phénomène est connu sous le nom d'anomalie de Sussman.
Supposons qu'un individu pieds nus doive se retrouver dans l'état où il porte sa chaussure droite, sa chaussure gauche, sa chaussette droite et sa chaussette gauche. S'il cherche à réaliser les buts dans l'ordre de l'énoncé, il échouera.
Pour résoudre ce type de problème, on peut passer à des plans partiellement ordonnés dans lesquels l'ordre entre les actions n'est fixé que lorsque c'est nécessaire (engagement au plus tard ou least commitment planning).
Dans l'exemple précédent, mettre la chaussure gauche doit se faire après avoir mis la chaussette gauche. Idem pour la droite. En revanche l'exécution du plan pour la gauche est indépendante de l'exécution pour la droite. Le plan global est donc partiellement ordonné.
Les planificateurs capables de gérer cette catégorie de problème sont dits à ordre partiel (POP, NOAH, etc).
Planification hiérarchique
Généralement, lorsque l'on planifie, on peut disposer d'une information hiérarchique sur les actions, c'est-à-dire une description sur comment des actions complexes se décomposent. Par exemple, une action complexe comme "servir un café" peut se décomposer en la séquence de deux actions complexes "préparer un café" puis "apporter le café". Ainsi, il existe des planificateurs, comme ABSTRIPS, qui en plus de la description des actions, prennent en entrée la description hiérarchique des actions. On peut par exemple commencer à planifier à haut niveau puis descendre dans le détail au besoin (comme le fait ABSTRIPS par exemple). L'objectif est alors décrit à l'aide d'un réseau hiérarchique de tâches (HTN pour hierarchical task network en anglais)[22].
Planification temporelle
La planification temporelle permet d'exprimer des durées d'actions, des conditions au début, à la fin et pendant l'action et des effets au début et à la fin des actions. Le langage PDDL 2.1 inclut la planification temporelle[23]. La méthode TLP-GP 1[24] construit un graphe, puis on résout des contraintes temporelles en utilisant un solveur SMT. On backtracke en cas d'inconsistance. Rintanen a démontré que la planification temporelle concurrente (plusieurs instances d'une même action en parallèle est possible) est EXPSPACE-complète. Par contre, si on relâche ces conditions, on peut se ramener à de la planification classique et donc la planification temporelle avec ces restrictions devient PSPACE-complète[25].
Planification générale
La planification générale consiste à produire un plan qui fonctionne pour plusieurs environnements de départ[26].
Planification multi-agents
La planification multi-agents étudie la réalisation d'une tâche par plusieurs agents, par exemple plusieurs robots. La génération du plan et son exécution est alors souvent distribuée/décentralisée[27],[28],[29]. Un aspect important dans les plans est la coopération entre agents. Il existe aussi un algorithme de planification centralisé, qui s'appuie sur une généralisation de STRIPS au cadre multi-agents, appelée MA-STRIPS[30]. L'algorithme a ensuite été rendu distribué, en utilisant un solveur CSP distribué pour gérer la coordination entre agents[31]. Les auteurs, Nissim, Brafman et Domshlak, ont expérimentalement vérifié que leur algorithme est meilleur qu'une planification centralisée lorsque les agents ont peu d'interactions entre eux.
Une difficulté majeure de la planification multi-agent est l'explosion combinatoire de l'ensemble des actions, qui est exponentiel en le nombre d'agents. En 2011, Jonsson et Rovatsos propose une solution pour contrecarrer ce problème et se ramène à de la planification classique mono-agent[32]. Il y a aussi un gain à utiliser des techniques de parallélisation pour que les algorithmes de planification passent à l'échelle[33].
Planification épistémique
Le problème de planification épistémique consiste à prendre en compte les connaissances des agents dans la description des états et des actions[34]. Typiquement, l'objectif est une formule de la logique modale épistémique, comme "l'agent a sait que l'agent b que le bloc C est sur le bloc A" et les actions sont représentées avec des modèles d'actions de la logique épistémique dynamique[34]. Le problème de planification est indécidable dans toute sa généralité[35].
Voir aussi
Bibliographie
- Algorithmique de la planification en IA, Pierre Régnier, Editions Cépaduès, (ISBN 2-85428-658-8)
- (en) Malik Ghallab, Dana Nau et Paolo Traverso, Automated planning, Morgan Kaufmann, (ISBN 1-55860-856-7)
- (en) Michael R. Genesereth and Nils J. Nilsson, Logical Foundations of Artificial Intelligence, Morgan Kaufmann, [détail de l’édition], chap. 12 Planning, pp. 285-306
Articles connexes
Références
- « Projet svganimedit sur gitlab qui contient le code source de l'animation. », sur GitLab (consulté le )
- (en) « IPC2018 »
- Richard E. Fikes et Nils J. Nilsson, « STRIPS: a new approach to the application of theorem proving to problem solving », IJCAI'71 Proceedings of the 2nd international joint conference on Artificial intelligence, Morgan Kaufmann Publishers Inc., , p. 608–620 (lire en ligne, consulté le )
- (en) Tom Throop, Dana Nau et Stephen J. Smith, « Computer Bridge: A Big Win for AI Planning », AI Magazine, vol. 19, no 2, , p. 93–93 (ISSN 2371-9621, DOI 10.1609/aimag.v19i2.1371, lire en ligne, consulté le )
- Nir Lipovetzky, Miquel Ramirez et Hector Geffner, « Classical planning with simulators: results on the Atari video games », IJCAI'15 Proceedings of the 24th International Conference on Artificial Intelligence, AAAI Press, , p. 1610–1616 (ISBN 9781577357384, lire en ligne, consulté le )
- (en) « Cybertron Intel – HTN Planning in Transformers: Fall of Cybertron », AI and Games, (lire en ligne, consulté le )
- (en-US) « Facing Your F.E.A.R », AI and Games, (lire en ligne, consulté le )
- (en) « Spike Planning and Scheduling System »
- (en) « Planning as heuristic search », Artificial Intelligence, vol. 129, nos 1-2, , p. 5–33 (ISSN 0004-3702, DOI 10.1016/S0004-3702(01)00108-4, lire en ligne, consulté le )
- Jörg Hoffmann et Bernhard Nebel, « The FF planning system: fast plan generation through heuristic search », Journal of Artificial Intelligence Research, vol. 14, no 1, , p. 253–302 (ISSN 1076-9757, lire en ligne, consulté le )
- (en) « Fast planning through planning graph analysis », Artificial Intelligence, vol. 90, nos 1-2, , p. 281–300 (ISSN 0004-3702, DOI 10.1016/S0004-3702(96)00047-1, lire en ligne, consulté le )
- Martin Cooper, Frédéric Maris et Pierre Régnier, « Relaxation of Temporal Planning Problems », TIME '13 Proceedings of the 2013 20th International Symposium on Temporal Representation and Reasoning, IEEE Computer Society, , p. 37–44 (ISBN 9781479922413, DOI 10.1109/TIME.2013.28, lire en ligne, consulté le )
- (en) « The computational complexity of propositional STRIPS planning », Artificial Intelligence, vol. 69, nos 1-2, , p. 165–204 (ISSN 0004-3702, DOI 10.1016/0004-3702(94)90081-7, lire en ligne, consulté le )
- (en) Jussi Rintanen, « Complexity of Planning with Partial Observability », ICALP, (lire en ligne)
- (en) Alexandre Albore, Hector Palacios et Hector Geffner, A Translation-Based Approach to Contingent Planning, Pasadena, Californie, AAAI - International Joint Conference of Artificial Intelligence (IJCAI), (lire en ligne).
- (en) Jussi Rintanen, Complexity of Planning with Partial Observability, AAAI, (lire en ligne).
- Michael L. Littman, « Probabilistic Propositional Planning: Representations and Complexity », In Proceedings of the Fourteenth National Conference on Artificial Intelligence, MIT Press, , p. 748–754 (lire en ligne, consulté le )
- Giuseppe De Giacomo et Sasha Rubin, « Automata-Theoretic Foundations of FOND Planning for LTLf and LDLf Goals », IJCAI, (lire en ligne, consulté le )
- (en) Patrik Haslum et Peter Jonsson, « Some Results on the Complexity of Planning with Incomplete Information », Recent Advances in AI Planning, Springer Berlin Heidelberg, lecture Notes in Computer Science, , p. 308–318 (ISBN 9783540446576, DOI 10.1007/10720246_24, lire en ligne, consulté le )
- (en) « An algorithm for probabilistic planning », Artificial Intelligence, vol. 76, nos 1-2, , p. 239–286 (ISSN 0004-3702, DOI 10.1016/0004-3702(94)00087-H, lire en ligne, consulté le )
- Ilche Georgievski et Marco Aiello, « An Overview of Hierarchical Task Network Planning », arXiv:1403.7426 [cs], (lire en ligne, consulté le )
- « Compilation d’un langage de planification temporelle de haut niveau en PDDL2.1 »
- (en-US) « TLP-GP: Solving Temporally-Expressive Planning Problems - IEEE Conference Publication », sur ieeexplore.ieee.org (consulté le )
- Jussi Rintanen, « Complexity of concurrent temporal planning », ICAPS'07 Proceedings of the Seventeenth International Conference on International Conference on Automated Planning and Scheduling, AAAI Press, , p. 280–287 (ISBN 9781577353447, lire en ligne, consulté le )
- (en) Yuxiao Hu et Giuseppe De Giacomo, « Generalized Planning: Synthesizing Plans that Work for Multiple Environments », IJCAI, (lire en ligne, consulté le )
- (en) Edmund H. Durfee, Multi-Agent Systems and Applications, Springer Berlin Heidelberg, (ISBN 978-3-540-42312-6 et 9783540477457, DOI 10.1007/3-540-47745-4_6, lire en ligne), p. 118–149
- (en) Marie E. desJardins, Edmund H. Durfee, Jr Charles L. Ortiz et Michael J. Wolverton, « A Survey of Research in Distributed, Continual Planning », AI Magazine, vol. 20, no 4, , p. 13 (ISSN 0738-4602, DOI 10.1609/aimag.v20i4.1475, lire en ligne, consulté le )
- (en) M. Tambe, « Towards Flexible Teamwork », Journal of Artificial Intelligence Research, vol. 7, , p. 83–124 (ISSN 1076-9757, DOI 10.1613/jair.433, lire en ligne, consulté le )
- Ronen I. Brafman et Carmel Domshlak, « From one to many: planning for loosely coupled multi-agent systems », ICAPS'08 Proceedings of the Eighteenth International Conference on International Conference on Automated Planning and Scheduling, AAAI Press, , p. 28–35 (ISBN 9781577353867, lire en ligne, consulté le )
- Raz Nissim, Ronen I. Brafman et Carmel Domshlak, « A general, fully distributed multi-agent planning algorithm », AAMAS '10 Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems, International Foundation for Autonomous Agents and Multiagent Systems, vol. 1, , p. 1323–1330 (ISBN 9780982657119, lire en ligne, consulté le )
- Anders Jonsson et Michael Rovatsos, « Scaling up multiagent planning: a best-response approach », ICAPS'11 Proceedings of the Twenty-First International Conference on International Conference on Automated Planning and Scheduling, AAAI Press, , p. 114–121 (lire en ligne, consulté le )
- Akihiro Kishimoto, Alex Fukunaga et Adi Botea, « Scalable, parallel best-first search for optimal sequential planning », ICAPS'09 International Conference on International Conference on Automated Planning and Scheduling, AAAI Press, , p. 201–208 (ISBN 9781577354062, lire en ligne, consulté le )
- Thomas Bolander, « A Gentle Introduction to Epistemic Planning: The DEL Approach », Electronic Proceedings in Theoretical Computer Science, vol. 243, , p. 1–22 (ISSN 2075-2180, DOI 10.4204/EPTCS.243.1, lire en ligne, consulté le )
- (en) Thomas Bolander et Mikkel Birkegaard Andersen, « Epistemic planning for single- and multi-agent systems », Journal of Applied Non-Classical Logics, vol. 21, no 1, , Pages 9-34 (lire en ligne)
- Portail de l'informatique théorique