Arbre réel
En mathématiques, un arbre réel, ou arbre continu ou -arbre, est un espace métrique particulier possédant une propriété d'arbre : il existe un « chemin » entre chaque couple de points de l'espace métrique, de plus ce « chemin » est unique pour un couple de points donné.
Pour les articles homonymes, voir Arbre (homonymie).
Intuitivement, un arbre réel peut être vu comme un arbre discret composé de nœuds et d'arêtes à longueur variable. Toutefois, tout point intérieur d'une arête est considéré comme un nœud de l'arbre (de degré 2). L'ensemble des points de branchement (nœuds de degré au moins 3) peut être dense dans l'arbre, ce qui en fait un objet fractal.
Plusieurs définitions équivalentes existent, on peut également « construire » certains arbres réels comme les objets limites de suites d'arbres discrets en faisant tendre leurs longueurs d'arête vers 0.
L'arbre brownien (ou CRT brownien) est un exemple important d'arbre continu en probabilités. C'est un objet fractal dont les arêtes sont de longueur infinitésimale et dont les nœuds sont denses dans l'arbre. En théorie géométrique des groupes, il existe une théorie des actions de groupe sur les -arbres.
Définitions formelles
Un arbre réel est un espace métrique tel que pour tout couple de points , il existe un unique chemin dans dont les extrémités sont et .
Plus formellement, pour tout couple de points , il existe une unique isométrie telle que , et tout chemin injectif de X partant de x et finissant en y est l'image de : .
Ce chemin, que l'on peut noter , est l'unique géodésique de à . On dit que c'est un espace métrique géodésiquement linéaire. On ne traitera ici que du cas où l'espace est compact.
Soit un point de . Le degré de , noté , est le nombre de parties disjointes (deux à deux) de l'ensemble . Si , alors est une extrémité de (feuille ou racine) ; si , alors est un point du squelette de ; si , alors est un point de branchement[1] de .
Si on distingue un point, notons-le , de , l'espace métrique est alors appelé espace métrique pointé. Pour un vocabulaire plus proche des arbres, on dit que l'arbre est enraciné (en la racine ).
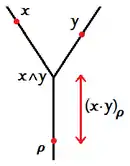
Il est alors possible de définir une relation généalogique. L'ancêtre commun le plus récent de deux points et de est l'unique point tel que . Utilisons la notation . La distance de la racine à est donnée par[2] :
L'espace des arbres réels est un sous-espace de l'espace des espaces métriques. L'espace , muni de la distance de Gromov-Hausdorff, est un espace polonais[2] (métrique, séparable, complet). On peut alors comparer les arbres réels en donnant une distance entre eux et ainsi construire une convergence.
Caractérisations
Voici plusieurs caractérisations équivalentes d'un arbre réel qui peuvent être considérées comme des définitions.
- (similaire aux arbres en tant que graphes) Un arbre réel est un espace métrique connexe qui ne contient pas de sous-ensemble homéomorphe à un cercle[1].
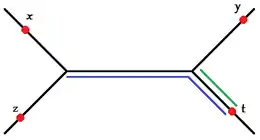
- Un arbre réel est un espace métrique connexe qui vérifie la condition des quatre points[3] (voir figure ci-contre) :
pour tous . - Un arbre réel est isomorphe à un espace métrique connexe 0-hyperbolique[2](voir figure ci-contre). C'est-à-dire,
pour tous . - (similaire à la caractérisation des arbres de Galton-Watson par le processus de contour) Considérons une excursion positive d'une fonction continue . C'est-à-dire, une fonction telle que, , pour tout où est la fin de l'excursion et pour tout . Pour , , on définit une semi-distance et une relation d'équivalence par :
Ainsi, l'espace métrique quotienté est un arbre réel[2].
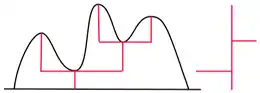
Intuitivement, les minima locaux de l'excursion e sont les pères des maxima locaux. Une autre manière visuelle de construire l'arbre réel à partir d'une excursion est d'appliquer de la colle sous la courbe de e et de « plier » cette courbe, ainsi les points d'une même classe d'équivalence sont identifiés (voir animation ci-dessous).
Exemples
Arbre réel aléatoire
Un arbre réel aléatoire est une variable aléatoire sur l'espace des arbres réel.
Il peut être également défini, grâce à la caractérisation no 4 ci-dessus, en utilisant l'excursion d'un processus stochastique.
Arbre réel binaire
Un arbre réel binaire est un arbre réel dont les nœuds sont de degré 1 (pour les feuilles et la racine), de degré 2 (pour les points de squelette) ou degré 3 (pour les points de branchement binaires).
Les arbres binaires (discrets) en sont un exemple particulier ou chaque arête est de longueur 1.
Arbre brownien
L'arbre brownien ou CRT brownien (CRT sont les initiales de continuum random tree en anglais[4]) est un arbre réel binaire aléatoire engendré par un mouvement brownien. Plus précisément, l'arbre brownien est l'arbre réel défini à partir d'une excursion brownienne et en utilisant la caractérisation 4 (voir ci-dessus).
- Construction par la séparation poissonienne d'une droite
Une des premières construction de l'arbre brownien a été donnée par Aldous[4] en 1991, en utilisant la séparation poissonienne d'une droite (Poisson line-breacking en anglais). On considère un processus de Poisson non homogène N d'intensité r(t)=t (c'est-à-dire que est une variable de Poisson de paramètre ) et les points générés par ce processus de Poisson. On sépare la droite réelle suivant les intervalles . Le segment est l'arbre de départ, on attache le segment suivant en un point choisi uniformément sur l'arbre en cours ; on itère cette opération pour la suite de points . La fermeture de l'objet limite est l'arbre brownien[4].
- Construction comme limite d'arbres de Galton-Watson
Rappelons que l'arbre brownien peut être défini à partir d'une excursion brownienne en utilisant la caractérisation no 4 (voir ci-dessus). De même un arbre de Galton-Watson, ou une forêt de Galton-Waltson, peut être définie à partir d'une excursion (discrète) d'une marche de Łukasiewicz.
Un théorème de convergence de type Donsker permet d'obtenir la convergence des excursions discrètes vers les excursions continues et ainsi permet de définir l'arbre brownien comme limite d'échelle d'arbres de Galton-Watson.
Une autre manière de voir cette convergence est d'utiliser la définition de l'arbre brownien comme espace métrique géodésiquement linéaire. En normalisant convenablement la distance de cet espace métrique, on obtient une limite de l'espace métrique discret vers le CRT brownien. Cette convergence est la convergence de Gromov-Hausdorff dans l'espace des espaces métriques muni de la distance de Gromov-Hausdorff.
Notes et références
- Ian Chiswell, Introduction to Lambda-trees, World Scientific Publishing, 2001, (ISBN 981-02-4386-3)
- Steven N. Evans, Probability and Real Trees, École d’Eté de Probabilités de Saint-Flour XXXV, 2005.
- Peter Buneman, A Note on the Metric Properties of Trees, Journal of combinatorial theory, B (17), p. 48-50, 1974.
- David Aldous, The continuum random tree. I, The annals of probability, Vol. 19, (1), p. 1-28, 1991.
Annexes
Liens internes
Bibliographie
(en) Charles Semple et Mike Steel (en), Phylogenetics, OUP, , 239 p. (ISBN 978-0-19-850942-4, présentation en ligne)
- Portail des mathématiques
- Portail des probabilités et de la statistique