Automate fini non déterministe
Un automate fini (on dit parfois, par une traduction littérale de l'anglais, machine à états finis, au lieu de machine avec un nombre fini d'états ou machine à états finie ou machine finie à états), finite-state automaton ou finite-state machine (FSA, FSM), est une machine abstraite qui est un outil fondamental en mathématiques discrètes et en informatique. On les retrouve dans la modélisation de processus, le contrôle, les protocoles de communication, la vérification de programmes, la théorie de la calculabilité, dans l'étude des langages formels et en compilation. Ils sont utilisés dans la recherche des motifs dans un texte.
Cet article concerne les automates finis. Pour une introduction informelle, voir Automate fini. Pour une présentation générale, voir Théorie des automates.
Pour les automates déterministes, voir Automate fini déterministe. Pour les autres significations, voir Automate.

On distingue les automates finis non déterministes (abrégés en AFN) en anglais non-deterministic finite automaton ou NFA, des automates finis déterministes (abrégés en AFD) en anglais deterministic finite automata ou DFA. Sans précision supplémentaire, un automate fini est toujours non déterministe, mais on devrait plutôt dire « indéterministe », puisqu'il est indifférent qu'il soit déterministe ou non.
Les automates finis (déterministes ou non) reconnaissent exactement des langages rationnels. Ce sont les machines les plus simples dans la hiérarchie de Chomsky, et par conséquent ils sont moins puissants que les automates à pile et, bien entendu, que les machines de Turing.
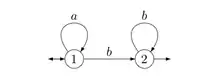
Un automate est constitué d'états et de transitions. Son comportement est dirigé par un mot fourni en entrée : l'automate passe d'état en état, suivant les transitions, à la lecture de chaque lettre de l'entrée. Dans l'exemple ci-dessus, pour l'entrée , et si l'automate démarre en , il passe successivement par les états , le calcul correspondant est :
.
|
|
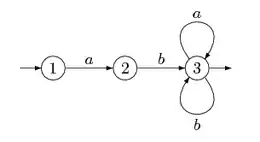
L'automate est dit « fini » car il possède un nombre fini d'états : il ne dispose donc que d'une mémoire bornée. On peut très bien considérer des automates sans limitation sur le nombre d'états : la théorie qui en résulte est très analogue à la théorie habituelle. Un automate fini peut être vu comme un graphe orienté étiqueté : les états sont les sommets et les transitions sont les arêtes étiquetées. L'état initial est marqué par une flèche entrante ; un état final est, selon les auteurs, soit doublement cerclé (dans la figure 1 ci-dessus, l'état est à la fois initial et final), soit marqué d'une flèche sortante (dans la figure 2 ci-dessous, 1 est initial et 3 est final).
Une autre façon commode de représenter un automate fini est sa table de transition. Elle donne, pour chaque état et chaque lettre, l'état d'arrivée de la transition. Voici à droite la table de transition de l'automate de la figure 1 :
Aperçu
Il existe plusieurs types d'automates finis. Les « accepteurs » ou « reconnaisseurs » produisent en sortie une réponse « oui » ou « non », selon qu'ils acceptent (oui) ou rejettent (non) le mot présenté en entrée. Dans l'exemple ci-dessus (Fig. 1), le mot n'est pas accepté, mais le mot est accepté. D'autres automates classent l'entrée par catégorie : au lieu de répondre par oui ou par non, ils répondent par une classification ; de tels automates se rencontrent par exemple en linguistique. Les automates pondérés (weighted automata[1] en anglais) associent à chaque mot une valeur numérique.
Les automates finis servent à caractériser des langages (c'est-à-dire, des ensembles, finis ou non, de mots finis en général) : ce sont les langages composés des mots acceptés, ou langages reconnus par les automates. Des extensions des automates finis reconnaissent des langages de mots infinis. Ce sont les automates sur les mots infinis (les plus connus d'entre eux sont les automates de Büchi), les automates de Rabin et les automates de Muller. D'autres automates reconnaissent divers types d'arbres (automates d'arbres).
Une sous-catégorie importante est celle des automates déterministes (les automates généraux sont parfois appelés non déterministes ; il conviendrait mieux de les qualifier d'« indéterministes »). Un automate est déterministe si, pour chacun de ses états, il y a au plus une transition pour chaque étiquette possible et si, de plus, il a un seul état initial. S'il a exactement une transition par étiquette, on parle alors d'automate déterministe complet. L'automate ci-dessus est déterministe et complet.
Dans les automates non déterministes, il peut y avoir plusieurs transitions à partir d'un état donné pour une étiquette donnée. Ici, le terme « non déterministe » ne signifie pas la négation de « déterministe » (c'est-à-dire « nécessairement non déterministe ») mais l'absence éventuelle de cette propriété (c'est-à-dire « non nécessairement déterministe »).
Il est remarquable que tout automate fini peut être transformé, au moyen d'une opération qui peut éventuellement augmenter exponentiellement son nombre d'états, en un automate déterministe : c'est la déterminisation expliquée plus loin.
Les automates finis se rencontrent, dans une formulations proche, dans les circuits intégrés numériques, où l'entrée, l'état et le résultat sont des vecteurs de bits de taille fixe. Les machines de Moore et machines de Mealy sont des automates finis avec sortie. Dans les machines de Mealy, les actions (sorties) sont liées aux transitions, tandis que dans les machines de Moore, les actions sont liées aux états. Les transducteurs finis sont des automates avec sortie plus généraux.
Définitions formelles
Alphabet
Un alphabet est un ensemble, en général supposé fini et non vide. Ses éléments sont des lettres.
Mot
Un mot sur un alphabet est une suite finie d'éléments de . Un mot est noté par la juxtaposition de ses lettres. Ainsi, on écrit au lieu de . La longueur d'un mot est le nombre d'éléments qui le composent. La suite vide, mot de longueur 0, souvent notée , est appelée le mot vide. L'ensemble des mots sur est noté . La concaténation de deux mots et est le mot obtenu par juxtaposition. En particulier, . La concaténation est associative, et par conséquent est un monoïde.
Automate fini
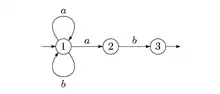
Un automate fini ou automate fini non déterministe (AFN) sur un alphabet est un quadruplet , où :
- est un ensemble fini d'états,
- est l'ensemble des transitions,
- est l'ensemble des états initiaux,
- et est un ensemble d'états finaux ou terminaux.
Une transition est composée d'un état de départ , d'une étiquette et d'un état d'arrivée . Un calcul (on dit aussi un chemin ou une trace) est une suite de transitions consécutives :
Son état de départ est , son étiquette est le mot et son état d'arrivée est . Un calcul est réussi si son état de départ est un des états initiaux, et son état d'arrivée est un des états terminaux.
Un mot est reconnu ou accepté par l'automate s'il est l'étiquette d'un calcul réussi. Le langage reconnu par l'automate est l'ensemble des mots reconnus. Un langage est reconnaissable s'il est reconnu par un automate fini.
Le langage reconnu par un automate est dénoté généralement par .
Automate complet, automate émondé
- Un automate est complet si pour tout état , et pour toute lettre , il existe au moins une transition partant de et portant l'étiquette .
- Un état est accessible s'il existe un chemin d'un état initial à .
- Un état est coaccessible s'il existe un chemin de à un état final.
- Un automate est accessible (coaccessible) si tous ses états sont accessibles (coaccessibles).
- Un automate est émondé si tous ses états sont à la fois accessibles et coaccessibles.
Automate fini déterministe
Un automate fini déterministe (AFD) sur un alphabet est un automate fini qui vérifie les deux conditions suivantes :
- il possède un seul état initial ;
- pour tout état , et pour toute lettre , il existe au plus une transition partant de et portant l'étiquette .
Pour un automate déterministe, la fonction de transition est la fonction partielle définie par : si est une transition. Si la fonction de transition est partout définie, l'automate est complet. La fonction de transition est étendue en une application (partielle) en posant
- pour tout état . Ici dénote le mot vide.
- pour tout état , tout mot et toute lettre .
Variations de notations
Il est d'usage de remplacer la notation par un simple point. On écrit alors à la place de , et la formule devient . Ceci montre aussi que la fonction de transition est une action du monoïde libre sur l'ensemble . On rencontre aussi la notation pour un automate déterministe, la fonction de transition étant sous-entendue (comme la loi de composition dans un groupe, par exemple). L'automate de la figure 3 est déterministe et incomplet. Son état initial est , et il possède un seul état final, l'état . Il reconnaît le langage sur l'alphabet .
On rencontre dans la littérature l'écriture d'un automate fini général sous forme de quintuplet
- .
Ici, l'alphabet de l'automate est inclus dans la spécification. La même façon d'inclure alphabet de définition dans la spécification se voit aussi pour les automates déterministes.
Exemples
- L'automate du début de l'article reconnaît les écritures binaire des entiers naturels multiples de 3. Par exemple, le nombre 18, dont l'écriture binaire est , est reconnu : le calcul est
.
On peut se convaincre qu'un entier mène, depuis l'état initial, à , ou , selon que le reste de sa division par 3 est 0, 1, ou 2.
- L'exemple suivant décrit un automate fini déterministe complet sur l'alphabet binaire , qui détermine si l'entrée contient un nombre impair de . Cet automate intervient dans la suite de Thue-Morse. L'automate est , avec , et la fonction de transition donnée par la table :
Chaque fois que l'on change d'état, la parité du nombre de change.
Extensions des automates finis (dont epsilon transitions)
Il existe plusieurs généralisation des automates finis, selon la nature des étiquettes que l'on autorise sur les transitions. Un automate asynchrone est un automate où l'étiquette d'une transition peut être le mot vide. Un telle transition est appelée une -transition ou transition spontanée[2], et on parle parfois d'automate à -transition. D'autres généralisations autorisent, comme étiquettes, des mots composés de plusieurs lettres. Enfin, une généralisation encore plus large permet comme étiquettes des langages rationnels, représentés par des expressions régulières. Toutes ces extensions n'augmentent pas la puissance des automates finis : un langage reconnu par une quelconque de ces extensions est reconnaissable par un automate fini, et même par un automate fini déterministe.
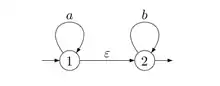
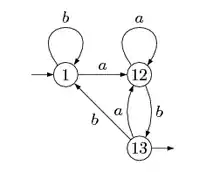
Un automate asynchrone est un automate fini autorisé à posséder des transitions étiquetées par le mot vide, appelées des -transitions. L'automate de la figure 6 est asynchrone.
L'élimination des -transitions se fait par un algorithme de fermeture transitive comme suit :
- Pour chaque chemin d'un état à un état formé de -transitions, et pour chaque transition de à un état portant une lettre , ajouter une transition de à d'étiquette ;
- Pour chaque chemin d'un état à un état terminal formé de -transitions, ajouter à l'ensemble des états terminaux ;
- Supprimer les -transitions.
Dans l'exemple de la figure 6, on ajoute la transition dans la première étape, et on déclare que est état final dans la deuxième étape. On obtient l'automate de la figure 7.
Opérations sur les automates
Déterminisation d'un automate fini
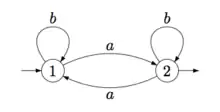
Il est toujours possible, à partir d'un automate fini non déterministe , de construire un automate fini déterministe reconnaissant le même langage :
Théorème — Pour tout automate fini , il existe un automate fini déterministe reconnaissant le même langage.
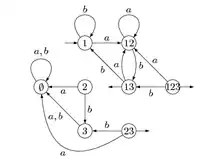
La méthode de construction est appelée la construction par sous-ensembles en français, et powerset construction en anglais.
Soit un automate fini sur un alphabet .
On construit l'automate comme suit :
- l'ensemble d'états de est l'ensemble des parties de l'ensemble ;
- l'état initial de est ;
- les états terminaux de sont les parties de qui ont une intersection non vide avec ;
- la fonction de transition de est définie, pour et , par
- .
L'automate est déterministe par construction.
Pour l'exemple de la figure 2, on obtient l'automate de la figure 4. Bien entendu, seuls les quatre états du haut sont utiles et même l'état peut être supprimé, puisqu'il n'est pas accessible. L'automate accessible déterminisé est celui de la figure 5.
Le nombre d'états de l'automate déterminisé peut être exponentiel par rapport au nombre d'états de l’automate de départ[3],[4].
Union, étoile etc.
Soit (respectivement ) l'automate fini reconnaissant le langage dénoté par l'expression rationnelle (respectivement ). Les constructions sont les suivantes (d'autres constructions existent, évitant l'introduction d'-transitions :
- Automate pour la réunion :
Il suffit de faire la réunion disjointe des automates et . Une variante consiste à introduire un nouvel état initial, et des -transitions de cet état vers les états initiaux des deux automates. - Automate pour le produit :
L'automate a pour états les états de et de . Les états initiaux sont ceux de , les terminaux sont ceux de . Les transitions sont celles de et de , et de plus des -transitions des états terminaux de vers les états initiaux de - Automate pour l'étoile :
On part de l'automate que l'on augmente de deux états et . On ajoute des -transitions
— de à tout état initial de
— de tout état final de à
— de à et de à .L'état (resp. ) est l'état initial (resp. final) de .
- Automate transposé On peut aussi construire un automate qui reconnaît les miroirs des mots d'un langage, c'est l'automate transposé ou automate miroir.
Produit direct et intersection
Soient et deux automates finis. Le produit direct ou produit cartésien des deux automates est l’automate
- ,
où les transitions de sont les triplets
- ,
avec et .
Le langage reconnu par est l’intersection des langages reconnus par et . C'est pourquoi on rencontre aussi la notation à la place .
Le théorème de Kleene
Le mathématicien Stephen C. Kleene a démontré que les langages reconnus par les automates finis sont exactement les langages qui peuvent être décrits par les expressions rationnelles. De manière plus concise, il y a égalité entre la famille des langages rationnels et la famille des langages reconnaissables sur un alphabet fini donné.
De plus, la démarche est constructive : pour toute expression rationnelle, on peut construire un automate fini (déterministe ou non) qui reconnaisse cette expression ; de même, pour tout automate fini (déterministe ou non), on peut exprimer sous forme d'une expression rationnelle le langage qu'il reconnaît.
Expressions rationnelles et langages rationnels
Les expressions rationnelles, ou expressions régulières sont des expressions qui décrivent les langages rationnels. Le terme expression régulière est antérieur, et les langages décrits par ces expressions sont naturellement aussi appelés langages réguliers.
Les expressions rationnelles, plus ou moins étendues, servent notamment à la recherche de motifs dans un texte.
Une expression rationnelle sur un alphabet est soit :
- Un symbole dénotant l'ensemble vide ;
- un symbole dénotant le mot vide : ou ;
- une lettre de l'alphabet ;
- une réunion (ou somme, en notation algébrique) de deux expressions rationnelles et , notée ou
- une concaténation (ou un produit, en notation algébrique) de deux expressions rationnelles et , notée ou simplement
- une répétition, ou étoile, ou itération, d'une expression rationnelle notée .
On distingue soigneusement l'expression rationnelle, qui est une simple expression, c'est-à-dire une chaîne de caractères qui représente un arbre d'expression, du langage que représente cette expression appelé le langage dénoté par l'expression. Ce langage est noté et est défini récursivement, à partir de l'expression :
Par exemple,
Des expressions aux automates
Il existe plusieurs méthodes pour construire un automate fini à partir d'une expression rationnelle
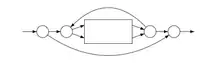
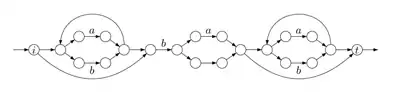 Automate obtenu par la méthode de Thompson pour l'expression .
Automate obtenu par la méthode de Thompson pour l'expression .
Méthode de Thompson
La méthode de Thompson[5] a été utilisée par Ken Thompson dans l'implémentation de la commande grep du système Unix.
On construit récursivement des automates pour les composants d'une expression. La forme particulière des automates permet de les combiner avec une grande facilité. L'automate obtenu est non déterministe asynchrone.
La construction de Thompson peut être optimisée ; une construction attribuée à Ott et Feinstein[6] introduit les variantes que voici pour minimiser le nombre de epsilon transitions:
- Pour l’union, au lieu d’introduire deux nouveaux états, on fusionne les états initiaux et finaux
- Pour la concaténation, on fusionne l’état final du premier avec l’état initial du second
- Pour l’étoile, un circuit formé uniquement de epsilon transitions est supprimé et les états du circuit fusionnés.
Un automate nommé « follow automaton » et introduit par Ilie et Yu[6] pousse plus loin encore l'élimination des epsilon-transitions.
Méthode de Glushkov
La méthode de Glushkov[7] est attribuée à l'informaticien Glushkov, permet de construire un automate non déterministe de même taille (nombre d'états) que la taille (nombre de symboles) de l'expression rationnelle.
Il a été observé[8] que l'automate de Glushkov est le même que l'automate obtenu en supprimant les -transitions de l'automate de Thompson.
Méthode des dérivées
La méthode des quotients ou résiduels ou dérivées, est due à Brzozowski[9] On forme les quotients (ou résiduels) successifs de l'expression. Il n'y en a qu'un nombre fini de différents, après application d'un certain nombre de règles de simplification qui sont l'associativité, la commutativité et l'idempotence de l'opération .
Aucune de ces méthodes ne donne directement l'automate minimal d'un langage. On peut aussi employer des constructions simples d'automates pour la réunion, le produit et l'étoile de langages, et opérer récursivement.
Des automates aux expressions
Il existe plusieurs algorithmes pour calculer, à partir d'un automate fini donné par son graphe, une expression rationnelle qui le représente. Ces algorithmes opèrent tous par réduction, en éliminant les états progressivement. La mise-en-œuvre diffère, selon que l'on traite les opérations successivement, comme la méthode de résolution des systèmes d'équations linéaires par la méthode de Gauss, ou récursivement par partition en blocs, comme la méthode de Conway. Une difficulté réside dans le fait que, selon le mode opératoire, le résultat ne donne pas la même expression, mais seulement des expressions équivalentes, donc des expressions différentes dénotant le même langage.
Systèmes d'équations linéaires

À tout automate, on peut associer un système d'équations linéaires dont les coefficients sont des parties de l'alphabet. On résout le système par une méthode similaire à la méthode d'élimination de Gauss[10], et qui est fréquemment appelé méthode d'élimination des variables[8]. L'ingrédient de base est ce qu'on appelle le lemme d'Arden.
Soit un automate fini sur un alphabet . Pour chaque état , soit le langage reconnu à partir de l'état , c'est-à-dire le langage reconnu en prenant pour état initial. On pose enfin . Ce sont les étiquettes des transitions de à . On a alors :
où
L'application du lemme d'Arden permet d'éliminer une à une les inconnues des équations de la forme précédente, et d'obtenir une expression explicite des et notamment des , ce qui détermine le langage reconnu par l'automate .
Exemple : Reprenons l'automate de la figure 7. Le système associé s'écrit :
La deuxième équation donne :
En reportant dans la première, on obtient :
et le lemme d'Arden donne :
Note : Les ensembles qui, dans les équations ci-dessus sont des parties de l'alphabet, peuvent être remplacés par des ensembles rationnels quelconques : les langages solutions sont toujours rationnels, à condition de prendre la plus petite solution dans le lemme d'Arden.
Méthode de Conway
Une méthode semblable est l'algorithme de Conway. Il opère de manière récursive, au moyen d'une partition en blocs de l’automate. La représentation choisie est matricielle, et la partition en blocs de l'automate se ramène à la partition en blocs de la matrice associée.
Méthode de Brzozowski et McCluskey
Encore une méthode d'élimination, cette méthode utilise de façon intensive la représentation graphique de l'automate. L'automate lui-même est généralisé, en autorisant, comme étiquettes des transitions, non seulement des lettres, mais des expressions régulières. Partant d'une automate fini, on élimine progressivement les états, et à la fin, on se retrouve avec un automate ayant une seule transition. L'étiquette de cette transition est une expression rationnelle pour le langage reconnu par l'automate.
Complexité en taille des opérations
Les opérations de passage d'une expression à l’automate et réciproquement ont une complexité en temps et en place qu'il est important de savoir évaluer, en théorie et pour les applications. Un article de Hermann Gruber et Markus Holzer[6] en fait un tour d'horizon. La mesure de la complexité d'un automate peut se faire en comptant le nombre d'états ou le nombre de transitions.
Pour un langage rationnel L sur un alphabet A, on note
- sc(L) le nombre minimal d'états dans un automate fini déterministe
- tc(L) le nombre minimal de transitions dans un automate fini déterministe
- nsc(L) le nombre minimal d'états dans un automate fini non déterministe
- ntc(L) le nombre minimal de transitions dans un automate fini non déterministe
pour un automate acceptant L. Les deux dernières mesures de complexité peuvent être indicées par ε, indiquant que l'on autorise les epsilon transitions. On a les inégalités suivantes, où |A| est la taille de l'alphabet :
- ,
- ,
Pour les expressions régulières, il y a plusieurs façons de les mesurer, selon que l'on compte le nombre de symboles de lettres, de lettres et symboles d'opération, ou lettres, symboles d'opération et parenthèses. On a les inégalités suivantes[6] :
- et
- et
- et
Ici la « taille » est le nombre total de symboles, y compris les lettres, opérations, parenthèses d'une expression, « pn » est le nombre de symboles sans les parenthèses, donc juste de lettres et symboles d’opérations (« pn » pour « polish notation »), et « largeur » est nombre total d’occurrences de lettres, donc sans les symboles d’opérations.
Grammaires et les langages rationnels
Les langages rationnels forment la classe la plus simple de la hiérarchie de Chomsky et sont, à ce titre, engendrés par des grammaires algébriques particulières, les grammaires linéaires droites ou grammaires linéaires gauches. Ce sont des grammaires où toutes les règles sont de la forme ou , avec un mot ne contenant pas de variable et des variables. (Pour les grammaires linéaire gauches, remplacer par .)
On construit, pour une grammaire linéaire droite , un automate fini (généralisé, avec des mots comme étiquettes) comme suit : les états de l'automate sont les variables de la grammaire, plus un état spécial . L'état initial est , le seul état final est . Chaque règle fournit une transition de vers d'étiquette , et chaque règle fournit une transition de vers d'étiquette .
Minimisation d'un automate fini
Deux automates finis sont équivalents s'ils reconnaissent le même langage. C'est un résultat remarquable de la théorie qu'il existe, pour tout automate fini, un seul automate fini déterministe minimal (c'est-à-dire ayant un nombre minimal d'état) qui est équivalent à l'automate donné. De plus, cet automate, appelé automate minimal, se calcule efficacement par l'algorithme de Moore ou l'algorithme de Hopcroft. L'unicité de l'automate ayant un nombre minimal d'état n'est plus vraie pour les automates non déterministes.
On peut ainsi décider de l'équivalence de deux automates en calculant, pour chacun, l'automate minimal déterministe correspondant, et en testant l'égalité des deux automates obtenus.
Monoïde de transition et monoïde syntaxique
Soit un automate fini déterministe complet sur un alphabet . Chaque mot définit une application donnée par
Ici l'argument de la fonction est noté à gauche de la fonction. On a
En effet . L'application est donc un morphisme de dans le monoïde des applications de dans lui-même. L'image est appelée le monoïde de transition de l'automate. Lorsque l'automate est minimal, le monoïde de transition est isomorphe au monoïde syntaxique du langage reconnu par l'automate.
Mise en œuvre
Un automate fini peut être représenté en utilisant une table de transition d'état. On le représente alors sous forme logicielle avec une matrice de transition d'état. Dans certains cas, il est plus avantageux d'utiliser une matrice creuse, ou un énorme switch qui distribue selon les états, et pour chaque état un autre switchs qui distingue les symboles d'entrée.
La réalisation d'automates finis se fait aussi, sous forme matérielle, par un dispositif de logique programmable appelé table logique programmable (en).
Notes
- Droste et al. 2009
- Terminologie de Sakarovitch 2003.
- En fait, on peut rencontrer à peu près toutes les situations envisageables. Il a été démontré (G. Jirásková. « Magic numbers and ternary alphabet », dans V. Diekert and D. Nowotka (éditeurs), Developments in Language Theory, Lecture Notes in Comput. Sci. 5583(2009) p. 300–311. Springer-Verlag) que, sur un alphabet à trois lettres, il existe, pour tous avec , un automate non déterministe minimal à états, pour lequel l'automate déterministe minimal équivalent a états.
- Oleg Lupanov a, en 1963, montré que la borne peut être atteinte : (en) Oleg B. Lupanov, « A comparison of two types of finite sources », Problemy Kibernetiki, vol. 9, , p. 321–326.
- Thompson 1968 ; elle est attribuée à McNaughton et Yamada dans Hopcroft et al. 2007.
- Gruber et Holzer 2015.
- Glushkov 1961.
- Sakarovitch 2003.
- Brzozowski 1964.
- Carton 2008.
Voir aussi
Articles connexes
Bibliographie
- Olivier Carton, Langages formels, calculabilité et complexité, [détail de l’édition] (lire en ligne)
- Manfred Droste, Werner Kuich et Heiko Vogler, Handbook of Weighted Automata, Springer-Verlag, , 608 p. (ISBN 978-3-642-01491-8)
- (en) John E. Hopcroft, Rajeev Motwani et Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley, , 3e éd. (ISBN 978-0-32146225-1)
- Jacques Sakarovitch, Éléments de théorie des automates, Vuibert, , 816 p. (ISBN 978-2-7117-4807-5)Traduction anglaise avec corrections : Elements of Automata Theory, Cambridge University Press 2009, (ISBN 9780521844253)
- Patrice Séébold, Théorie des automates : Méthodes et exercices corrigés, Vuibert, , 198 p. (ISBN 978-2-7117-8630-5)
- Hermann Gruber et Markus Holzer, « From Finite Automata to Regular Expressions and Back : A Summary on Descriptional Complexity », Int. J. Found. Comput. Sci., vol. 26, no 08, , p. 1009-1040 (DOI 10.1142/s0129054115400110).
Références historiques
- John A. Brzozowski, « Derivatives of regular expressions », J. Assoc. Comput. Mach., vol. 11, , p. 481–494
- Victor M. Glushkov, « The abstract theory of automata », Russian Math. Surveys, vol. 16, , p. 1–53
- Ken Thompson, « Regular expression search algorithm », Comm. Assoc. Comput. Mach., vol. 11, , p. 419–422
- Robert McNaughton et H. Yamada, « Regular expressions and state graphs for automata », IRE Trans. Electronic Computers, vol. EC-9, no 1, , p. 39-47 (DOI 10.1109/TEC.1960.5221603)
Liens externes
- L'histoire des automates finis a été décrite par Dominique Perrin dans l'article : Les débuts de la théorie des automates, paru dans Technique et science informatiques 1995, vol. 14, no 4, p. 409-433.
- Des outils informatiques permettent de générer des programmes afin de plus facilement définir des automates Hierarchical State Machine Compiler
- FSM: Open Source Finite State Machine Generation in Java by Alexander Sakharov FSM
- SMC: An Open Source State Machine Compiler that generates FSM for many languages as C, Python, Lua, Scala, PHP, Java, VB, etc SMC
- Portail de l'informatique théorique