Suite de Prouhet-Thue-Morse

En mathématiques, en informatique théorique, en combinatoire des mots et ses applications, la suite de Prouhet-Thue-Morse, également appelée suite de Thue-Morse, est une suite binaire — c'est-à-dire dont les termes valent 0 ou 1. Elle commence par :

t=0\;1\;10\;1001\;10010110\;1001011001101001\ldots

C'est une suite automatique (elle est calculable par un automate fini), uniformément récurrente (en particulier elle contient tous les mots binaires possibles[note 1]) et sans cube (aucun mot n'y est répété trois fois consécutivement).

Elle est répertoriée comme la suite A010060 de l'OEIS.

Histoire

La suite de Prouhet-Thue-Morse a été utilisée pour la première fois de façon implicite par le mathématicien français Eugène Prouhet en 1851, pour donner une solution à un problème de théorie des nombres appelé depuis le problème de Prouhet-Tarry-Escott[1].

Le mathématicien norvégien Axel Thue l'a découverte et utilisée dans un article publié en 1912 qui, avec un autre article datant de 1906, est l'article fondateur de la combinatoire des mots. Cet article a été longtemps méconnu. La suite a été redécouverte par Marston Morse en 1921. Morse l'a utilisée pour donner un exemple d'une suite uniformément récurrente (la définition est donnée plus loin) non périodique, résolvant ainsi un problème de géométrie différentielle.

Redécouverte dans le domaine des jeux

La suite a été redécouverte indépendamment plusieurs fois, pas toujours par des mathématiciens professionnels.

Au shogi

金

△ Koji Tanigawa

9	8	7	6	5	4	3	2	1
									a
									b
									c
									d
									e
									f
									g
									h
									i

▲ Kunio Yonenaga
飛 , 金 , 銀 , 歩 x 4

Le 8 mars 1983, une partie de shogi disputée entre Kunio Yonenaga et Kōji Tanigawa a fait apparaître une suite analogue à la suite de Prouhet-Thue-Morse[2]. La position ci-contre apparaît au coup 118 ; Tanigawa est dans une position désavantageuse car il a moins de matériel en main que Yonenaga et tente alors d'obtenir une nulle par triple répétition d'une séquence de coup[2]. Cependant dans cette position Yonenaga a plusieurs manières équivalentes de commencer une séquence amenant à la reproduction du diagramme : deux qui commencent par le parachutage d'un général d'or en h8 et une commençant par un général d'argent en g8[2]. En alternant deux de ces séquences selon une suite de Prouhet-Thue-Morse il est alors possible de forcer une séquence de coups arbitrairement longue sans que la partie soit nulle puisque la suite de Prouhet-Thue-Morse est sans cube (Yonenaga a choisi une autre séquence de coups ayant la même propriété)[2]. Yonenaga a alors pu prendre le temps de réfléchir à une manière de rompre la répétition à son avantage pour remporter la partie[2]. Comprenant cela Tanigawa a rompu lui-même la séquence 60 coups plus tard pour tenter de prendre l'avantage avant que son adversaire n'arrive à trouver le moyen de forcer la victoire, mais il finit par perdre la partie[2]. La règle du sennichite a été modifiée deux mois plus tard à la suite de cette partie : une partie est déclarée nulle après quatre répétitions d'une même position et ce quelles que soient les séquences aboutissant à ces répétitions de position[2].

Aux échecs

Max Euwe, un champion d'échecs et professeur de mathématiques, a découvert en 1929 une application analogue de cette suite aux échecs, prouvant, par ce biais, qu'il existe des parties infinies ne comportant pas de répétition immédiate d'une même séquence de coups par trois fois. En 1944, Marston Morse et Gustav Hedlund ont développé cet aspect.

Tirs au but au football

Les études des séances de tirs au but au football ont démontré un avantage statistique pour l’équipe qui effectue le premier tir. Pour corriger ce déséquilibre dû selon les chercheurs à la pression plus forte sur les tireurs de la deuxième équipe, l’économiste espagnol Ignacio Palacios-Huerta a proposé d’alterner les tirs selon la suite de Prouhet-Thue-Morse. C’est-à-dire, A et B les deux équipes et A étant celle qui tire la première^[pas clair], après le premier tir de l’équipe A, on effectuerait deux tirs de l’équipe B, puis un de A et un de B, puis deux de A, puis un de B, les huit premiers tirs faisant un cycle complet qui recommence de la même manière au neuvième tir. Selon Palacios-Huerta, cette méthode réduirait le déséquilibre statistique actuellement constaté de 60,6%-39,4 % à 51%-49 % en faveur de l’équipe A[3].

La réalité statistique de cet avantage à tirer en premier est controversée. Voir les références données dans l'article sur les tirs au but.

Définitions

Il y a plusieurs manières équivalentes de définir cette suite.

Définition par récurrence

La suite de Prouhet-Thue-Morse est la suite $t=(t_{n})$ qui satisfait $t_{0}=0$ et

{\begin{array}{lcl}t_{2n}&{\!\!\!=\!\!\!}&t_{n}\\t_{2n+1}&{\!\!\!=\!\!\!}&1-t_{n}\end{array}}

pour tous les entiers naturels n. Cette définition peut s'interpréter comme suit : si l'on ne conserve, dans la suite $t$ , que les termes d'indices pairs, on retrouve la suite $t$ ; si en revanche on ne garde que les termes d'indices impairs, on obtient la suite opposée, où les $0$ et $1$ ont été échangés.

Autre récurrence

Construction de la suite de Prouhet-Thue-Morse : chaque bloc est obtenu par concaténation du bloc précédent avec son opposé.

Soient $u_{n}$ et $v_{n}$ les suites de mots définis par :

{\begin{array}{lcl}u_{0}&{\!\!\!=\!\!\!}&0\\u_{n+1}&{\!\!\!=\!\!\!}&u_{n}v_{n}\end{array}}\quad {\begin{array}{lcl}v_{0}&{\!\!\!=\!\!\!}&1\\v_{n+1}&{\!\!\!=\!\!\!}&v_{n}u_{n}.\end{array}}

Alors

t=\lim _{n\to \infty }u_{n}=0v_{0}v_{1}v_{2}\cdots v_{n}\cdots

On a en fait $v_{n}={\overline {u_{n}}}$ , où le mot surligné est l'opposé (obtenu en échangeant les $0$ et $1$ ). C'est cette méthode qui est illustrée dans la figure.

Cette construction provient de la relation $t_{2^{n}+k}=1-t_{k}$ pour tous naturels $n$ et $k$ .

Définition directe

Automate de Prouhet-Thue-Morse.

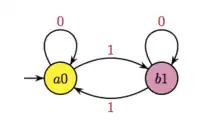
$t_{n}$ est égal à la somme, modulo 2, des chiffres dans le développement binaire de $n$ . Par exemple, $(18)_{2}=10010$ , et donc $t_{18}=0$ . Ce calcul est réalisé par l'automate de Prouhet-Thue-Morse : partant de l'état initial, on suit les transitions indiquées par les bits du développement binaire. L'état d'arrivé, selon qu'il est jaune ou rose, indique que la valeur de la suite est 0 ou 1. Pour $(18)_{2}=10010$ , on obtient :

a0{\xrightarrow {1}}b1{\xrightarrow {0}}b1{\xrightarrow {0}}b1{\xrightarrow {1}}a0{\xrightarrow {0}}a0

et la valeur est donc 0.

Définition par morphisme

La suite $t$ est obtenue aussi en itérant le morphisme $\mu$ appelé parfois le morphisme de Thue-Morse suivant :

{\begin{array}{lcl}0\mapsto 01\\1\mapsto 10\end{array}}

Les premières itérations à partir de $0$ donnent :

{\begin{array}{lcl}\mu ^{0}(0)=0\\\mu ^{1}(0)=01\\\mu ^{2}(0)=0110\\\mu ^{3}(0)=01101001\\\mu ^{4}(0)=0110100110010110\end{array}}

Si l'on itère à partir de 1, on obtient la suite opposée.

Définition par fonction génératrice

La fonction génératrice de la suite $((-1)^{t_{n}})=(1-2t_{n})$ est donnée par

\sum _{n=0}^{\infty }(-1)^{t_{n}}X^{n}=\prod _{n=0}^{\infty }(1-X^{2^{n}})

Donc pour $t$ elle même :

$\sum _{n=0}^{\infty }t_{n}X^{n}={1 \over 2}\left({\frac {1}{1-X}}-\prod _{n=0}^{\infty }(1-X^{2^{n}})\right)$

Propriétés

La suite de Prouhet-Thue-Morse est uniformément récurrente : pour tout entier $n$ , il existe un entier $N$ tel que tout facteur de longueur $N$ contient tous les facteurs de longueur $n$ .
La suite de Prouhet-Thue-Morse est sans cube : aucun bloc n'est répété trois fois consécutivement. En revanche, elle contient des carrés arbitrairement longs. Axel Thue a prouvé que la suite est sans chevauchement : aucun bloc n'est de la forme $axaxa$ , où $a$ est un des symboles $0$ ou $1$ et $x$ est un bloc.
La constante de Prouhet-Thue-Morse est le nombre $\tau \,$ dont le développement binaire est la suite de Prouhet-Thue-Morse, c’est-à-dire le nombre $\tau =\sum _{i=0}^{\infty }{\frac {t_{i}}{2^{i+1}}}=0{,}412\,454\,033\,640\ldots$ C'est un nombre transcendant.

Produits infinis associés à la suite

J.P Allouche a démontré que le produit infini : $\prod _{n\geqslant 0}\left({\frac {2n+1}{2n+2}}\right)^{(-1)^{t_{n}}}$ est semi-convergent et a pour valeur $1/{\sqrt {2}}$ [4]^,[5].

Nota : Ce produit infini a une définition naturelle, car si l'on considère la suite de fractions $u_{1}={\frac {1}{2}},u_{2}={\frac {\frac {1}{2}}{\frac {3}{4}}},u_{3}={\frac {\frac {1}{2}}{\frac {3}{4}}}/{\frac {\frac {5}{6}}{\frac {7}{8}}}$ , alors $u_{n}=$ $\prod _{k=0}^{2^{n-1}-1}\left({\frac {2k+1}{2k+2}}\right)^{(-1)^{t_{k}}}$ , et par conséquent, $\lim u_{n}={1 \over {\sqrt {2}}}$ .

Démonstration

La fraction $u_{n}$ s'obtient en multipliant la fraction précédente par l'image de cette fraction obtenue en échangeant numérateurs et dénominateurs, avec les mêmes entiers augmentés de $2^{n-1}$ , règle reproduisant exactement la règle de construction de la suite de Prouhet-Thue-Morse.

Donc $u_{n}=\prod _{k=0}^{2^{n}-1}(k+1)^{(-1)^{t_{k}}}$ ; en regroupant les termes deux à deux, on obtient $u_{n}=\prod _{k=0}^{2^{n-1}-1}(2k+1)^{(-1)^{t_{2k}}}(2k+2)^{(-1)^{t_{2k+1}}}=\prod _{k=0}^{2^{n-1}-1}\left({\frac {2k+1}{2k+2}}\right)^{(-1)^{t_{k}}}$ .

En utilisant le produit infini de Wallis, on en déduit :

\prod _{n\geqslant 0}{\left({\frac {2n+1}{2n+2}}\right)}^{2t_{n}}\left({\frac {2n+3}{2n+2}}\right)={\frac {2{\sqrt {2}}}{\pi }}

[6],

\prod _{n\geqslant 0}{\left({\frac {2n+1}{2n+2}}\right)}^{2(1-t_{n})}\left({\frac {2n+3}{2n+2}}\right)={\frac {\sqrt {2}}{\pi }}

[6].

Le produit infini $\prod _{n\geqslant 1}\left({\frac {2n}{2n+1}}\right)^{(-1)^{t_{n}}}$ est également convergent, mais on ne connait pas sa valeur, ni son statut algébrique ; voir la suite A086744 de l'OEIS.

Suite de Prouhet-Thue-Morse et nombres normaux

Complexité combinatoire

La complexité combinatoire de la suite de Prouhet-Thue-Morse est par définition la fonction $c_{t}(n)$ qui donne le nombre de facteurs (ou blocs) distincts de longueur n de la suite. Les premières valeurs de cette fonction sont

Fonction de complexité de la suite de Prouhet-Thue-Morse
$n$	0	1	2	3	4	5	6	7	8	9	10
$c_{t}(n)$	1	2	4	6	10	12	16	20	22	24	28

C'est la suite A005942 de l'OEIS. La formule qui donne les valeurs est la suivante : Pour $n\geq 1$ , soit $k\geq 0$ l'entier tel que $2^{k}+1\leq n\leq 2^{k+1}$ , et soit $r$ tel que $n=2^{k}+r$ , avec $1\leq r\leq 2^{k}$ . Alors

c_{t}(n)={\begin{cases}3\cdot 2^{k}+4(r-1)&{\text{si }}1\leq r\leq 2^{k-1},\\4\cdot 2^{k}+2(r-1)&{\text{si }}2^{k-1}+1\leq r\leq 2^{k}.\end{cases}}

Comme toutes les fonctions de complexités des suites automatiques, cette fonction croît au plus linéairement. De fait, on peut prouver que $c_{t}(n)\leq {\frac {10}{3}}n$ .

Suite aux positions carrées

La suite de Prouhet-Thue-Morse n'est pas une suite normale, puisque dans une suite normale tous les facteurs apparaissent, et deux facteurs de même longueur apparaissent avec la même fréquence asymptotique. Mais il en va autrement d'une suite associée à la suite de Prouhet-Thue-Morse $t$ , qui est la suite extraite aux positions qui sont des carrés. C'est la suite $u$ donnée par :

u_{n}=t_{n^{2}}

La suite commence par

0,1,1,0,1,1,0,1,1,1,1,1,0,0,1,0,1,

C'est la suite A010060 de l'OEIS. Cette suite a fait l'objet de plusieurs études : Allouche et Shallit [7] se demandent si la complexité de la suite $u$ est maximale, c'est-à-dire si le nombre $c_{u}(n$ ) de facteurs de longueur $n$ de la suite $u$ vérifie $c_{u}(n)=2^{n}$ . Une réponse positive à cette question est donnée par Moshe en 2007[8]. Mauduit et Rivat montrent[9] que les 0 et les 1 apparaissent dans $u$ avec la même fréquence asymptotique $1/2$ . Ceci à son tour résout une conjecture longtemps ouverte de Gelfond[10]. Un résultat, annoncé par Drmota, Mauduit, et Rivat en 2013 et publié en 2019, dit[11] que la suite $u$ est normale. D'autres suites ont cette propriété, comme la suite de Rudin-Shapiro[12].

Suite bilatère

La suite de Prouhet-Thue-Morse peut être étendue en une suite indexée par $\mathbb {Z}$ en posant

t_{-i}=t_{i-1}\quad (i\geq 1)

On obtient donc (un point central est placé avant $t_{0}$ ) la suite :

\dotso 0110100110010110.01101001100101101001011001101001\dotso

Cette suite est encore une suite sans chevauchement. De plus, le système dynamique engendré par cette suite est exactement l'ensemble des suites bilatères sans chevauchement.

Notes et références

Notes

La propriété est plus forte que ça, lire plus loin dans l'article.

Références

M. E. Prouhet, Mémoire sur quelques relations entre les puissances des nombres, C. R. Acad. Sci. Paris, série I, 33, (1851), 225
(en) [vidéo] How to play Shogi(将棋) -Lesson#15- Repetition("Sen-nichi-te") sur YouTube, à partir de 3 min 26s.
Faites votre choix : Goldman Sachs ou Franck Ribéry ?, numéro 21 (9 juin 2016) de Lab Hebdo écrit par Sylvain Frochaux.
(en) Jean-Paul ALLOUCHE, « Thue, Combinatorics on words, and conjectures inspired by the Thue-Morse sequence », Journal de théorie des nombres de Bordeaux, Tome 27, no 2,‎ 2015, p. 381
Jean Moussa, « Quelques propriétés associées à la suite de Prouhet-Thue-Morse », Bulletin de l'APMEP,‎ mars-avril 2016, p. 199-206 (lire en ligne)
Allouche et Shallit 2003, page 204
Allouche et Shallit 2003, Problem 10.12.7.
Y. Moshe, « On the subword complexity of Thue-Morse polynomial extractions », Theoret. Comput. Sci., vol. 38,‎ 2007, p. 318–329.
C. Mauduit et J. Rivat, « La somme des chiffres des carrés », Acta Math., vol. 203,‎ 2009, p. 107-148.
A. O. Gelfond, « Sur les nombres qui ont des propriétés additives et multiplicatives données », Acta Arith., vol. 13,‎ 1967/1968, p. 259-265.
Michael Drmota, Christian Mauduit et Joël Rivat, « Normality along squares », Journal of the European Mathematical Society, vol. 21, n^o 2,‎ 2019, p. 507–548 (DOI 10.4171/JEMS/843, lire en ligne).
Clemens Müllner, « The Rudin–Shapiro Sequence and Similar Sequences Are Normal Along Squares », Canadian Journal of Mathematics, vol. 70, n^o 5,‎ 2018, p. 1096–1129 (DOI 10.4153/CJM-2017-053-1).

Bibliographie

Jean-Paul Delahaye, « Des mots magiques infinis », Pour la Science, n^o 347,‎ septembre 2006, p. 90-95 (lire en ligne)
Jean-Paul Delahaye, Mathématiques pour le plaisir, Belin - Pour La Science, janvier 2010 (lire en ligne), « Des mots magiques infinis (même article que le précédent) », p. 160-167
Jean-Paul Delahaye, « Des suites fractales d'entiers », Pour la Science, n^o 531,‎ janvier 2022, p. 82-83 (lire en ligne)
Fabien Aoustin, « La très riche suite de Prouhet-Thue-Morse », Bibliothèque Tangente,‎ décembre 2021, p. 90-94 (lire en ligne )
(en) Jean-Paul Allouche et Jeffrey Shallit, Automatic sequences : Theory, applications, generalizations, Cambridge, Cambridge University Press, 2003, 571 p. (ISBN 0-521-82332-3, Math Reviews 1997038)
Shyam Narayanan, « Functions on antipower prefix lengths of the Thue–Morse word », Discrete Mathematics, vol. 343, n^o 2,‎ 2020, article n^o 111675 (DOI 10.1016/j.disc.2019.111675)

Articles connexes

Liens externes

(en) Jean-Paul Allouche et Jeffrey O. Shallit, The Ubiquitous Prouhet-Thue-Morse Sequence. Contient de nombreuses propriétés et références.
(en) Eric W. Weisstein, « Thue-Morse Sequence », sur MathWorld. Des applications supplémentaires.

Portail des mathématiques
Portail de l'informatique théorique
Portail des jeux

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] La propriété est plus forte que ça, lire plus loin dans l'article.

[2] M. E. Prouhet, Mémoire sur quelques relations entre les puissances des nombres, C. R. Acad. Sci. Paris, série I, 33, (1851), 225

[hidetchi-3] (en) [vidéo] How to play Shogi(将棋) -Lesson#15- Repetition("Sen-nichi-te") sur YouTube, à partir de 3 min 26s.

[4] Faites votre choix : Goldman Sachs ou Franck Ribéry ?, numéro 21 (9 juin 2016) de Lab Hebdo écrit par Sylvain Frochaux.

[5] (en) Jean-Paul ALLOUCHE, « Thue, Combinatorics on words, and conjectures inspired by the Thue-Morse sequence », Journal de théorie des nombres de Bordeaux, Tome 27, no 2,‎ 2015, p. 381

[6] Jean Moussa, « Quelques propriétés associées à la suite de Prouhet-Thue-Morse », Bulletin de l'APMEP,‎ mars-avril 2016, p. 199-206 (lire en ligne)

[:0-7] Allouche et Shallit 2003, page 204

[8] Allouche et Shallit 2003, Problem 10.12.7.

[9] Y. Moshe, « On the subword complexity of Thue-Morse polynomial extractions », Theoret. Comput. Sci., vol. 38,‎ 2007, p. 318–329.

[10] C. Mauduit et J. Rivat, « La somme des chiffres des carrés », Acta Math., vol. 203,‎ 2009, p. 107-148.

[11] A. O. Gelfond, « Sur les nombres qui ont des propriétés additives et multiplicatives données », Acta Arith., vol. 13,‎ 1967/1968, p. 259-265.

[DrmotaMauduit2018-12] Michael Drmota, Christian Mauduit et Joël Rivat, « Normality along squares », Journal of the European Mathematical Society, vol. 21, n^o 2,‎ 2019, p. 507–548 (DOI 10.4171/JEMS/843, lire en ligne).

[Müllner2018-13] Clemens Müllner, « The Rudin–Shapiro Sequence and Similar Sequences Are Normal Along Squares », Canadian Journal of Mathematics, vol. 70, n^o 5,‎ 2018, p. 1096–1129 (DOI 10.4153/CJM-2017-053-1).