Boucle d'oreille hawaïenne
En mathématiques, la boucle d'oreille hawaïenne, aussi appelée anneaux hawaïens[1], est un espace topologique obtenu par réunion d’une suite de cercles dans le plan Euclidien R2, qui sont tangents intérieurement et de rayon décroissant vers 0. Par exemple, on peut utiliser la famille des cercles de centre (1/n, 0) et de rayon 1/n pour tout entier naturel non nul n. Cet espace est homéomorphe au compactifié d'Alexandrov de l'union d'une famille infinie dénombrable d'intervalles ouverts.
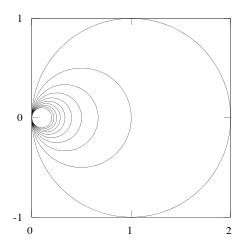
La boucle d'oreille hawaïenne peut être munie d'une métrique complète et elle est compacte. Elle est connexe par arcs mais pas semi-localement simplement connexe.
La boucle d'oreille hawaïenne est très similaire au bouquet d'une infinité dénombrable de cercles ; en d'autres termes, la rose (en) avec une infinité de pétales, mais ces deux espaces ne sont pas homéomorphes. La différence entre leurs topologies respectives est décelable dans le fait que, dans la boucle d'oreille hawaïenne, chaque voisinage ouvert du point d'intersection des cercles contient tous les cercles à un nombre fini près. On le voit aussi dans le fait que le bouquet n'est pas compact : le complément du point distingué est une union d'intervalles ouverts ; ajouter un petit voisinage ouvert du point distingué fournit un recouvrement ouvert n'admettant pas de sous-recouvrement fini.
Groupe fondamental
La boucle d'oreille hawaïenne n'est pas simplement connexe, étant donné que le lacet paramétrant un cercle n'est pas homotope à une simple boucle. Ainsi, elle possède un groupe fondamental G non trivial.
La boucle d'oreille hawaïenne H admet le groupe libre à une infinité dénombrable de générateurs comme sous-groupe propre de son groupe fondamental. G contient des éléments supplémentaires, qui découlent de lacets dont l'image n'est pas contenue dans un nombre fini de cercles de la boucle d'oreille hawaïenne ; en fait, certains d'entre eux sont surjectifs : par exemple, le chemin (défini sur [0, 1]) qui, pour tout entier naturel non nul n, « fait le tour » du nième cercle sur l'intervalle [2−n, 2−(n−1)].
Il a été démontré que G se plonge dans la limite projective des groupes libres à n générateurs, Fn, où l'application de recollement de Fn vers Fn−1 « tue » simplement le dernier générateur de Fn. Cependant, G n'est pas la limite projective complète, mais plutôt le sous-groupe dans lequel chaque générateur apparaît seulement un nombre fini de fois. Un exemple d'élément de la limite projective qui n'est pas un élément de G est un commutateur infini.
G est non dénombrable, et ce n'est pas un groupe libre. Alors que son abélianisé n'a pas de description simple connue, G possède un sous-groupe normal N tel que le produit direct d'un nombre infini de copies du groupe cyclique infini (le groupe de Baer-Specker (en)). Cela s'appelle l'abélianisation infinie ou abélianisation forte de la boucle d'oreille hawaïenne, puisque le sous-groupe N est généré par des éléments où chaque coordonnée (en pensant à la boucle d'oreille hawaïenne comme un sous-groupe de la limite projective) est un produit de commutateurs. Dans un sens, N peut être considéré comme la clôture du groupe dérivé.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Hawaiian earring » (voir la liste des auteurs).
- Boucles d’oreilles hawaïennes sur Analysis situs.
Bibliographie
- (en) J. W. Cannon, G. R. Conner (2000), « The big fundamental group, big Hawaiian earrings, and the big free groups », Topology and its Applications 106 (3) : 273–291, DOI:10.1016/S0166-8641(99)00104-2.
- (en) G. Conner, K. Spencer (2005), « Anomalous behavior of the Hawaiian earring group », Journal of Group Theory 8 (2) : 223–227, DOI:10.1515/jgth.2005.8.2.223.
- (en) [PDF] K. Eda (en) (2002), « The fundamental groups of one-dimensional wild spaces and the Hawaiian earring », Proceedings of the American Mathematical Society 130 (5): 1515–1522, DOI:10.1090/S0002-9939-01-06431-0.
- (en) Eda, K.; Kawamura, K. (2000), « The singular homology of the Hawaiian earring », Journal of the London Mathematical Society 62 (1): 305–310, DOI:10.1112/S0024610700001071.
- (en) [PDF] Fabel, P. (2005), « The topological Hawaiian earring group does not embed in the inverse limit of free groups », Algebraic & Geometric Topology 5: 1585–1587, DOI:10.2140/agt.2005.5.1585.
- (en) Morgan, J. W.; Morrison, I. (1986), « A van Kampen theorem for weak joins », Proceedings of the London Mathematical Society 53 (3): 562–576, DOI:10.1112/plms/s3-53.3.56].
- Portail des mathématiques