Centre azote-lacune

Un centre azote-lacune, ou centre NV, est l'un des nombreux types de défauts ponctuels présents dans la structure cristalline du diamant. Il résulte de la juxtaposition d'une lacune au contact d'un atome d'azote substitutionnel. Une telle structure présente des propriétés de photoluminescence qui peuvent aisément être observées pour un centre particulier, notamment ceux qui sont chargés négativement (centres NV−). Le spin des électrons localisés à l'échelle atomique au niveau des centre NV peut être contrôlé à température ambiante en appliquant un champ magnétique, un champ électrique, un rayonnement microonde ou visible, ou un ensemble de ces stimuli, ce qui provoque de fortes résonances avec l'intensité et la longueur d'onde de la photoluminescence. Ces résonances peuvent être expliquées à partir du spin des électrons par des phénomènes tels que l'intrication quantique, l'interaction spin-orbite et les oscillations de Rabi, et analysés à l'aide de théories avancées en optique quantique. Un centre NV peut être vu comme l'unité de base d'un ordinateur quantique et ouvre la voie à des applications à des domaines novateurs en électronique et en sciences numériques comme la cryptographie quantique, la spintronique ou encore les masers.

Schéma d'un centre azote-lacune dans un cristal de diamant.

Structure
(en) En bas : mise en évidence par photoluminescence de centres NV− (points verts à droite) par application d'une tension de 20 V à une diode Schottky plane ; le dispositif de l'expérience est représenté en haut[1].

Un centre azote-lacune est un type de défaut ponctuel dans un cristal de diamant formé par la juxtaposition d'une lacune et d'un atome d'azote en substitution d'un atome de carbone.

On connaît deux états de charge pour ce défaut cristallin, l'état neutre NV0 et l'état négatif NV−, déterminés à partir d'études spectroscopiques faisant appel à l'absorption optique[2],[3], la photoluminescence[4] (PL), la résonance paramagnétique électronique[5],[6],[7] (EPR) et la détection optique de résonance magnétique (en)[8] (ODMR), laquelle peut être vue comme une technique hybride de PL et d'EPR ; c'est l'EPR qui fournit cependant l'essentiel des informations.

Un atome d'azote possède cinq électrons de valence. Trois d'entre eux forment des liaisons covalentes avec des atomes de carbone voisins, tandis que deux forment un doublet non liant. Une lacune voisine d'un atome d'azote possède trois électrons non appariés, un par atome de carbone voisin ; deux d'entre eux forment une liaison quasi covalente tandis que le troisième demeure non apparié, l'ensemble conservant une symétrie axiale C3v de sorte que les électrons appariés et non appariés demeurent indistincts autour de la lacune.

L'état NV0 a ainsi un électron non apparié et est paramagnétique. Les signaux de résonance électronique paramagnétique de centres NV0 n'ont cependant pas été observés, probablement parce que les signaux à partir de l'état fondamental sont trop larges pour être détectés par EPR[9].

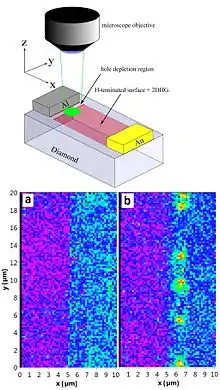
On peut obtenir un centre NV− à partir d'un centre NV0 en modifiant le niveau de Fermi, ce qu'on réalise en appliquant une tension électrique extérieure à une jonction p-n réalisée par dopage du diamant, par exemple dans une diode Schottky[1]. Un électron supplémentaire vient se loger dans la lacune et peut s'apparier avec l'électron non apparié qui s'y trouve en formant une paire de spin S=1. C'est cet état qui est souvent désigné comme « le centre azote-lacune », car l'état neutre n'a pas encore été exploré.

Les centres NV sont orientés au hasard dans le cristal de diamant. Des techniques d'implantation ionique peuvent permettre de les créer dans des positions prédéterminées[10].

Production

On obtient des centres azote-lacune généralement à partir de défauts ponctuels dits de type C (C-nitrogen centers en anglais) en les soumettant à une irradiation suivie d'un recuit au-dessus de 700 °C[2]. Il est possible d'utiliser un grand nombre de particules de haute énergie pour réaliser cette irradiation, comme des électrons, des protons, des neutrons, des ions et des photons gamma. Cette irradiation crée des lacunes dans le réseau cristallin, qui sont l'un des constituants des centres NV. Ces lacunes ne se déplacent pas à température ambiante, et un recuit est nécessaire pour permettre leur mobilité dans le cristal afin de les placer au contact d'un atome d'azote substitutionnel. Ces derniers exercent en effet une contrainte sur le réseau cristallin[11] qui attire les lacunes[12] et forme des centres NV.

  • Conversion d'une substitution d'azote de type C en centre NV.
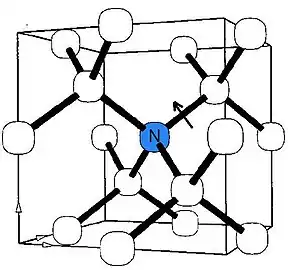
  • Défaut ponctuel de type C.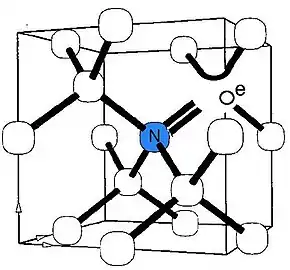
  • Centre NV−.

Au cours de la croissance du cristal de diamant par dépôt chimique en phase vapeur (CVD), une fraction infime des impuretés d'azote (généralement moins de 0,5 %) capturent des lacunes produites lors de la synthèse plasma. Ces centres azote-lacune sont alignés préférentiellement le long de la direction de croissance[13].

Le diamant est connu pour avoir de fortes contraintes dans son réseau cristallin. Ces contraintes séparent et déplacent les transitions optiques des centres individuels, ce qui élargit les raies spectrales produites par plusieurs centres[2]. Il est par conséquent nécessaire de soigner la qualité des matériaux destinés aux travaux de recherche afin de pouvoir distinguer les raies NV très étroites avec la précision requise par la plupart des expériences — environ 10 MHz[14] : on choisit des diamants naturels très purs et d'excellente qualité ou de préférence des diamants synthétiques de type IIa. La plupart d'entre eux ont déjà suffisamment de centres NV pour être directement utilisables, sinon ils sont irradiés avec des particules de haute énergie puis traités thermiquement pour recuit. Le choix de l'irradiation permet d'ajuster la concentration de centres NV afin que chacun d'entre eux soit séparé du voisin par une distance micrométrique. Les centres NV peuvent ensuite être étudiés individuellement à l'aide de microscopes optiques ou, mieux, de microscopes optiques en champ proche (NSOM) à résolution submicrométrique[8],[15].

Propriétés optiques fondamentales
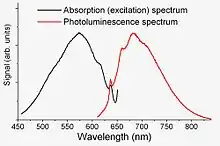
(en) Spectre d'absorption et spectre d'émission d'un centre NV− du diamant à 300 K.

Les centres NV− émettent une forte lumière rouge lorsqu'ils sont excités par des sources de lumière visible, comme des lasers à ions d'argon ou de krypton (en), des lasers Nd:YAG à doublement de fréquence, des lasers à colorants ou des lasers He-Ne. Il est également possible de les exciter à des énergies inférieures à celle de zéro émission de phonons[16]. L'illumination par laser convertit également certains centres NV− en centres NV0[4]. L'émission est très rapide, avec un temps de relaxation de l'ordre de 10 ns[17],[18]. L'élargissement thermique fait que les raies observées sont très diffuses, mais leur netteté s'améliore considérablement en refroidissant les centres NV− à l'azote liquide, voire à l'hélium liquide, ce qui permet de ramener leur largeur à quelques mégahertz.

La luminescence des centres NV− demeure remarquablement stable au cours du temps, alors que de nombreuses autres sources lumineuses moléculaires pâlissent après l'émission de 106 à 108 photons ; au contraire, les centres NV− ne pâlissent pas à température ambiante[8],[15].

Ces propriétés font que la technique idéale pour étudier les centres NV− est la microscopie confocale, et ce aussi bien à température ambiante qu'à basse température. En particulier, le fonctionnement à basse température est nécessaire pour étudier spécifiquement la raie zéro phonon (ZPL).

Altération des niveaux d'énergie par champs extérieurs
Schéma des niveaux d'énergie d'un centre NV−. Les transitions électroniques entre l'état fondamental 3E et l'état excité 3E, séparés par 1,945 eV (637 nm), sont observables par absorption et luminescence. L'état 3A est séparé par 1 027 G[5],[6] (environ 12 µeV) et l'état 3E est séparé par 508 G[19] (environ 5,9 µeV). Les nombres 0 et ±1 indiquent la valeur du spin.

La structure des niveaux d'énergie des centres azote-lacune du diamant a été déterminée en combinant des calculs théoriques, des mesures optiques et des résultats acquis par résonance paramagnétique électronique. La désignation des niveaux d'énergie fait appel à la théorie des groupes, et plus particulièrement aux symétries moléculaires du groupe ponctuel C3V du centre NV. Les nombres 3 et 1 des désignations 3A et 1A représentent la multiplicité de spin, c'est-à-dire le nombre d'états de spin possibles du défaut, allant de –S à S pour un total valant 2S + 1. Les valeurs de spin pour S = 1 peuvent être −1, 0 ou 1.

En l'absence de champ magnétique extérieur, l'état fondamental et l'état excité sont séparés par l'interaction magnétique entre les deux électrons non appariés du centre NV : l'énergie de ces électrons est supérieure lorsque leurs spins sont parallèles (ms ± 1) que lorsque leurs spins sont antiparallèles (ms = 0). Plus ces électrons sont éloignés l'un de l'autre, plus leur énergie d'interaction décroît (d'un facteur voisin de 1/r3)[6]. La limite inférieure de résolution dans l'état excité peut ainsi être vue en termes de limite supérieure de séparation des électrons dans cet état. Quand un champ magnétique extérieur est appliqué sur un centre NV−, il n'affecte pas l'état ms = 0, ni l'état 1A, car leur spin résultant est S = 0, mais il sépare les niveaux ms ± 1. Si un champ magnétique est orienté le long de l'axe du défaut avec une intensité de 1 027 G (ou 508 G), alors l'énergie des états ms = −1 et ms = 0 s'égalise, aussi bien à l'état fondamental qu'à l'état excité : ils interagissent alors fortement du fait d'une polarisation du spin, ce qui affecte fortement l'intensité de l'absorption optique et de la luminescence impliquant les transitions électroniques entre ces états[19].

Les transitions entre états électroniques font intervenir un photon, qui ne peut modifier le spin total : les transitions optiques doivent donc conserver le spin total et ne peuvent se produire qu'entre niveaux de même spin total. Pour cette raison, les transitions 3E ↔ 1A et 1A ↔ 3A ne sont pas radiatives et tarissent la luminescence. Alors que la transition ms = −1 (état excité) ↔ ms = 0 (état fondamental) est interdite en l'absence de champ magnétique, elle devient possible lorsqu'un champ magnétique mélange les niveaux ms = −1 et ms = 0 à l'état fondamental. Une conséquence visible de ce phénomène est que l'intensité de la luminescence peut être fortement modulée par l'application d'un champ magnétique.

La transition non radiative entre les états 3E et 1E est plus probable pour niveaux d'énergie de spin ms = ±1 que pour les niveaux de spin ms = 0. En utilisant une fréquence plus élevée que toutes les transitions (typiquement 2,32 eV, soit 532 nm), il est ainsi possible de pomper les électrons sur les niveaux de spin ms = ±1 de l'état 3A vers l'état 3E, d'où ils ont une probabilité élevée de passer à l'état 1E par transition non radiative, et de là retourner à l'état fondamental sur un niveau de spin ms = 0, tandis que les électrons sur un niveau de spin ms = 0 passent de l'état 3A à 3E avant de retourner à l'état 3A avec une faible probabilité de passer par l'état 1E. Il s'ensuit que, après un nombre suffisant de tels cycles, l'état du centre NV finit par se confondre avec les niveaux de spin ms = 0. Cette propriété peut être mise à profit pour initialiser l'état quantique du centre NV dans le cadre d'un système de traitement d'information quantique.

L'état excité 3E présente un niveau supplémentaire de séparation des niveaux d'énergie en raison de la dégénérescence des orbitales et de l'interaction spin-orbite. Il est possible de moduler cette séparation des niveaux d'énergie en appliquant un champ électrique statique[14],[20] de la même manière que le champ magnétique décrit plus haut, bien que la physique sous-jacente soit dans ce cas plus complexe. Il est ainsi possible de moduler l'intensité et la position des raies de luminescence en appliquant au cristal un champ magnétique ou un champ électrique. En outre, la différence d'énergie entre les niveaux de spin ms = 0 et ms = ±1 correspond à la région des micro-ondes, de sorte qu'on peut modifier la population de ces niveaux d'énergie en irradiant les centres NV avec des micro-ondes, et donc ainsi moduler l'intensité de la luminescence des centres NV irradiés.

Les niveaux d'énergie des électrons de spin ms = ±1 présentent une division supplémentaire due à leur structure hyperfine, de sorte que l'absorption optique et la luminescence d'un centre NV− consiste en une douzaine de raies étroites avec une séparation dans le domaine du mégahertz-gigahertz. Toutes ces raies peuvent être résolues, et leur position et leur intensité peuvent être modulées à l'aide des outils suivants :

  1. l'amplitude et l'orientation d'un champ magnétique, qui sépare les niveaux d'énergie des électrons de spin ms = ±1 dans les états fondamental et excité ;
  2. l'amplitude et l'orientation d'une déformation du réseau, qui peut être appliquée par exemple en comprimant le diamant. Un effet semblable peut être obtenu en appliquant un champ électrique[14],[20], lequel peut être contrôlé avec une précision bien meilleure.
  3. l'irradiation micro-onde continue, qui modifie la population des niveaux d'énergie à l'état fondamental et à l'état excité[20] ;
  4. l'irradiation par un laser réglable, susceptible d'exciter certains sous-niveaux d'énergie de l'état fondamental et de l'état excité[20],[21] ;
  5. outre ces stimuli statiques, il est possible d'exploiter divers effets dynamiques (écho de spin (en), oscillations de Rabi, etc.) en appliquant une séquence très précise d'impulsions micro-onde[22],[23],[24],[25],[26]. La première impulsion excite les spins des électrons de manière cohérente, et c'est sur cette cohérence qu'on agit ensuite avec les impulsions suivantes. Ces effets dynamiques sont importants pour la réalisation d'ordinateurs quantiques, qui sont supposés devoir travailler à fréquence élevée. En manipulant la population, il est possible de faire passer le centre NV dans un état plus sensible ou plus stable[27],[28].

Il convient de remarquer la structure des niveaux d'énergie décrite ci-dessus n'a rien d'exceptionnel pour un défaut cristallin dans le diamant ou dans d'autres semiconducteurs[29] ; c'est en fait la combinaison d'un ensemble de facteurs favorables (connaissances antérieures, facilité de production et d'excitation, etc.), davantage que cette structure seule, qui a conduit à choisir les centres NV− pour ces recherches.

Dynamique des spins
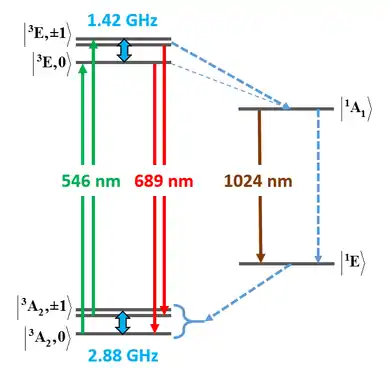
Représentation de la dynamique des spins dans un centre NV− du diamant. La transition principale entre les états triplet fondamental et excité conserve le spin dans la plupart des cas. La relaxation à travers l'état singulet intermédiaire conduit à une polarisation de spin en favorisant les transitions des niveaux ms = ±1 vers les niveaux de spin ms = 0. Les longueurs d'onde d'absorption et d'émission sont indiquées toutes les deux[30] car elles diffèrent en raison du déplacement de Stokes[31].
Erratum : la transition de l'état |1A1⟩ vers |1E⟩ est à 1 042 nm[32].

En considérant le centre NV− comme un système à plusieurs électrons, il est possible de le représenter par le diagramme ci-dessus, dans lequel les états sont indiqués par leur symétrie avec un exposant gauche valant 3 pour indiquer un état triplet (S = 1) et valant 1 pour indiquer un état singulet (S = 0). Il est bien admis aujourd'hui qu'on est en présence de deux états triplet et de deux états singulet intermédiaires[33].

L'excitation optique conserve le spin, mais il existe une probabilité élevée que les états |3E,±1⟩ se relaxent de manière non radiative vers l'état singulet |1A1⟩. Ceci se produit à une vitesse significative car la courbe d'énergie en fonction de la position des atomes à l'état |3E,±1⟩ croise celle de l'état |1A1⟩, de sorte que, pendant les quelques instants de relaxation vibratoire de l'ion suivant son excitation, il est possible que le spin change sans que cette transition nécessite beaucoup d'énergie[34]. Il est important de remarquer que ce mécanisme peut également conduire à une transition de |3E,0⟩ vers |1A1⟩, mais la vitesse de ce croisement inter-systèmes est bien plus faible que celle depuis les états |3E,±1⟩, raison pour laquelle cette transition est représentée par un trait fin dans le diagramme ci-dessus. Ce dernier représente également les chemins de relaxation non radiative et infrarouge entre les deux états singulet, et la structure fine des niveaux d'énergie des états triplet, dont les différences correspondent aux fréquences micro-ondes.

Certains auteurs expliquent la dynamique du centre NV− en considérant que la transition de |1E⟩ vers |3A2,±1⟩ est faible, mais, comme l'ont montré Robledo et al.[35], le seul fait que la probabilité de transition vers |1A1⟩ est plus faible pour |3E,0⟩ que pour |3E,±1⟩ suffit à polariser le spin vers ms = 0.

Applications et recherches
Microscopie thermique à balayage (en) à l'aide de centres NV.
(a) Schéma du montage de l'expérience. Un courant électrique est appliqué sur les broches d'un cantilever en silicium dopé au phosphore (P:Si) d'un microscope à force atomique et chauffe la section terminale au-dessus de la pointe en silicium intrinsèque (i-Si). La lentille inférieure excite un nanocristal de diamant avec une lumière laser verte et capte la photoluminescence (PL) du cristal. Celui-ci contient un centre NV et est fixé sur la pointe du microscope. Un fil sur la surface de l'échantillon sert de source de rayonnement micro-onde (mw). La température Th du cantilever est déterminée à partir du courant et de la tension du dispositif.
(b) Spectres ODMR (en) du centre NV à trois températures différentes. La séparation des raies provient d'un champ magnétique d'environ 1 mT.
(c) Image de la conductivité thermique d'une lettre E en or sur un saphir. Les cercles blancs indiquent les formations sans corrélation avec la topographie du microscope.
(d) Image par photoluminescence du cantilever et de la pointe du microscope montrant le nancristal de diamant comme un point lumineux.
(e) Zoom sur l'image du centre NV par photoluminescence.

Les caractéristiques spectrales et l'intensité des signaux optiques des centres NV− sont sensibles aux perturbations extérieures telles que la température, les déformations du cristal et les champs magnétique et électrique. L'utilisation de la forme du spectre n'est cependant pas utilisable pour mesurer ces perturbations car il faudrait pour cela refroidir le diamant à des températures cryogéniques pour rendre plus nets les signaux des centres NV−. L'utilisation de l'intensité de la luminescence peut en revanche être utilisée de manière bien plus pratique que les caractéristiques spectrales car elle présente une résonance nette lorsqu'une micro-onde dont la longueur d'onde correspond à la séparation des niveaux d'énergie à l'état fondamental. Les signaux de résonance magnétique détectés optiquement sont nets même à température ambiante et peuvent être utilisés dans des détecteurs ou des sondes miniatures. De telles sondes peuvent détecter des champs magnétiques de quelques nanotesla[36] ou des champs électriques de l'ordre de 10 V·cm-1[37] à des fréquences de l'ordre du kilohertz après une centaine de secondes de lissage. À l'aide d'un mécanisme semblable, des centres NV− ont été utilisés en microscopie thermique à balayage (en) pour établir des cartographies spatiales à haute résolution de température et de conductivité thermique[38].

Des centres NV− peuvent également être utilisés comme détecteurs pour mesurer le tenseur des contraintes mécaniques dans le volume du cristal. Pour cette application, on utilise la séparation des raies zéro phonon induite par les contraintes, ainsi que ses propriétés de polarisation[39]. On a pu démontrer la possibilité d'utiliser ce dispositif dans des conditions extrêmes à l'aide d'un récepteur radio robuste à modulation de fréquence utilisant la photoluminescence dépendante du spin électronique qui a fonctionné jusqu'à 350 °C[40].

Outre les applications du domaine de l'optique quantique, la luminescence des centres NV− du diamant peut être appliquée pour imager des processus biologiques comme la circulation des fluides dans les cellules vivantes[41]. Cette application repose sur la bonne compatibilité des nanoparticules de diamant dans les cellules vivantes et sur les propriétés favorables de la photoluminescence des centres NV−, telles que forte intensité, facilité d'excitation et de détection, stabilité dans le temps, etc.). Contrairement aux grands monocristaux de diamant, les nanodiamants sont bon marché (de l'ordre d'un euro par gramme) et facilement disponibles sur le marché. Les centres NV− y sont produits par irradiation suivi de recuit comme décrit plus haut. Ces nanodiamants sont introduits dans les cellules et leur luminescence est suivie à l'aide d'un microscope à fluorescence[42].

Par ailleurs, les centres NV ont été étudiés comme systèmes biomimétiques pour émuler la dynamique de spin des paires de radicaux des magnétorécepteurs de certains êtres vivants[43],[44].

On a pu réaliser l'émission stimulée de centres NV− à partir de la bande satellite de phonons mais pas de la raie zéro phonon. À cette fin, le centre NV a dû être excité à une longueur d'onde supérieure à 650 nm afin de ne pas être ionisé par un rayonnement trop énergétique[45].

Le premier maser continu à température ambiante a été réalisé[46],[47] en utilisant des centres NV pompés avec un rayonnement à 532 nm maintenus dans une cavité micro-onde à fort effet Purcell ainsi qu'un champ magnétique extérieur de 4 300 G. L'oscillation du maser continu a généré un signal cohérent à environ 9,2 GHz.

Les centres NV peuvent avoir une durée de cohérence (en) de spin très longue, approchant la seconde[48],[49]. Cette propriété est intéressante pour les applications en détection quantique[50] et en communication quantique[51].

Remarques historiques

Le modèle microscopique et la plupart des propriétés optiques des ensembles de centres NV− ont été clairement établies dans les années 1970 à partir de mesures optiques combinées avec des mesures ce contraintes uniaxiales[2] et de résonance paramagnétique électronique[5],[6] (EPR). Cependant, une erreur d'interprétation des résultats de l'EPR (on pensait que l'illumination était nécessaire à l'observation des signaux EPR des centres NV−) conduisit à attribuer les multiplicités de spin aux niveaux d'énergie de manière erronée. On montra en 1991 que les signaux d'EPR pouvaient être observés dans illumination[7], ce qui permit d'établir le diagramme présenté plus haut. La séparation magnétique dans l'état excité n'a été mesurée qu'à la fin des années 2000[19].

La caractérisation de centres NV− isolés est un sujet d'actives recherches dans les années 2010. L'une des premières publications dans ce domaine remonte à 1997[8] : cet article démontrait que la fluorescence de centres NV− isolés peut être détectée à température ambiante et que ce défaut cristallin montre une parfaite photostabilité.

Notes et références
  1. (en) C. Schreyvogel, V. Polyakov, R. Wunderlich, J. Meijer et C. E. Nebel, « Active charge state control of single NV centres in diamond by in-plane Al-Schottky junctions », Scientific Reports, vol. 5,‎ , article no 12160 (PMID 26177799, PMCID 4503995, DOI 10.1038/srep12160, Bibcode 2015NatSR...512160S, lire en ligne)
  2. (en) G. Davies, M. F. Hamer et William Charles Price, « Optical studies of the 1.945 eV vibronic band in diamond », Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, vol. 348, no 1653,‎ , p. 285-298 (DOI 10.1098/rspa.1976.0039, Bibcode 1976RSPSA.348..285D, lire en ligne)
  3. (en) Yoshimi Mita, « Change of absorption spectra in type-Ib diamond with heavy neutron irradiation », Physical Review B, vol. 53, no 17,‎ , p. 11360-11364 (DOI 10.1103/PhysRevB.53.11360, Bibcode 1996PhRvB..5311360M, lire en ligne)
  4. (en) K. Iakoubovskiidag, G. J. Adriaenssensdag et M. Nesladekddag, « Photochromism of vacancy-related centres in diamond », Journal of Physics: Condensed Matter, vol. 12, no 2,‎ , p. 189-199 (DOI 10.1088/0953-8984/12/2/308, Bibcode 2000JPCM...12..189I, lire en ligne)
  5. (en) J. H. N. Loubser et J. A. van Wyk, « Electron Spin Resonance in Annealed Type 1b Diamond », Diamond Research, vol. 11, 1977, p. 4–7. (ISSN 0070-4679)
  6. (en) J. H. N. Loubser et J. A. van Wyk, « Electron spin resonance in the study of diamond », Reports on Progress in Physics, vol. 41, no 8,‎ , p. 1201-1248 (DOI 10.1088/0034-4885/41/8/002, Bibcode 1978RPPh...41.1201L, lire en ligne)
  7. (en) D. A. Redman, S. Brown, R. H. Sands et S. C. Rand, « Spin dynamics and electronic states of N-V centers in diamond by EPR and four-wave-mixing spectroscopy », Physical Review Letters, vol. 67, no 24,‎ , p. 3420-3423 (PMID 10044729, DOI 10.1103/PhysRevLett.67.3420, Bibcode 1991PhRvL..67.3420R, lire en ligne)
  8. (en) A. Gruber, A. Dräbenstedt, C. Tietz, L. Fleury, J. Wrachtrup et C. von Borczyskowski, « Scanning Confocal Optical Microscopy and Magnetic Resonance on Single Defect Centers », Science, vol. 276, no 5321,‎ , p. 2012-2014 (DOI 10.1126/science.276.5321.2012, lire en ligne)
  9. (en) S. Felton, A. M. Edmonds, M. E. Newton, P. M. Martineau, D. Fisher et D. J. Twitchen, « Electron paramagnetic resonance studies of the neutral nitrogen vacancy in diamond », Physical Review B, vol. 77, no 8,‎ , article no 081201 (DOI 10.1103/PhysRevB.77.081201, Bibcode 2008PhRvB..77h1201F, lire en ligne)
  10. (en) David D. Awschalom, Ryan Epstein et Ronald Hanson, « The Diamond Age of Spintronics », Scientific American, vol. 297, no 4,‎ , p. 84-91 (PMID 17926759, DOI 10.1038/scientificamerican1007-84, JSTOR 26069461, Bibcode 2007SciAm.297d..84A, lire en ligne)
  11. (en) A. R. Lang, M. Moore, A. P. W. Makepeace, W. Wierzchowski, C. M. Welbourn et F. T. Smith, « On the dilatation of synthetic type Ib diamond by substitutional nitrogen impurity », Philosophical Transactions of the Royal Society A, vol. 337, no 1648,‎ , p. 497-520 (DOI 10.1098/rsta.1991.0135, Bibcode 1991RSPTA.337..497L, lire en ligne)
  12. (en) Konstantin Iakoubovskii et Guy J. Adriaenssens, « Trapping of vacancies by defects in diamond », Journal of Physics: Condensed Matter, vol. 13, no 26,‎ , article no 6015 (DOI 10.1088/0953-8984/13/26/316, Bibcode 2001JPCM...13.6015I, lire en ligne)
  13. (en) A. M. Edmonds, U. F. S. D’Haenens-Johansson, R. J. Cruddace, M. E. Newton, K.-M. C. Fu, C. Santori, R. G. Beausoleil, D. J. Twitchen et M. L. Markham, « Production of oriented nitrogen-vacancy color centers in synthetic diamond », Physical Review B, vol. 86, no 3,‎ , article no 035201 (DOI 10.1103/PhysRevB.86.035201, Bibcode 2012PhRvB..86c5201E, lire en ligne)
  14. (en) Ph. Tamarat, T. Gaebel, J. R. Rabeau, M. Khan, A. D. Greentree, H. Wilson, L. C. L. Hollenberg, S. Prawer, P. Hemmer, F. Jelezko et J. Wrachtrup, « Stark Shift Control of Single Optical Centers in Diamond », Physical Review Letters, vol. 97, no 8,‎ , article no 083002 (PMID 17026299, DOI 10.1103/PhysRevLett.97.083002, Bibcode 2006PhRvL..97h3002T, arXiv 0607170, lire en ligne)
  15. (en) S. Kühn, C. Hettich, C. Schmitt, J‐PH. Poizat et V. Sandoghdar, « Diamond colour centres as a nanoscopic light source for scanning near‐field optical microscopy », Journal of Microscopy, vol. 202, no 1,‎ , p. 2-6 (PMID 11298860, DOI 10.1046/j.1365-2818.2001.00829.x, lire en ligne)
  16. (en) F. De Weerdt, A. T. Collins, M. Zugik et A. Connor, « Sub-threshold excitation of luminescence of defects in diamond », Journal of Physics: Condensed Matter, vol. 17, no 50,‎ , article no 8005 (DOI 10.1088/0953-8984/17/50/018, Bibcode 2005JPCM...17.8005D, lire en ligne)
  17. (en) A. T. Collins, M. F. Thomaz et M. I. B. Jorge, « Luminescence decay time of the 1.945 eV centre in type Ib diamond », Journal of Physics C: Solid State Physics, vol. 16, no 11,‎ , article no 2177 (DOI 10.1088/0022-3719/16/11/020, lire en ligne)
  18. (en) H. Hanzawa, Y. Nisida et T. Kato, « Measurement of decay time for the NV centre in Ib diamond with a picosecond laser pulse », Diamond and Related Materials, vol. 6, no 11,‎ , p. 1595-1598 (DOI 10.1016/S0925-9635(97)00037-X, lire en ligne)
  19. (en) G. D. Fuchs, V. V. Dobrovitski, R. Hanson, A. Batra, C. D. Weis, T. Schenkel et D. D. Awschalom, « Excited-State Spectroscopy Using Single Spin Manipulation in Diamond », Physical Review Letters, vol. 101, no 11,‎ , article no 117601 (PMID 18851332, DOI 10.1103/PhysRevLett.101.117601, Bibcode 2008PhRvL.101k7601F, lire en ligne)
  20. (en) Ph. Tamarat, N. B. Manson, J. P. Harrison, R. L. McMurtrie, A. Nizovtsev, C. Santori, R. G. Beausoleil, P. Neumann, T. Gaebel, F. Jelezko, P. Hemmer et J. Wrachtrup, « Spin-flip and spin-conserving optical transitions of the nitrogen-vacancy centre in diamond », New Journal of Physics, vol. 10, no 4,‎ , article no 045004 (DOI 10.1088/1367-2630/10/4/045004, Bibcode 2008NJPh...10d5004T, lire en ligne)
  21. (en) Charles Santori, Philippe Tamarat, Philipp Neumann, Jörg Wrachtrup, David Fattal, Raymond G. Beausoleil, James Rabeau, Paolo Olivero, Andrew D. Greentree, Steven Prawer, Fedor Jelezko et Philip Hemmer, « Coherent Population Trapping of Single Spins in Diamond under Optical Excitation », Physical Review Letters, vol. 97, no 24,‎ , article no 247401 (PMID 17280321, DOI 10.1103/PhysRevLett.97.247401, Bibcode 2006PhRvL..97x7401S, arXiv 0607147, lire en ligne)
  22. (en) R. Hanson, O. Gywat et D. D. Awschalom, « Room-temperature manipulation and decoherence of a single spin in diamond », Physical Review B, vol. 74, no 16,‎ , article no 161203 (DOI 10.1103/PhysRevB.74.161203, Bibcode 2006PhRvB..74p1203H, arXiv 0608233, lire en ligne)
  23. (en) M. V. Gurudev Dutt, L. Childress, L. Jiang, E. Togan, J. Maze, F. Jelezko, A. S. Zibrov, P. R. Hemmer et M. D. Lukin, « Quantum Register Based on Individual Electronic and Nuclear Spin Qubits in Diamond », Science, vol. 316, no 5829,‎ , p. 1312-1316 (PMID 17540898, DOI 10.1126/science.1139831, Bibcode 2007Sci...316.....D, lire en ligne)
  24. (en) L. Childress, M. V. Gurudev Dutt, J. M. Taylor, A. S. Zibrov, F. Jelezko, J. Wrachtrup, P. R. Hemmer et M. D. Lukin, « Coherent Dynamics of Coupled Electron and Nuclear Spin Qubits in Diamond », Science, vol. 314, no 5797,‎ , p. 281-285 (PMID 16973839, DOI 10.1126/science.1131871, Bibcode 2006Sci...314..281C, lire en ligne)
  25. (en) A. Batalov, C. Zierl, T. Gaebel, P. Neumann, I.-Y. Chan, G. Balasubramanian, P. R. Hemmer, F. Jelezko et J. Wrachtrup,, « Temporal Coherence of Photons Emitted by Single Nitrogen-Vacancy Defect Centers in Diamond Using Optical Rabi-Oscillations », Physical Review Letters, vol. 100, no 7,‎ , article no 077401 (PMID 18352594, DOI 10.1103/PhysRevLett.100.077401, Bibcode 2008PhRvL.100g7401B, lire en ligne)
  26. (en) F. Jelezko, T. Gaebel, I. Popa, A. Gruber et J. Wrachtrup, « Observation of Coherent Oscillations in a Single Electron Spin », Physical Review Letters, vol. 92, no 7,‎ , article no 076401 (PMID 14995873, DOI 10.1103/PhysRevLett.92.076401, Bibcode 2004PhRvL..92g6401J, lire en ligne)
  27. (en) J. R. Maze, P. L. Stanwix, J. S. Hodges, S. Hong, J. M. Taylor, P. Cappellaro, L. Jiang, M. V. Gurudev Dutt, E. Togan, A. S. Zibrov et A. Yacoby, « Nanoscale magnetic sensing with an individual electronic spin in diamond », Nature, vol. 455, no 7213,‎ , p. 644–647 (ISSN 0028-0836, PMID 18833275, DOI 10.1038/nature07279, lire en ligne)
  28. (en) C. L. Degen, F. Reinhard et P. Cappellaro, « Quantum sensing », Reviews of Modern Physics, vol. 89, no 3,‎ , p. 035002 (ISSN 0034-6861, DOI 10.1103/RevModPhys.89.035002, lire en ligne)
  29. (en) Igor Aharonovich, Chunyuan Zhou, Alastair Stacey, Julius Orwa, Stefania Castelletto, David Simpson, Andrew D. Greentree, François Treussart, Jean-Francois Roch et Steven Prawer, « Enhanced single-photon emission in the near infrared from a diamond color center », Physical Review B, vol. 79, no 23,‎ , article no 235316 (DOI 10.1103/PhysRevB.79.235316, Bibcode 2009PhRvB..79w5316A, lire en ligne)
  30. (en) Luke Gordon, Justin R. Weber, Joel B. Varley, Anderson Janotti, David D. Awschalom et Chris G. Van de Walle, « Quantum computing with defects », Proceedings of the National Academy of Sciences of the United States of America, vol. 107, no 19,‎ , p. 8513-8518 (PMID 20404195, PMCID 2889300, DOI 10.1073/pnas.1003052107, JSTOR 25681448, Bibcode 2010PNAS..107.8513W, arXiv 1003.1754, lire en ligne)
  31. (en) L. J. Rogers, M. W. Doherty, M. S. J. Barson, S. Onoda, T. Ohshima et N. B. Manson, « Singlet levels of the NV− centre in diamond », New Journal of Physics, vol. 17, no 1,‎ , article no 013048 (DOI 10.1088/1367-2630/17/1/013048, Bibcode 2015NJPh...17a3048R, arXiv 1407.6244, lire en ligne)
  32. (en) L. J. Rogers, S. Armstrong, M. J. Sellars et N. B. Manson, « Infrared emission of the NV centre in diamond: Zeeman and uniaxial stress studies », New Journal of Physics, vol. 10, no 10,‎ , article no 103024 (DOI 10.1088/1367-2630/10/10/103024, Bibcode 2008NJPh...10j3024R, arXiv 0806.0895, lire en ligne)
  33. (en) Marcus W. Doherty, Neil B. Manson, Paul Delaney, Fedor Jelezko, Jörg Wrachtrup et Lloyd C. L. Hollenberg, « The nitrogen-vacancy colour centre in diamond », Physics Reports, vol. 528, no 1,‎ , p. 1-45 (DOI 10.1016/j.physrep.2013.02.001, Bibcode 2013PhR...528....1D, lire en ligne)
  34. (en) SangKook Choi, Manish Jain et Steven G. Louie, « Mechanism for optical initialization of spin in NV− center in diamond », Physical Review B, vol. 86, no 4,‎ , article no 041202 (DOI 10.1103/PhysRevB.86.041202, Bibcode 2012PhRvB..86d1202C, lire en ligne)
  35. (en) Lucio Robledo, Hannes Bernien, Toeno van der Sar et Ronald Hanson, « Spin dynamics in the optical cycle of single nitrogen-vacancy centres in diamond », New Journal of Physics, vol. 13, no 2,‎ , article no 025013 (DOI 10.1088/1367-2630/13/2/025013, Bibcode 2011NJPh...13b5013R, arXiv 1010.1192, lire en ligne)
  36. (en) J. R. Maze, P. L. Stanwix, J. S. Hodges, S. Hong, J. M. Taylor, P. Cappellaro, L. Jiang, M. V. Gurudev Dutt, E. Togan, A. S. Zibrov, A. Yacoby, R. L. Walsworth et M. D. Lukin, « Nanoscale magnetic sensing with an individual electronic spin in diamond », Nature, vol. 455, no 7213,‎ , p. 644-647 (PMID 18833275, DOI 10.1038/nature07279, Bibcode 2008Natur.455..644M, lire en ligne)
  37. (en) F. Dolde, H. Fedder, M. W. Doherty, T. Nöbauer, F. Rempp, G. Balasubramanian, T. Wolf, F. Reinhard, L. C. L. Hollenberg, F. Jelezko et J. Wrachtrup, « Electric-field sensing using single diamond spins », Nature Physics, vol. 7, no 6,‎ , p. 459-463 (DOI 10.1038/nphys1969, Bibcode 2011NatPh...7..459D, lire en ligne)
  38. (en) Abdelghani Laraoui, Halley Aycock-Rizzo, Yang Gao, Xi Lu, Elisa Riedo et Carlos A. Meriles, « Imaging thermal conductivity with nanoscale resolution using a scanning spin probe », Nature communications, vol. 6,‎ , article no 8954 (PMID 26584676, PMCID 4673876, DOI 10.1038/ncomms9954, Bibcode 2015NatCo...6E8954L, arXiv 1511.06916, lire en ligne)
  39. (en) Fabio Grazioso, Brian R. Patton, Paul Delaney, Matthew L. Markham, Daniel J. Twitchen et Jason M. Smith, « Measurement of the full stress tensor in a crystal using photoluminescence from point defects: The example of nitrogen vacancy centers in diamond », Applied Physics Letters, vol. 103, no 10,‎ , article no 101905 (DOI 10.1063/1.4819834, Bibcode 2013ApPhL.103j1905G, arXiv 1110.3658, lire en ligne)
  40. (en) Linbo Shao, Mian Zhang, Matthew Markham, Andrew M. Edmonds et Marko Lončar, « Diamond Radio Receiver: Nitrogen-Vacancy Centers as Fluorescent Transducers of Microwave Signals », Physical Review Applied, vol. 6, no 6,‎ , article no 064008 (DOI 10.1103/PhysRevApplied.6.064008, Bibcode 2016PhRvP...6f4008S, lire en ligne)
  41. (en) Yi-Ren Chang, Hsu-Yang Lee, Kowa Chen, Chun-Chieh Chang, Dung-Sheng Tsai, Chi-Cheng Fu, Tsong-Shin Lim, Yan-Kai Tzeng, Chia-Yi Fang, Chau-Chung Han, Huan-Cheng Chang et Wunshain Fann, « Mass production and dynamic imaging of fluorescent nanodiamonds », Nature Nanotechnology, vol. 3, no 5,‎ , p. 284-288 (PMID 18654525, DOI 10.1038/nnano.2008.99, lire en ligne)
  42. (en) Igor Aharonovich, Andrew D. Greentree et Steven Prawer, « Diamond photonics », Nature Photonics, vol. 5, no 7,‎ , p. 397-405 (DOI 10.1038/nphoton.2011.54, Bibcode 2011NaPho...5..397A, lire en ligne)
  43. (en) « Cryptochrome and Magnetic Sensing », sur http://www.ks.uiuc.edu/, Université de l'Illinois à Urbana-Champaign (consulté le ).
  44. (en) Jianming Cai, Gian Giacomo Guerreschi et Hans J. Briegel, « Quantum Control and Entanglement in a Chemical Compass », Physical Review Letters, vol. 104, no 22,‎ , article no 220502 (PMID 20867156, DOI 10.1103/PhysRevLett.104.220502, Bibcode 2010PhRvL.104v0502C, arXiv 0906.2383, lire en ligne)
  45. (en) Jan Jeske, Desmond W. M. Lau, Xavier Vidal, Liam P. McGuinness, Philipp Reineck, Brett C. Johnson, Marcus W. Doherty, Jeffrey C. McCallum, Shinobu Onoda, Fedor Jelezko, Takeshi Ohshima, Thomas Volz, Jared H. Cole, Brant C. Gibson et Andrew D. Greentree, « Stimulated emission from nitrogen-vacancy centres in diamond », Nature Communications, vol. 8,‎ , article no 14000 (PMID 28128228, PMCID 5290152, DOI 10.1038/ncomms14000, Bibcode 2017NatCo...814000J, arXiv 1602.07418, lire en ligne)
  46. (en) Jonathan D. Breeze, Enrico Salvadori, Juna Sathian, Neil McN. Alford et Christopher W. M. Kay, « Continuous-wave room-temperature diamond maser », Nature, vol. 555, no 7697,‎ , p. 493-496 (PMID 29565362, DOI 10.1038/nature25970, Bibcode 2018Natur.555..493B, arXiv 1710.07726, lire en ligne)
  47. (en) Ren-Bao Liu, « A diamond age of masers », Nature, vol. 555, no 7697,‎ , p. 447-449 (PMID 29565370, DOI 10.1038/d41586-018-03215-3, Bibcode 2018Natur.555..447L, lire en ligne)
  48. (en) P. C. Maurer, G. Kucsko, C. Latta, L. Jiang, N. Y. Yao, S. D. Bennett, F. Pastawski, D. Hunger, N. Chisholm, M. Markham, D. J. Twitchen, J. I. Cirac et M. D. Lukin, « Room-Temperature Quantum Bit Memory Exceeding One Second », Science, vol. 336, no 6086,‎ , p. 1283-1286 (PMID 22679092, DOI 10.1126/science.1220513, Bibcode 2012Sci...336.1283M, lire en ligne)
  49. (en) N. Bar-Gill, L.M. Pham, A. Jarmola, D. Budker et R.L. Walsworth, « Solid-state electronic spin coherence time approaching one second », Nature Communications, vol. 4,‎ , article no 1743 (PMID 23612284, DOI 10.1038/ncomms2771, Bibcode 2013NatCo...4E1743B, arXiv 1211.7094, lire en ligne)
  50. (en) H. J. Mamin, M. Kim, M. H. Sherwood, C. T. Rettner, K. Ohno, D. D. Awschalom et D. Rugar, « Nanoscale Nuclear Magnetic Resonance with a Nitrogen-Vacancy Spin Sensor », Science, vol. 339, no 6119,‎ , p. 557-560 (PMID 23372008, DOI 10.1126/science.1231540, Bibcode 2013Sci...339..557M, lire en ligne)
  51. (en) B. Hensen, H. Bernien, A. E. Dréau, A. Reiserer, N. Kalb, M. S. Blok, J. Ruitenberg, R. F. L. Vermeulen, R. N. Schouten, C. Abellán, W. Amaya, V. Pruneri, M. W. Mitchell, M. Markham, D. J. Twitchen, D. Elkouss, S. Wehner, T. H. Taminiau et R. Hanson, « Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres », Nature, vol. 526, no 7575,‎ , p. 682-686 (PMID 26503041, DOI 10.1038/nature15759, Bibcode 2015Natur.526..682H, arXiv 1508.05949, lire en ligne)
  • Portail des sciences des matériaux
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.