Cercle de Lemoine

Les parallèles aux côtés d'un triangle menées par le point de Lemoine coupent les côtés en six points cocycliques.

Le centre du cercle est le milieu du diamètre de Brocard [OL] où O est le centre du cercle circonscrit. Ce point a pour nombre de Kimberling X₁₈₂ . Le premier cercle de Lemoine est donc concentrique avec le cercle de Brocard.

Le rayon du premier cercle de Lemoine, avec les longueurs a = BC, b = AC et c = AB, R le rayon du cercle circonscrit à ABC, et ω l'angle de Brocard du triangle de référence vaut :

${\displaystyle R_{L}={\frac {1}{2}}R\sec(\omega )={\frac {abc{\sqrt {a^{2}b^{2}+b^{2}c^{2}+c^{2}a^{2}}}}{(a^{2}+b^{2}+c^{2}){\sqrt {(a+b+c)(a+b-c)(b+c-a)(c+a-b)}}}}.}$

Les droites (RQ), (ST) et (PU) sont antiparallèles aux côtés d'un triangle. Les segments sont de même longueur et leurs milieux A’, B’ et C’ situés sur les symédianes forment un triangle A’B’C’ homothétique de ABC dans une homothétie de centre L.

L'hexagone PQRSTU est un hexagone de Lemoine.

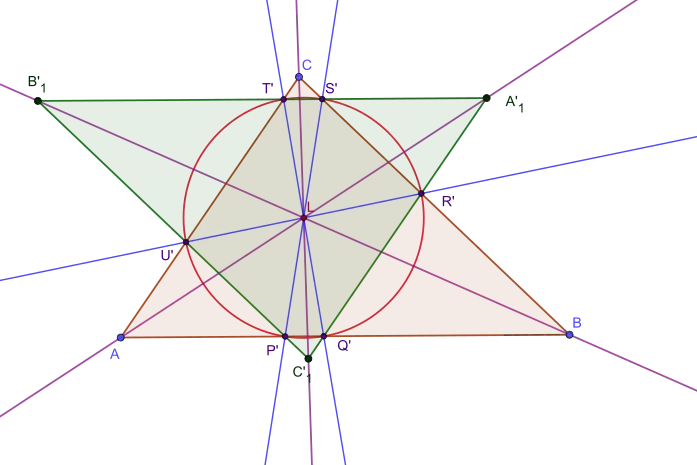
Les antiparallèles aux côtés d'un triangle ABC, menées par le point de Lemoine L, coupent les côtés du triangle en six points cocycliques.

Ces points sont situés sur le deuxième cercle de Lemoine centré en L et, en notant les longueurs des côtés de rayon r_K = ^abc⁄_{(a² + b² + c²)}.

Ce cercle est également appelé cercle des cosinus, car les longueurs des cordes [P'Q'], [R'S'] et [T'U'] sont proportionnelles aux cosinus des angles aux sommets opposés du triangle ABC.

Les points d'intersection A’₁, B’₁, C’₁ des droites (RQ), (ST) et (PU) sont situés sur les symédianes.

Ils forment un triangle A’₁B’₁C’₁ symétrique de ABC dans une symétrie de centre L. Par la même symétrie, les triangles P'R'T' et Q'S'U' sont symétriques.

Les quadrilatères P'Q'S'T', Q'R'T'U' et R'S'U'P' sont des rectangles.

• (en) Eric W. Weisstein, « First Lemoine Circle », sur MathWorld
• (en) Eric W. Weisstein, « Cosine Circle », sur MathWorld

• Portail de la géométrie