Champ magnétique planétaire

Plusieurs planètes ou autres corps membres d'un système planétaire sont connus pour posséder, ou avoir possédé, un champ magnétique.

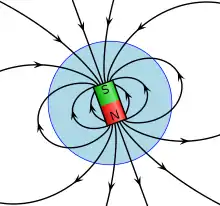
Le champ magnétique d'une planète ressemble à celui d'un aimant droit, incliné par rapport à l'axe de rotation

Historique

La Boussole est connue en Chine depuis l'antiquité (la date précise de son invention reste inconnue) et introduite (ou réinventée) en Europe et au Moyen-orient vers 1200. Aucune théorie explicative n'existe alors sur son fonctionnement : les sources médiévales se contentent de constater que la boussole indique toujours la direction de l'étoile polaire[1].

En 1600, la notion de champ magnétique terrestre fait ses premiers pas avec William Gilbert, qui réalise une maquette appelée Terrella, qui est une sphère aimantée. Il montre qu'une boussole placée sur la terrella indique toujours le même point. Il a ainsi compris que la terre possède un champ magnétique global[2]. Pour l'expliquer, il propose que l'ensemble de la planète possède une aimantation permanente, similaire à celle d'un minéral comme la magnétite[3]. En réalité, l'aimantation permanente de minéraux ne peut expliquer le champ magnétique à l'échelle d'une planète : les minéraux aimantables sont plutôt rares, et ne gardent leur cohérence qu'à des températures modestes (sous leur température de Curie), donc seulement près de la surface d'une planète comme la Terre[4].

Modèle de la dynamo planétaire

Schéma des courants convectifs d'une dynamo planétaire

Présentation générale

Le modèle dynamo, actuellement admis, a été développé par Walter M. Elsasser.

Il attribue la génération du champ magnétique à des mouvements de fluides conducteurs : il s'agit de la partie liquide du noyau ferreux (noyau externe) pour les planètes telluriques, et de l'hydrogène métallique dans le cas des planètes gazeuses[4]. Le champ magnétique d'une planète est un phénomène auto-entretenu : ainsi, de façon contre-intuitive, il est nécessaire de le prendre en compte pour comprendre les phénomènes qui lui donnent naissance[5].

Ces fluides conducteurs sont soumis à plusieurs effets[4] :

des effets de convection thermique, correspondance à un transport de chaleur vers l'extérieur ;
des effets de convection chimique (différence de composition) peuvent s'y ajouter ;
la force de Coriolis due à la rotation de la planète, tend à faire tourbillonner leur mouvement ;
l’apparition d'une force électromotrice, car il se déplace dans le champ magnétique (induction). Il est donc siège d'un courant électrique ;
en conséquence, il subit aussi des forces de Lorentz.

Un équilibre dynamique s’établit entre ces différentes forces, ce qui se traduit par des courants hélicoïdaux[4]. Les courants induits entretiennent le champ magnétique.

Equations principales

L'écoulement est représenté par une équation de Navier Stokes à laquelle s'ajoute le terme de la force de Laplace [6] :

${\frac {\delta {\vec {v}}}{\delta t}}+{\vec {v}}\cdot {\vec {\Delta }}{\vec {v}}=-{\frac {1}{\rho }}{\vec {\Delta }}P+\nu \Delta {\vec {v}}+{\vec {j}}\wedge {\vec {B}}+{\vec {f}}$

Où :

${\vec {v}}$ est la vitesse.
$P$ est le tenseur des contraintes.
$vec{B}$ est le champ magnétique.

Le champ magnétique étant pour sa part commandé par l'équation :

${\frac {\delta {\vec {B}}}{\delta t}}={\frac {1}{\mu _{0}\sigma }}\nabla ^{2}{\vec {B}}+\Delta \times \left({\vec {v}}\times {\vec {B}}\right)$

Critères

La théorie du modèle dynamo et la comparaison des planètes (et principales lunes) du système solaire permet de définir un certain nombre de critères qui font qu'une planète possède, ou non, un champ magnétique auto-entretenu[7]. Le corps planétaire considéré doit posséder un noyau liquide (ou partiellement liquide), ce qui exclut d'emblée les corps non différenciés. Il faut aussi que le corps soit encore en train de se refroidir, ce qui produit des courants de convection.

Dans les planètes dont l'intérieur est largement refroidi, comme Mars, les courants convectifs sont arrêtés, et aucune dynamo planétaire ne peut fonctionner[4]. La présence d'une convection n'est cependant une condition suffisante. Les conditions pour l'existence d'une « dynamo » fonctionnelle dans un corps planétaire sont exprimées par le Nombre de Reynolds magnétique, une valeur minimale, probablement située entre 10 et 100, est nécessaire.

Un système complexe et chaotique

Une dynamo planétaire est un processus physique qui reste extrêmement difficile à modéliser. Il n'existe pas, en 2021, de modèle numérique complètement prédictif du fonctionnement de la « dynamo » d'un corps planétaire. D'une part, c'est un problème multiphysique, qui fait intervenir des équations relevant aussi bien de la mécanique des fluides que de l'électromagnétisme. En outre, les données sur le noyau terrestre (et a fortiori sur celui des autres planètes) restent fragmentaires : il n'existe aucun moyen d'observation directe, tout ce qui est connu du noyau terrestre est inféré des informations magnétiques, sismiques et gravimétriques[8].

Une dynamo planétaire est un système chaotique, où de petites perturbations peuvent aboutir à des basculements majeurs. L'illustration la plus flagrante en est le phénomène d'inversion. Le champ magnétique terrestre s'inverse de façon récurrente : au moins 40 fois au cours des dix derniers millions d'années, mais à des intervalles de temps très irréguliers[9]. Il s'agit d'un phénomène chaotique, où les deux positions extrêmes de l'axe magnétique de la Terre (aligné dans un sens ou dans l'autre sur l'axe de rotation) représentent des attracteurs[10].

Modèles comportementaux

Étant donné l'extrême complexité physique d'une dynamo planétaire, des modèles comportementaux ont été élaborés, suffisamment simples pour être mis complètement en équation ou testés en laboratoire, et capables de rendre compte de certains comportements d'une dynamo planétaire.

Bullard

Dynamo homopolaire de Bullard.

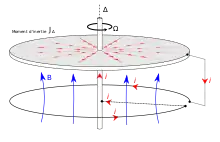
La dynamo homopolaire a été introduite par Edward Bullard, géophysicien britannique, dans les années 1950. Il s'agit d'une variante du disque de Faraday, qui, au lieu d'être placé dans l'entrefer d'un aimant permanent, est connecté en série avec une boucle qui lui est coaxiale. La mise en équation qui suit est proposée par Moffatt, qui suggère de considérer un disque segmenté pour que le courant ne puisse circuler que dans la direction radiale[11]. Le flux à travers le disque s'écrit, en adoptant un système de coordonnées cylindriques ( $z = 0$ sur le disque) :

\Phi (t)=\iint _{S}B_{z}(r,\theta ,0,t)\,r\,\mathrm {d} r\,\mathrm {d} \theta

Le champ électrique induit sur un point du disque à une distance r de l'axe est :

{\mathcal {E}}(r)=2\pi \,\Omega \,r\,B_{z}

Où $\Omega$ est la vitesse de rotation (radian/sec).

La différence de potentiel entre le moyeu et la périphérie du disque (force électromotrice) s'écrit en intégrant le terme ci-dessus le long d'un rayon. Le résultat se simplifie en :

e=\Omega \,\Phi

On introduit les termes électriques $R$ (la résistance du circuit), $L$ (son inductance) et $M$ (l'inductance mutuelle entre la boucle de courant et le disque de Faraday) :

L{\frac {\mathrm {d} i}{\mathrm {d} t}}+R\,i=M\,\Omega \,i

Bien entendu, le courant existant dans le disque soumis à un champ magnétique donne lieu à une force de Lorenz, laquelle exerce un couple qui, selon le signe, va l’accélérer ou le freiner[12]. Ce couple s'écrit :

\Gamma =i\,\Phi

On a donc, en introduisant un terme d'amortissement mécanique linéaire $\alpha$ :

J_{\Delta }{\frac {\mathrm {d} \Omega }{\mathrm {d} t}}=-\alpha \,\Omega +i\,\Phi

Ce modèle simple permet déjà de rendre compte de certains comportement comme le caractère auto-entretenu du champ magnétique, la non-linéarité, et l'existence d'hystérésis, de bifurcations et de seuils. Un premier cas de figure est de considérer le disque tournant à une vitesse Ω constante, entraîné par un moteur externe. Tant que i et B sont nuls, le système est purement mécanique. Si une perturbation crée un courant (un champ) infinitésimal, deux cas sont possibles. Si le système est trop résistif ( $R>\Omega M$ ), le courant sera évanescent. À l'inverse, si $R<\Omega M$ , le courant va être amplifié et augmenter « à l'infini », dans la limite bien sûr du couple que peut fournir le moteur externe. On a donc ici une génératrice[11]^,[12].

Rikitake

Modèle de Rikitake.

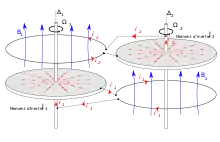
Le modèle de Rikitake revient à coupler deux dynamos de Bullard, chacune exposée au champ magnétique généré par une boucle de courant reliée à l'autre en série[13]. Il a été publié en 1958 et différentes variantes ont été étudiées, en ajoutant des moteurs, des termes de dissipation, etc. Il a été utilisé pour représenter certains comportements des dynamos planétaires, mais aussi stellaires. Dans l'une de ses variations, les deux disques représentent deux composantes du champ magnétique, respectivement colinéaire et orthogonale à l'axe de rotation de la planète (ou de l'étoile)[14].

Von Kármán

Dynamo de Von Kármán.

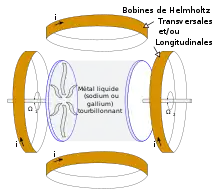
La dynamo de Von Kármán est schématisée ci-contre. Elle vise à reproduire, au laboratoire, les phénomènes propres à une dynamo planétaire. Elle utilise un volume de métal liquide (du gallium ou du sodium, liquides à des températures modérées) placé entre deux roues à palettes, qui peuvent tourner dans le même sens, ou en sens opposés, créant des mouvements tourbillonnaires. Des bobines de Helmholtz créent un champ magnétique variable (elles peuvent être placées pour qu'il soit longitudinal ou transversal) auquel le métal liquide est exposé. Ainsi, des courants induits apparaissent dans le métal, qui créent à leur tour un champ magnétique. Cette expérience a permis de reproduire le caractère auto-entretenu de la dynamo, et, surtout, fournit des données qui permettent de valider et d'améliorer les modèles numériques[15].Une itération de cette expérience, nommée VKS (Von Kármán Sodium), fonctionne depuis 2006 au Centre CEA de Cadarache[16].

Description et caractérisation du champ d'une planète

Le champ d'une planète est représenté, en première approximation, comme le champ généré par un dipôle magnétique placé au centre de la planète. Le dipôle est caractérisé par son moment dipolaire (sa valeur), et par son orientation, c'est-à-dire l'angle qu'il forme d'avec l'axe de rotation de la planète. Ces paramètres sont déterminés par problème inverse à partir de mesure de champ magnétique effectuée en surface et/ou en orbite. Ils évoluent avec le temps[17].

Pour obtenir un modèle plus fin, un quadrupôle magnétique, voir un octopôle, peuvent être ajoutés. Ils viennent corriger les différences entre les mesures et le champ dipôle qui a été déterminé[18].

Dipôle ou quadrupôle magnétique
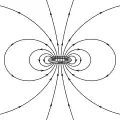Champ magnétique d'un dipôle
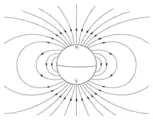Champ dipôlaire autour de la planète
Champ magnétique d'un quadrupôle

Développement en harmoniques sphériques

La développement du champ magnétique en harmoniques sphériques consiste à décomposer le potentiel scalaire du champ autour d'un objet céleste (planète ou lune) en une somme de fonctions élémentaires, un peu à la manière d'une transformation de Fourier qui décompose une fonction périodique en une somme infinie (mais dénombrable) de sinusoïdes. Le potentiel scalaire $V$ est tel que le champ magnétique ${\vec {B}}$ soit l'opposé de son gradient :

{\vec {B}}=-{\overrightarrow {\nabla }}V

.

Le potentiel magnétique n'est défini que dans un domaine simplement connexe en l'absence de courants électriques (le champ magnétique étant alors irrotationnel). Dans le cas qui nous intéresse, il est défini à l'extérieur de l'objet céleste.

Comme on s'intéresse à des objets célestes de forme sphéroïdale (en première approximation), il est naturel de travailler en coordonnées sphériques, donc d'écrire $V$ comme une fonction des coordonnées sphériques $r$ (distance au centre de l'objet), $θ$ (colatitude, l'angle au pôle) et $φ$ (longitude). On note $a$ le rayon de l'objet étudié. $V$ se décompose en deux termes pour le magnétisme dû aux sources internes (comme la dynamo active d'une planète) et aux sources externes. Sa composante interne s'écrit :

V_{\mathrm {int} }=a\sum _{n=1}^{\infty }\left({\frac {r}{a}}\right)^{1+n}T_{n}^{\mathrm {int} }

.

Pour le potentiel dû aux sources externes, son écriture est similaire, mais en puissances croissantes de $r$ :

V_{\mathrm {ext} }=a\sum _{n=1}^{\infty }\left({\frac {a}{r}}\right)^{n}T_{n}^{\mathrm {ext} }

.

Autre formes de magnétisme

Planètes telluriques du système solaire

Mercure

La champ magnétique de Mercure a été mesuré pour la première fois en 1974 par la sonde Mariner 10. Son intensité est faible : environ 1,1 % de celle du champ Terrestre. Mais sa présence constituait déjà une surprise pour les scientifiques : Mercure étant petite, il était supposé que la planète serait totalement refroidie, qu'elle n'aurait plus aucun courant de convection et donc aucun champ magnétique[19]. Les travaux plus récents confirment que le champ magnétique de Mercure est bien dû à un effet dynamo, quoique faible[20].

Vénus

Vénus ne possède aucun champ magnétique mesurable. La planète a pourtant une taille et une structure similaires à la Terre. La comparaison entre les deux planètes est donc un moyen de comprendre les mécanismes qui expliquent le champ magnétique planétaire. L'échange de chaleur convectif entre le noyau de Vénus et son manteau sont pratiquement terminés. Cela expliquerait à la fois l'absence de champ magnétique sur Vénus et son manque d'activité tectonique de 500 millions d'années[21].

Lune

Le champ magnétique actuel à la surface de la Lune est très faible (moins d'un centième du champ magnétique terrestre) et non dipolaire. Sa répartition géographique est dominée par les bassins d'impacts, les plus faibles (inférieurs à 0,2 nT) se trouvant dans les bassins les plus grands et les plus récents, Mare Orientale et Mare Imbrium, tandis que les champs les plus forts (supérieurs à 40 nT) sont mesurés au-dessus des surfaces diamétralement opposées à ces mêmes bassins[22]. Le champ magnétique lunaire est entièrement dû à la magnétisation des roches crustales, et aujourd'hui la Lune ne possède pas de champ magnétique planétaire dipolaire[23]. La magnétisation peut être due en partie à des champs magnétiques transitoires générés lors d'impacts importants, mais la majeure partie de cette magnétisation est héritée d'une époque où la Lune possédait un champ magnétique global, à l'instar de la Terre et d'autres planètes.

La présence d'un champ magnétique global peu après la formation de la Lune est attestée par l'aimantation rémanente de ses roches les plus anciennes[24]. Les études paléomagnétiques montrent qu'une dynamo lunaire a fonctionné entre au moins 4,25 et 1,92 Ga et qu'une période de champ élevé (avec une intensité moyenne du champ d'environ 77 μT en surface) a perduré entre 3,85 et 3,56 Ga, suivie d'une baisse de l'intensité de surface jusqu'en dessous de 4 μT vers 3,19 Ga[25]. La baisse d'un ordre de grandeur des paléo-intensités lunaires entre 3,56 et 3,19 Ga s'est suivie d'une période de champ bas (intensités du champ de surface de l'ordre de 5 μT) puis d'une seconde et dernière période de déclin entre 1,92 et 0,8 Ga, qui s'est terminée par l'arrêt de la dynamo lunaire, signe d'une cristallisation complète du noyau lunaire[26].

Mars

carte des anomalies magnétiques sur Mars : le champ dépasse localement le µT

Mars ne possède pas aujourd'hui de champ magnétique global. Néanmoins, certaines zones de la croûte sont aimantées et créent un champ magnétique local, à la manière des anomalies magnétiques sur Terre[27]. L'étude de ce magnétisme crustal, couplé à l'observation des traces de volcanisme a permis de déterminer que Mars a possédé, au début de son histoire, une dynamo magnétique, qui a été active pendant une durée probablement comprise entre 500 et 800 millions d'années. Ensuite, le flux de chaleur est devenu trop faible pour qu'une convection ait lieu dans le noyau ferreux[28].

Planètes géantes du système solaire

Jupiter

Aurore polaire sur Jupiter, obervée par Hubble

Jupiter possède le champ magnétique le plus puissant des planètes du Système solaire. Son moment magnétique est de 1,55 T m³, soit 20 000 fois celui de la Terre[29].

Contrairement aux autres planètes, l'existence d'un champ magnétique jovien a pu être attestée avant l'ère spatiale : en 1955, l'étude des émissions radio venant de cette planète a permis de mettre en évidence la présence d'aurores polaires, preuve indirecte de l'existence d'un champ magnétique global[30]. L'effet Zeeman, c'est-à-dire le décalage des raies spectrales sous l'effet du champ magnétique, avait aussi pu être caractérisé depuis la Terre[31].

Des mesures directes du champ jovien ont été effectuées par quatre sondes des programmes Pioneer et Voyager. La sonde Juno, qui orbite Jupiter depuis 2016 (quand les quatre sondes précédentes s'en étaient seulement approchées), a fourni des informations beaucoup plus précises. Son orbite polaire lui permet en particulier de mesurer le champ magnétique dans l'axe de la planète, ce qui est une première concernant les planètes géantes[32].

Satellites galiléens

Les satellites galiléens possèdent chacun un faible champ magnétique, qui a pu être caractérisé grâce aux survols effectués par la sonde Galileo[33]. Néanmoins, la question de savoir s'ils possèdent une dynamo active, et produisent donc leur champ magnétique de façon totalement autonome, ou si leur dipôle est induit par le champ magnétique jovien, n'est pas totalement tranchée. Concernant Io, il est très difficile de procéder à des mesures, car cette lune évolue si profondément dans le champ magnétique de Jupiter qu'il est difficile de distinguer son propre champ. Rien ne prouve la présence d'une dynamo active. Des travaux des années 2000 suggèrent que Io serait à l'équilibre thermique : la chaleur produite par les effets de marée dans son manteau serait suffisante pour que Io ne se refroidisse pas, il n'y aurait donc pas de courants de convection[34].

Europe et Callisto semblent n'avoir qu'un magnétisme induit. La meilleure explication actuelle repose sur leurs océans souterrains : l'eau liquide présente sur plusieurs kilomètres d'épaisseur serait le siège de courants induits suffisants pour expliquer leur réponse magnétique[34].

En revanche, dans le cas de Ganymède, la présence d'une dynamo active est probable, et son mécanisme principal serait la solidification du fer ou du sulfate de fer en périphérie de son noyau liquide[35].

Saturne

Le champ magnétique de Saturne est connu grâce aux sondes Pioneer 11, Voyager 1 et Voyager 2, et plus récemment Cassini[36]. Par ailleurs, des aurores polaires ont été observées depuis la Terre[37]. La dynamo de Saturne est probablement similaire, physiquement, à celle de Jupiter. Une caractéristique remarquable du champ de Saturne est qu'il est parfaitement aligné sur l'axe de rotation de la planète[34].

Titan

Du fait de sa taille, Titan a longtemps été considéré comme susceptible de posséder une dynamo active et d'avoir en conséquence son propre champ magnétique[38]. Mais la mission Cassini-Huygens a montré que non, ce qui a profondément changé la conception que les scientifiques se font de cette lune : considérée auparavant comme totalement différenciée et avec un noyau ferreux (à l'image de Ganymède), elle est vue aujourd'hui comme partiellement différenciée avec un noyau peu dense, et sans aucune convection active[39]. Il pourrait exister une réponse induite, comme dans le cas des lunes joviennes, mais elle serait très faible : le champ magnétique de Saturne étant parfaitement axisymétrique, sa variation vue par Titan au cours d'une orbite est minime[34].

Uranus et Neptune

Uranus et Neptune possèdent un champ magnétique très particulier, connu uniquement grâce aux mesures de la sonde Voyager 2, qui les a survolées respectivement en 1986 et 1989. Leur champ ne peut pas s'approcher simplement comme celui d'un dipôle. Il faut y ajouter un quadrupôle, dont la contribution en surface est aussi grande. De plus, leur axe magnétique n'est pas seulement incliné mais aussi décalé, c'est-à-dire qu'il ne passe pas par le centre de la planète[40]^,[41].

La nature inhabituelle, ni dipolaire, ni axisymétrique, du champ magnétique de ces deux planètes a pu être expliquée. Des travaux de simulation numérique ont montré qu'une telle configuration pouvait, dans des conditions bien précises, être retrouvée avec des modèles prenant en compte un effet dynamo limité à une zone assez petite autour d'un noyau fluide stable[42].

Astéroïdes

Des corps beaucoup plus petits que les planètes ou les lunes ont eu, au début de l'histoire du système solaire, un champ magnétique auto-entretenu. Des astéroïdes différentiés possédant un noyau ferreux ont connu une phase de refroidissement pendant laquelle leur noyau était partiellement liquide et sujet à des courants de convection, certains sont passés par une phase où les conditions étaient réunies pour qu'une dynamo auto-entretenue soit possible. Cette période a été très courte, comparativement à des planètes comme la Terre : les effets d'échelle sont tels qu'un corps de petite taille se refroidit bien plus rapidement. À l'échelle d'un astéroïde, les modèles suggèrent que la convection thermique est peu efficace pour actionner une dynamo et que la convection de composition est plus efficace. Elle se produit lorsque le noyau a commencé à se solidifier, du fait de la solidification du soufre, du nickel et du fer à différentes températures. Un modèle numérique concernant un astéroïde d'un diamètre de 400 km a été publié. Il montre qu'une dynamo active a pu être possible pendant cinq millions d'années, commençant 5 millions d'années après l'événement d'accrétion formant le corps considéré. Ces périodes varient selon la composition de l'objet[43]. Le champ magnétique des astéroïdes nous est connu par l'aimantation rémanente des météorites qui en proviennent. L'existence d'une aimantation rémanente dans des météorites de différents types, différenciées ou non, est connue depuis les années 1960, mais son décryptage est resté longtemps difficile[44]. Les techniques de désaimantation contrôlée s'étant depuis considérablement améliorées, des résultats concluants se sont accumulés depuis le début des années 2000. De nombreuses météorites sont porteuses d'une aimantation thermorémanente dont on peut montrer qu'elle a été acquise quand la météorite était encore au sein de son corps parent. Ces corps parents possédaient donc un champ magnétique, et d'autres astéroïdes sans doute aussi.

Météorites différenciées

Majoritairement constituées d'un métal ferromagnétique, les météorites de fer sembleraient à première vue propices à la rétention d'une aimantation thermorémanente, qui témoignerait d'un champ magnétique créé par effet dynamo dans le noyau de leurs corps parents. L'aimantation des phases principales (kamacite et taénite) est en fait trop fragile (trop sensible à toutes les perturbations subies par la météorite), d'où le fait que les météorites de fer ont fait l'objet d'assez peu d'études paléomagnétiques[45]. Il existe cependant de petites zones troubles (cloudy zones) contenant de minuscules grains de tétrataénite, à l'aimantation beaucoup plus fiable (forte coercivité). Mais les météorites de fer posent un autre problème : si elles proviennent du noyau d'un astéroïde différencié, leur température n'a dû descendre en dessous de la température de Curie qu'après la cristallisation du noyau et donc longtemps après l'arrêt de la dynamo. De fait, les zones troubles de Tazewell, une météorite du groupe IIICD, n'ont enregistré aucun champ magnétique[46]. D'autres types de météorites de fer sont plus prometteurs, notamment le groupe IIE (interprété comme provenant de poches de métal relativement superficielles) et le groupe IVA (refroidi particulièrement vite)[45].
Les pallasites (des météorites mixtes métal-silicate), au moins celles du groupe principal, ont enregistré dans leur olivine[47] et dans leurs grains de tétrataénite[48]^,[49] un champ magnétique de longue durée (jusqu'à des centaines de millions d'années après l'accrétion[48]^,[49]), attribuable à une dynamo auto-entretenue liée à la convection solutale engendrée par la cristallisation progressive du noyau de leur corps parent[49].
L'aimantation rémanente de l'eucrite ALH A81001, une achondrite basaltique formée il y a 3,69 milliards d'années, sans doute à la surface de l'astéroïde (4) Vesta, témoigne d'un champ magnétique d'au moins 2 µT à cette époque, sans doute dû à l'activité d'une dynamo dans le noyau métallique de Vesta[50].
Le corps parent des angrites (des achondrites magmatiques) possédait un champ magnétique d'au moins 10 µT entre −4 564 et −4 558 Ma, disparu avant −3 700 Ma[51]^,[52].

Météorites indifférenciées

L'une des composantes de l'aimantation rémanente de la météorite de Murchison, une chondrite carbonée du groupe CM2, a été acquise pendant ou après la formation de son corps parent, en présence d'un champ magnétique d'au moins 0,2 à 2 µT[53]. La météorite d'Allende, une chondrite carbonée du groupe CV3, porte une aimantation thermorémanente acquise dans son corps parent à la fin d'un épisode de métamorphisme, dans un champ magnétique faible (< 8 µT), sans doute moins de 40 Ma après la formation des CAI[54]. Les chondres de la météorite de Vigarano, une autre CV[55], possèdent une aimantation thermorémanente acquise probablement lors de la rupture du corps parent 9 Ma environ après la formation des CAI, quand la dynamo de cet astéroïde était encore active[56].
La météorite de Farmington, une chondrite ordinaire du groupe L5[57], possède une aimantation thermorémanente acquise dans son corps parent il y a moins de 520 Ma[58]. Les chondres de la météorite de Bjurböle, une chondrite ordinaire du groupe L/LL4[59], portent une aimantation thermorémanente qui témoigne que la dynamo du corps parent était encore active 80 à 140 Ma après le pic de son métamorphisme. La météorite de Portales Valley, une chondrite ordinaire du groupe H6, a de même enregistré un champ magnétique pendant des dizaines à des centaines d'années, environ 100 Ma après la formation du Système solaire[60].

Il semble ainsi que l'intérieur des corps parents des chondrites devait être différencié[56], au moins partiellement. Dans ce cadre, les chondrites proviendraient des couches externes de ces astéroïdes, non différenciées.

Tableau comparatif

Moment magnétique dipolaire
Astre	Moment (A m²)	Moment relatif à la Terre	Inclinaison par rapport à l'axe de rotation	Champ en surface (T), approximatif[4]	Références
Mercure	4 × 10¹⁹	0.0005		1 × 10⁻⁷	[61]
Vénus	Aucun	0	n/a	infime	[21]
Terre	7,84 × 10²²	1	11.5°	5 × 10⁻⁵	[61]
Lune	Aucun	0	n/a	Champs locaux seulement
Mars	Aucun	0	n/a	Champs locaux seulement	[27]
Jupiter	1,55 × 10²⁷	20000	10°	4 × 10⁻⁴	[61]^,[27]
Io				faible
Europe				1 × 10⁻⁷
Ganymède	1,32 × 10²⁰	0.0017	176°	2 × 10⁻⁶	[33]
Callisto				4 × 10⁻⁹
Saturne	4,6 × 10²⁵	600	<1°	5 × 10⁻⁵	[61]^,[27]
Titan				faible
Uranus	3,9 × 10²⁴	54	60°	2 × 10⁻⁵	[61]^,[27]
Neptune	2,2 × 10²⁴	30	47°	2 × 10⁻⁵	[61]^,[27]

Exoplanètes

Des preuves d'interaction magnétique entre une exoplanète et son étoile ont été obtenues pour de nombreux Jupiter chauds. En 2019, l'intensité du champ magnétique à la surface de quatre de ces Jupiter chauds a pu être mesurée : entre 20 et 120 G. C'est dix à cent fois plus que ce que prédisent les modèles de dynamo pour les planètes ayant une période de rotation de 2 à 4 jours, mais en accord avec les modèles fondés sur le flux de chaleur à l'intérieur des planètes géantes[62]. À titre de comparaison, cette intensité est de 4,3 G pour Jupiter et de 0,5 G pour la Terre.

Notes et références

Robert Halleux, « Les noms latins de la pierre d’aimant et les premières mentions de la boussole en Occident », Comptes rendus des séances de l'Académie des Inscriptions et Belles-Lettres, vol. 156, n^o 3,‎ 2012, p. 1263–1270 (DOI 10.3406/crai.2012.93693, lire en ligne, consulté le 21 juillet 2021)
« Teaching about the Earth's Magnetism in Earth Sciences--Part 2 », sur pwg.gsfc.nasa.gov (consulté le 21 juillet 2021)
(en-GB) « William Gilbert - MagLab », sur nationalmaglab.org (consulté le 31 mai 2021)
(en) David J. Stevenson, « Planetary magnetic fields », Earth and Planetary Science Letters, vol. 208, n^os 1-2,‎ mars 2003, p. 1–11 (DOI 10.1016/S0012-821X(02)01126-3, lire en ligne, consulté le 6 juin 2021)
(en) Ulrich Christensen, « Planetary magnetic fields »
Pierre AUGIER, Dynamo Bullard-Von Kármán gallium, Lyon (lire en ligne)
(en) Peter Olson et Ulrich R. Christensen, « Dipole moment scaling for convection-driven planetary dynamos », Earth and Planetary Science Letters, vol. 250, n^os 3-4,‎ octobre 2006, p. 561–571 (DOI 10.1016/j.epsl.2006.08.008, lire en ligne, consulté le 1^er août 2021).
« Savoirs ENS », sur savoirs.ens.fr (consulté le 31 juillet 2021)
« Magnetic Reversals », sur www.geomag.bgs.ac.uk (consulté le 31 juillet 2021)
(en) C. Gissinger, « A new deterministic model for chaotic reversals », The European Physical Journal B, vol. 85, n^o 4,‎ avril 2012, p. 137 (ISSN 1434-6028 et 1434-6036, DOI 10.1140/epjb/e2012-20799-5, lire en ligne, consulté le 31 juillet 2021)
(en) H. K. Moffatt, « A self-consistent treatment of simple dynamo systems », Geophysical & Astrophysical Fluid Dynamics, vol. 14, n^o 1,‎ janvier 1979, p. 147–166 (ISSN 0309-1929 et 1029-0419, DOI 10.1080/03091927908244536, lire en ligne, consulté le 2 août 2021)
(en) C. Laroche, R. Labbé, F. Pétrélis et S. Fauve, « Chaotic motors », American Journal of Physics, vol. 80, n^o 2,‎ février 2012, p. 113–121 (ISSN 0002-9505 et 1943-2909, DOI 10.1119/1.3664605, lire en ligne, consulté le 2 août 2021)
Ahmad Harb et Nabil Ayoub, « On Slide Mode Control of Chaotic Rikitake Two-Disk Dynamo—Chaotic Simulations of the Reversals of the Earth’s Magnetic Field », International Journal of Modern Nonlinear Theory and Application, vol. 03, n^o 03,‎ 2014, p. 136–143 (ISSN 2167-9479 et 2167-9487, DOI 10.4236/ijmnta.2014.33015, lire en ligne, consulté le 5 août 2021)
(en) D. Volobuev, « “TOY” Dynamo to Describe the Long-Term Solar Activity Cycles », Solar Physics, vol. 238, n^o 2,‎ novembre 2006, p. 421–430 (ISSN 0038-0938 et 1573-093X, DOI 10.1007/s11207-006-0154-x, lire en ligne, consulté le 26 août 2021)
(en) P. Mininni, P. Dmitruk, P. Odier et J.-F. Pinton, « Long-term memory in experiments and numerical simulations of hydrodynamic and magnetohydrodynamic turbulence », Physical Review E, vol. 89, n^o 5,‎ 8 mai 2014, p. 053005 (ISSN 1539-3755 et 1550-2376, DOI 10.1103/PhysRevE.89.053005, lire en ligne, consulté le 8 août 2021)
« VKS - von Karman Sodium - Collaboration WebPage », sur perso.ens-lyon.fr (consulté le 26 août 2021)
(en) Zahra Koochak et Antony C. Fraser‐Smith, « An Update on the Centered and Eccentric Geomagnetic Dipoles and Their Poles for the Years 1980–2015 », Earth and Space Science, vol. 4, n^o 10,‎ octobre 2017, p. 626–636 (ISSN 2333-5084 et 2333-5084, DOI 10.1002/2017EA000280, lire en ligne, consulté le 1^er juillet 2021)
(en) J. E. P. Connerney, Mario H. Acuña et Norman F. Ness, « The magnetic field of Neptune », Journal of Geophysical Research, vol. 96, n^o S01,‎ 1991, p. 19023 (ISSN 0148-0227, DOI 10.1029/91JA01165, lire en ligne, consulté le 1^er juillet 2021)
(en) N. F. Ness, K. W. Behannon, R. P. Lepping et Y. C. Whang, « The magnetic field of Mercury, 1 », Journal of Geophysical Research, vol. 80, n^o 19,‎ 1^er juillet 1975, p. 2708–2716 (DOI 10.1029/JA080i019p02708, lire en ligne, consulté le 11 juillet 2021)
(en-GB) « Molten core solves mystery of Mercury's magnetic field », sur Physics World, 4 mai 2007 (consulté le 11 juillet 2021)
(en) Francis Nimmo, « Why does Venus lack a magnetic field? », Geology, vol. 30, n^o 11,‎ 1^er novembre 2002, p. 987–990 (ISSN 0091-7613, DOI 10.1130/0091-7613(2002)0302.0.CO;2, lire en ligne, consulté le 31 mai 2021)
(en) D. L. Mitchell, J. S. Halekas, R. P. Lin et S. Frey, « Global mapping of lunar crustal magnetic fields by Lunar Prospector », Icarus, vol. 194,‎ 1^er avril 2008, p. 401-409 (DOI 10.1016/j.icarus.2007.10.027, lire en ligne, consulté le 4 décembre 2020).
(en) S. Mighani, H. Wang, D.L. Shuster et C.S. Borlina, « The end of the lunar dynamo », Science Advances, vol. 6, n^o 1,‎ 2020, eaax0883 (PMID 31911941, PMCID 6938704, DOI 10.1126/sciadv.aax0883, Bibcode 2020SciA....6..883M).
Matthieu Laneuville, « La Lune, une histoire pleine de surprises », sur www.pourlascience.fr, 27 juillet 2016 (consulté le 5 décembre 2020).
(en) B. E. Strauss, S. M. Tikoo, J. Gross, J. B. Setera et B. Turrin, « Constraining the Decline of the Lunar Dynamo Field at ≈3.1 Ga Through Paleomagnetic Analyses of Apollo 12 Mare Basalts », JG-Planets, vol. 126, n^o 3,‎ mars 2021, article n^o e2020JE006715 (DOI 10.1029/2020JE006715).
(en) B. E. Strauss, S. M. Tikoo, J. Gross, J. B. Setera et B. Turrin, « Constraining the Decline of the Lunar Dynamo Field at ≈3.1 Ga Through Paleomagnetic Analyses of Apollo 12 Mare Basalts », JGR Planets, vol. 126, n^o 3,‎ mars 2021, article n^o e2020JE006715 (DOI 10.1029/2020JE006715).
(en) Catherine L. Johnson, Anna Mittelholz, Benoit Langlais et Christopher T. Russell, « Crustal and time-varying magnetic fields at the InSight landing site on Mars », Nature Geoscience, vol. 13, n^o 3,‎ mars 2020, p. 199–204 (ISSN 1752-0894 et 1752-0908, DOI 10.1038/s41561-020-0537-x, lire en ligne, consulté le 31 mai 2021).
(en) Constantin Sandu et Walter S. Kiefer, « Degassing history of Mars and the lifespan of its magnetic dynamo: MARS MAGNETIC FIELD AND DEGASSING », Geophysical Research Letters, vol. 39, n^o 3,‎ février 2012, n/a–n/a (DOI 10.1029/2011GL050225, lire en ligne, consulté le 31 juillet 2021)
(en) C. T. Russell et M. K. Dougherty, « Magnetic Fields of the Outer Planets », Space Science Reviews, vol. 152, n^os 1-4,‎ mai 2010, p. 251–269 (ISSN 0038-6308 et 1572-9672, DOI 10.1007/s11214-009-9621-7, lire en ligne, consulté le 31 mai 2021)
(en) James W. Warwick, « Radio Emission from Jupiter », Annual Review of Astronomy and Astrophysics, vol. 2, n^o 1,‎ septembre 1964, p. 1–22 (ISSN 0066-4146 et 1545-4282, DOI 10.1146/annurev.aa.02.090164.000245, lire en ligne, consulté le 3 juillet 2021).
George B. Field, « A Model for the Decimeter Radiation by Jupiter. », The Astronomical Journal, vol. 65,‎ 1960, p. 344 (ISSN 0004-6256, DOI 10.1086/108073, lire en ligne, consulté le 11 juillet 2021).
(en) J. E. P. Connerney, M. Benn, J. B. Bjarno et T. Denver, « The Juno Magnetic Field Investigation », Space Science Reviews, vol. 213, n^os 1-4,‎ novembre 2017, p. 39–138 (ISSN 0038-6308 et 1572-9672, DOI 10.1007/s11214-017-0334-z, lire en ligne, consulté le 13 juillet 2021)
(en) M.G. Kivelson, K.K. Khurana et M. Volwerk, « The Permanent and Inductive Magnetic Moments of Ganymede », Icarus, vol. 157, n^o 2,‎ juin 2002, p. 507–522 (DOI 10.1006/icar.2002.6834, lire en ligne, consulté le 2 juillet 2021)
(en) David J. Stevenson, « Planetary Magnetic Fields: Achievements and Prospects », Space Science Reviews, vol. 152, n^os 1-4,‎ mai 2010, p. 651–664 (ISSN 0038-6308 et 1572-9672, DOI 10.1007/s11214-009-9572-z, lire en ligne, consulté le 22 juillet 2021)
(en) Tina Rückriemen, Doris Breuer et Tilman Spohn, « Top-down freezing in a Fe–FeS core and Ganymede’s present-day magnetic field », Icarus, vol. 307,‎ juin 2018, p. 172–196 (DOI 10.1016/j.icarus.2018.02.021, lire en ligne, consulté le 10 juillet 2021)
(en) M. K. Dougherty, H. Cao, K. K. Khurana et G. J. Hunt, « Saturn's Magnetic Field from the Cassini Grand Finale orbits », AGU Fall Meeting Abstracts, vol. 22,‎ 1^er décembre 2017 (lire en ligne, consulté le 11 juillet 2021).
(en) B. R. Sandel et A. L. Broadfoot, « Morphology of Saturn's aurora », Nature, vol. 292, n^o 5825,‎ août 1981, p. 679–682 (ISSN 0028-0836 et 1476-4687, DOI 10.1038/292679a0, lire en ligne, consulté le 11 juillet 2021).
(en) Fritz M. Neubauer, « Possible strengths of dynamo magnetic fields of the Galilean satellites and of Titan », Geophysical Research Letters, vol. 5, n^o 11,‎ novembre 1978, p. 905–908 (DOI 10.1029/GL005i011p00905, lire en ligne, consulté le 14 juillet 2021).
(en) C.A. Nixon, R.D. Lorenz, R.K. Achterberg et A. Buch, « Titan's cold case files - Outstanding questions after Cassini-Huygens », Planetary and Space Science, vol. 155,‎ juin 2018, p. 50–72 (DOI 10.1016/j.pss.2018.02.009, lire en ligne, consulté le 14 juillet 2021).
(en) Richard S. Selesnick, « Magnetospheric convection in the nondipolar magnetic field of Uranus », Journal of Geophysical Research, vol. 93, n^o A9,‎ 1988, p. 9607 (ISSN 0148-0227, DOI 10.1029/JA093iA09p09607, lire en ligne, consulté le 1^er juillet 2021)
(en) Norman F. Ness, « Space Exploration of Planetary Magnetism », Space Science Reviews, vol. 152, n^os 1-4,‎ mai 2010, p. 5–22 (ISSN 0038-6308 et 1572-9672, DOI 10.1007/s11214-009-9567-9, lire en ligne, consulté le 1^er juillet 2021)
(en) S Stanley et J Bloxham, « Numerical dynamo models of Uranus' and Neptune's magnetic fields », Icarus, vol. 184, n^o 2,‎ octobre 2006, p. 556–572 (DOI 10.1016/j.icarus.2006.05.005, lire en ligne, consulté le 3 juillet 2021)
(en) James F.J. Bryson, Jerome A. Neufeld et Francis Nimmo, « Constraints on asteroid magnetic field evolution and the radii of meteorite parent bodies from thermal modelling », Earth and Planetary Science Letters, vol. 521,‎ septembre 2019, p. 68–78 (DOI 10.1016/j.epsl.2019.05.046, lire en ligne, consulté le 1^er août 2021).
(en) J. M. Herndon et M. W. Rowe, « Magnetism in meteorites », Meteoritics, vol. 9,‎ 31 décembre 1974, p. 289-305 (DOI 10.1111/j.1945-5100.1974.tb01197.x, présentation en ligne, lire en ligne [PDF], consulté le 23 août 2019).
(en) James F. J. Bryson, Francis Nimmo et Richard J. Harrison, « Magnetic meteorites and the early solar system », Astronomy & Geophysics (en), vol. 56, n^o 4,‎ août 2015, p. 36-42 (lire en ligne [PDF], consulté le 29 août 2019).
(en) F. J. Bryson, Julia Herrero-Albillos, Florian Kronast, Massimo Ghidini et Simon A. T. Redfern, « Nanopaleomagnetism of meteoritic Fe–Ni studied using X-ray photoemission electron microscopy », Earth and Planetary Science Letters, vol. 396,‎ 15 juin 2014, p. 125-133 (DOI 10.1016/j.epsl.2014.04.016, lire en ligne [PDF], consulté le 30 août 2019).
(en) John A. Tarduno, Rory D. Cottrell, Francis Nimmo, Julianna Hopkins, Julia Voronov et al., « Evidence for a Dynamo in the Main Group Pallasite Parent Body », Science, vol. 338, n^o 6109,‎ 16 novembre 2012, p. 939-942 (DOI 10.1126/science.1223932).
(en) Emily Poore, « The Long-Lived Magnetic Fields of Meteorites », sur Sky & Telescope, 29 janvier 2015 (consulté le 27 août 2019).
(en) James F. J. Bryson, Claire I. O. Nichols, Julia Herrero-Albillos, Florian Kronast, Takeshi Kasama et al., « Long-lived magnetism from solidification-driven convection on the pallasite parent body », Nature, vol. 517,‎ 21 janvier 2015, p. 472-475 (DOI 10.1038/nature14114).
(en) Roger R. Fu, Benjamin P. Weiss, David L. Shuster, Jérôme Gattacceca, Timothy L. Grove et al., « An Ancient Core Dynamo in Asteroid Vesta », Science, vol. 338, n^o 6104,‎ 12 octobre 2012, p. 238-241 (DOI 10.1126/science.1225648).
(en) B. P. Weiss, E. A. Lima et M. E. Zucolotto, « Magnetism on the Angrite Parent Body », 39(th) Lunar and Planetary Science Conference,‎ mars 2008 (lire en ligne [PDF], consulté le 23 juillet 2019).
(en) Benjamin P. Weiss, James S. Berdahl, Linda Elkins-Tanton, Sabine Stanley, Eduardo A. Lima et Laurent Carporzen, « Magnetism on the Angrite Parent Body and the Early Differentiation of Planetesimals », Science, vol. 322, n^o 5902,‎ 31 octobre 2008, p. 713-716 (DOI 10.1126/science.1162459).
(en) G. Kletetschka, T. Kohout et P. J. Wasilewski, « Magnetic remanence in the Murchison meteorite », Meteoritics & Planetary Science, vol. 38, n^o 3,‎ 2003, p. 399-405 (lire en ligne, consulté le 24 juillet 2019).
(en) R. R. Fu, E. A. Lima et B. P. Weiss, « No nebular magnetization in the Allende CV carbonaceous chondrite », Earth and Planetary Science Letters, vol. 404,‎ 15 octobre 2014, p. 54-66 (DOI 10.1016/j.epsl.2014.07.014).
(en) « Vigarano Mainarda », sur Mindat.org (consulté le 24 juillet 2019).
(en) Jay Shah, Helena C. Bates, Adrian R. Muxworthy, Dominik C. Hezel, Sara S. Russell et Matthew J. Genge, « Long-lived magnetism on chondrite parent bodies », Earth and Planetary Science Letters, vol. 475,‎ 1^er octobre 2017, p. 106-118 (DOI 10.1016/j.epsl.2017.07.035).
(en) « Farmington meteorite », sur Mindat.org (consulté le 23 juillet 2019).
(en) M. W. Rowe, « Constraints on magnetic field which magnetized the Farmington meteorite parent body », Meteoritics & Planetary Science, vol. 10, n^o 1,‎ avril 1975, p. 23-30 (DOI 10.1111/j.1945-5100.1975.tb00004.x, lire en ligne [PDF], consulté le 23 juillet 2019).
(en) « Bjurböle meteorite », sur Mindat.org (consulté le 24 juillet 2019).
(en) J. F. J. Bryson, B. P. Weiss, B. Getzin, J. N. H. Abrahams, F. Nimmo et al., « Paleomagnetic Evidence for a Partially Differentiated Ordinary Chondrite Parent Asteroid », JGR Planets, vol. 124, n^o 7,‎ juillet 2019, p. 1880-1898 (DOI 10.1029/2019JE005951).
(en) Hector Javier Durand-Manterola, « Dipolar Magnetic Moment of the Bodies of the Solar System and the Hot Jupiters », Published in Planetary and Space Science,‎ 2009
(en) P. Wilson Cauley, Evgenya L. Shkolnik, Joe Llama et Antonino F. Lanza, « Magnetic field strengths of hot Jupiters from signals of star–planet interactions », Nature Astronomy, vol. 3,‎ 22 juillet 2019, p. 1128-1134 (DOI 10.1038/s41550-019-0840-x).

Voir aussi

Portail de la physique
Portail de l’astronomie
Portail des planètes mineures et comètes
Portail des exoplanètes

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Robert Halleux, « Les noms latins de la pierre d’aimant et les premières mentions de la boussole en Occident », Comptes rendus des séances de l'Académie des Inscriptions et Belles-Lettres, vol. 156, n^o 3,‎ 2012, p. 1263–1270 (DOI 10.3406/crai.2012.93693, lire en ligne, consulté le 21 juillet 2021)

[2] « Teaching about the Earth's Magnetism in Earth Sciences--Part 2 », sur pwg.gsfc.nasa.gov (consulté le 21 juillet 2021)

[3] (en-GB) « William Gilbert - MagLab », sur nationalmaglab.org (consulté le 31 mai 2021)

[stevenson-4] (en) David J. Stevenson, « Planetary magnetic fields », Earth and Planetary Science Letters, vol. 208, n^os 1-2,‎ mars 2003, p. 1–11 (DOI 10.1016/S0012-821X(02)01126-3, lire en ligne, consulté le 6 juin 2021)

[5] (en) Ulrich Christensen, « Planetary magnetic fields »

[6] Pierre AUGIER, Dynamo Bullard-Von Kármán gallium, Lyon (lire en ligne)

[olson-7] (en) Peter Olson et Ulrich R. Christensen, « Dipole moment scaling for convection-driven planetary dynamos », Earth and Planetary Science Letters, vol. 250, n^os 3-4,‎ octobre 2006, p. 561–571 (DOI 10.1016/j.epsl.2006.08.008, lire en ligne, consulté le 1^er août 2021).

[8] « Savoirs ENS », sur savoirs.ens.fr (consulté le 31 juillet 2021)

[9] « Magnetic Reversals », sur www.geomag.bgs.ac.uk (consulté le 31 juillet 2021)

[10] (en) C. Gissinger, « A new deterministic model for chaotic reversals », The European Physical Journal B, vol. 85, n^o 4,‎ avril 2012, p. 137 (ISSN 1434-6028 et 1434-6036, DOI 10.1140/epjb/e2012-20799-5, lire en ligne, consulté le 31 juillet 2021)

[Moffatt-11] (en) H. K. Moffatt, « A self-consistent treatment of simple dynamo systems », Geophysical & Astrophysical Fluid Dynamics, vol. 14, n^o 1,‎ janvier 1979, p. 147–166 (ISSN 0309-1929 et 1029-0419, DOI 10.1080/03091927908244536, lire en ligne, consulté le 2 août 2021)

[chaotic-12] (en) C. Laroche, R. Labbé, F. Pétrélis et S. Fauve, « Chaotic motors », American Journal of Physics, vol. 80, n^o 2,‎ février 2012, p. 113–121 (ISSN 0002-9505 et 1943-2909, DOI 10.1119/1.3664605, lire en ligne, consulté le 2 août 2021)

[13] Ahmad Harb et Nabil Ayoub, « On Slide Mode Control of Chaotic Rikitake Two-Disk Dynamo—Chaotic Simulations of the Reversals of the Earth’s Magnetic Field », International Journal of Modern Nonlinear Theory and Application, vol. 03, n^o 03,‎ 2014, p. 136–143 (ISSN 2167-9479 et 2167-9487, DOI 10.4236/ijmnta.2014.33015, lire en ligne, consulté le 5 août 2021)

[14] (en) D. Volobuev, « “TOY” Dynamo to Describe the Long-Term Solar Activity Cycles », Solar Physics, vol. 238, n^o 2,‎ novembre 2006, p. 421–430 (ISSN 0038-0938 et 1573-093X, DOI 10.1007/s11207-006-0154-x, lire en ligne, consulté le 26 août 2021)

[15] (en) P. Mininni, P. Dmitruk, P. Odier et J.-F. Pinton, « Long-term memory in experiments and numerical simulations of hydrodynamic and magnetohydrodynamic turbulence », Physical Review E, vol. 89, n^o 5,‎ 8 mai 2014, p. 053005 (ISSN 1539-3755 et 1550-2376, DOI 10.1103/PhysRevE.89.053005, lire en ligne, consulté le 8 août 2021)

[16] « VKS - von Karman Sodium - Collaboration WebPage », sur perso.ens-lyon.fr (consulté le 26 août 2021)

[17] (en) Zahra Koochak et Antony C. Fraser‐Smith, « An Update on the Centered and Eccentric Geomagnetic Dipoles and Their Poles for the Years 1980–2015 », Earth and Space Science, vol. 4, n^o 10,‎ octobre 2017, p. 626–636 (ISSN 2333-5084 et 2333-5084, DOI 10.1002/2017EA000280, lire en ligne, consulté le 1^er juillet 2021)

[Connerney-18] (en) J. E. P. Connerney, Mario H. Acuña et Norman F. Ness, « The magnetic field of Neptune », Journal of Geophysical Research, vol. 96, n^o S01,‎ 1991, p. 19023 (ISSN 0148-0227, DOI 10.1029/91JA01165, lire en ligne, consulté le 1^er juillet 2021)

[19] (en) N. F. Ness, K. W. Behannon, R. P. Lepping et Y. C. Whang, « The magnetic field of Mercury, 1 », Journal of Geophysical Research, vol. 80, n^o 19,‎ 1^er juillet 1975, p. 2708–2716 (DOI 10.1029/JA080i019p02708, lire en ligne, consulté le 11 juillet 2021)

[20] (en-GB) « Molten core solves mystery of Mercury's magnetic field », sur Physics World, 4 mai 2007 (consulté le 11 juillet 2021)

[pubs.geoscienceworld.org-21] (en) Francis Nimmo, « Why does Venus lack a magnetic field? », Geology, vol. 30, n^o 11,‎ 1^er novembre 2002, p. 987–990 (ISSN 0091-7613, DOI 10.1130/0091-7613(2002)0302.0.CO;2, lire en ligne, consulté le 31 mai 2021)

[22] (en) D. L. Mitchell, J. S. Halekas, R. P. Lin et S. Frey, « Global mapping of lunar crustal magnetic fields by Lunar Prospector », Icarus, vol. 194,‎ 1^er avril 2008, p. 401-409 (DOI 10.1016/j.icarus.2007.10.027, lire en ligne, consulté le 4 décembre 2020).

[Mighani2020-23] (en) S. Mighani, H. Wang, D.L. Shuster et C.S. Borlina, « The end of the lunar dynamo », Science Advances, vol. 6, n^o 1,‎ 2020, eaax0883 (PMID 31911941, PMCID 6938704, DOI 10.1126/sciadv.aax0883, Bibcode 2020SciA....6..883M).

[pourlascience-24] Matthieu Laneuville, « La Lune, une histoire pleine de surprises », sur www.pourlascience.fr, 27 juillet 2016 (consulté le 5 décembre 2020).

[25] (en) B. E. Strauss, S. M. Tikoo, J. Gross, J. B. Setera et B. Turrin, « Constraining the Decline of the Lunar Dynamo Field at ≈3.1 Ga Through Paleomagnetic Analyses of Apollo 12 Mare Basalts », JG-Planets, vol. 126, n^o 3,‎ mars 2021, article n^o e2020JE006715 (DOI 10.1029/2020JE006715).

[26] (en) B. E. Strauss, S. M. Tikoo, J. Gross, J. B. Setera et B. Turrin, « Constraining the Decline of the Lunar Dynamo Field at ≈3.1 Ga Through Paleomagnetic Analyses of Apollo 12 Mare Basalts », JGR Planets, vol. 126, n^o 3,‎ mars 2021, article n^o e2020JE006715 (DOI 10.1029/2020JE006715).

[:0-27] (en) Catherine L. Johnson, Anna Mittelholz, Benoit Langlais et Christopher T. Russell, « Crustal and time-varying magnetic fields at the InSight landing site on Mars », Nature Geoscience, vol. 13, n^o 3,‎ mars 2020, p. 199–204 (ISSN 1752-0894 et 1752-0908, DOI 10.1038/s41561-020-0537-x, lire en ligne, consulté le 31 mai 2021).

[28] (en) Constantin Sandu et Walter S. Kiefer, « Degassing history of Mars and the lifespan of its magnetic dynamo: MARS MAGNETIC FIELD AND DEGASSING », Geophysical Research Letters, vol. 39, n^o 3,‎ février 2012, n/a–n/a (DOI 10.1029/2011GL050225, lire en ligne, consulté le 31 juillet 2021)

[29] (en) C. T. Russell et M. K. Dougherty, « Magnetic Fields of the Outer Planets », Space Science Reviews, vol. 152, n^os 1-4,‎ mai 2010, p. 251–269 (ISSN 0038-6308 et 1572-9672, DOI 10.1007/s11214-009-9621-7, lire en ligne, consulté le 31 mai 2021)

[30] (en) James W. Warwick, « Radio Emission from Jupiter », Annual Review of Astronomy and Astrophysics, vol. 2, n^o 1,‎ septembre 1964, p. 1–22 (ISSN 0066-4146 et 1545-4282, DOI 10.1146/annurev.aa.02.090164.000245, lire en ligne, consulté le 3 juillet 2021).

[31] George B. Field, « A Model for the Decimeter Radiation by Jupiter. », The Astronomical Journal, vol. 65,‎ 1960, p. 344 (ISSN 0004-6256, DOI 10.1086/108073, lire en ligne, consulté le 11 juillet 2021).

[32] (en) J. E. P. Connerney, M. Benn, J. B. Bjarno et T. Denver, « The Juno Magnetic Field Investigation », Space Science Reviews, vol. 213, n^os 1-4,‎ novembre 2017, p. 39–138 (ISSN 0038-6308 et 1572-9672, DOI 10.1007/s11214-017-0334-z, lire en ligne, consulté le 13 juillet 2021)

[kivel-33] (en) M.G. Kivelson, K.K. Khurana et M. Volwerk, « The Permanent and Inductive Magnetic Moments of Ganymede », Icarus, vol. 157, n^o 2,‎ juin 2002, p. 507–522 (DOI 10.1006/icar.2002.6834, lire en ligne, consulté le 2 juillet 2021)

[achpro-34] (en) David J. Stevenson, « Planetary Magnetic Fields: Achievements and Prospects », Space Science Reviews, vol. 152, n^os 1-4,‎ mai 2010, p. 651–664 (ISSN 0038-6308 et 1572-9672, DOI 10.1007/s11214-009-9572-z, lire en ligne, consulté le 22 juillet 2021)

[Juno-35] (en) Tina Rückriemen, Doris Breuer et Tilman Spohn, « Top-down freezing in a Fe–FeS core and Ganymede’s present-day magnetic field », Icarus, vol. 307,‎ juin 2018, p. 172–196 (DOI 10.1016/j.icarus.2018.02.021, lire en ligne, consulté le 10 juillet 2021)

[36] (en) M. K. Dougherty, H. Cao, K. K. Khurana et G. J. Hunt, « Saturn's Magnetic Field from the Cassini Grand Finale orbits », AGU Fall Meeting Abstracts, vol. 22,‎ 1^er décembre 2017 (lire en ligne, consulté le 11 juillet 2021).

[37] (en) B. R. Sandel et A. L. Broadfoot, « Morphology of Saturn's aurora », Nature, vol. 292, n^o 5825,‎ août 1981, p. 679–682 (ISSN 0028-0836 et 1476-4687, DOI 10.1038/292679a0, lire en ligne, consulté le 11 juillet 2021).

[38] (en) Fritz M. Neubauer, « Possible strengths of dynamo magnetic fields of the Galilean satellites and of Titan », Geophysical Research Letters, vol. 5, n^o 11,‎ novembre 1978, p. 905–908 (DOI 10.1029/GL005i011p00905, lire en ligne, consulté le 14 juillet 2021).

[39] (en) C.A. Nixon, R.D. Lorenz, R.K. Achterberg et A. Buch, « Titan's cold case files - Outstanding questions after Cassini-Huygens », Planetary and Space Science, vol. 155,‎ juin 2018, p. 50–72 (DOI 10.1016/j.pss.2018.02.009, lire en ligne, consulté le 14 juillet 2021).

[40] (en) Richard S. Selesnick, « Magnetospheric convection in the nondipolar magnetic field of Uranus », Journal of Geophysical Research, vol. 93, n^o A9,‎ 1988, p. 9607 (ISSN 0148-0227, DOI 10.1029/JA093iA09p09607, lire en ligne, consulté le 1^er juillet 2021)

[ness-41] (en) Norman F. Ness, « Space Exploration of Planetary Magnetism », Space Science Reviews, vol. 152, n^os 1-4,‎ mai 2010, p. 5–22 (ISSN 0038-6308 et 1572-9672, DOI 10.1007/s11214-009-9567-9, lire en ligne, consulté le 1^er juillet 2021)

[42] (en) S Stanley et J Bloxham, « Numerical dynamo models of Uranus' and Neptune's magnetic fields », Icarus, vol. 184, n^o 2,‎ octobre 2006, p. 556–572 (DOI 10.1016/j.icarus.2006.05.005, lire en ligne, consulté le 3 juillet 2021)

[43] (en) James F.J. Bryson, Jerome A. Neufeld et Francis Nimmo, « Constraints on asteroid magnetic field evolution and the radii of meteorite parent bodies from thermal modelling », Earth and Planetary Science Letters, vol. 521,‎ septembre 2019, p. 68–78 (DOI 10.1016/j.epsl.2019.05.046, lire en ligne, consulté le 1^er août 2021).

[44] (en) J. M. Herndon et M. W. Rowe, « Magnetism in meteorites », Meteoritics, vol. 9,‎ 31 décembre 1974, p. 289-305 (DOI 10.1111/j.1945-5100.1974.tb01197.x, présentation en ligne, lire en ligne [PDF], consulté le 23 août 2019).

[BrysonNimmo2015-45] (en) James F. J. Bryson, Francis Nimmo et Richard J. Harrison, « Magnetic meteorites and the early solar system », Astronomy & Geophysics (en), vol. 56, n^o 4,‎ août 2015, p. 36-42 (lire en ligne [PDF], consulté le 29 août 2019).

[46] (en) F. J. Bryson, Julia Herrero-Albillos, Florian Kronast, Massimo Ghidini et Simon A. T. Redfern, « Nanopaleomagnetism of meteoritic Fe–Ni studied using X-ray photoemission electron microscopy », Earth and Planetary Science Letters, vol. 396,‎ 15 juin 2014, p. 125-133 (DOI 10.1016/j.epsl.2014.04.016, lire en ligne [PDF], consulté le 30 août 2019).

[47] (en) John A. Tarduno, Rory D. Cottrell, Francis Nimmo, Julianna Hopkins, Julia Voronov et al., « Evidence for a Dynamo in the Main Group Pallasite Parent Body », Science, vol. 338, n^o 6109,‎ 16 novembre 2012, p. 939-942 (DOI 10.1126/science.1223932).

[Poore2015-48] (en) Emily Poore, « The Long-Lived Magnetic Fields of Meteorites », sur Sky & Telescope, 29 janvier 2015 (consulté le 27 août 2019).

[BrysonNichols2015-49] (en) James F. J. Bryson, Claire I. O. Nichols, Julia Herrero-Albillos, Florian Kronast, Takeshi Kasama et al., « Long-lived magnetism from solidification-driven convection on the pallasite parent body », Nature, vol. 517,‎ 21 janvier 2015, p. 472-475 (DOI 10.1038/nature14114).

[50] (en) Roger R. Fu, Benjamin P. Weiss, David L. Shuster, Jérôme Gattacceca, Timothy L. Grove et al., « An Ancient Core Dynamo in Asteroid Vesta », Science, vol. 338, n^o 6104,‎ 12 octobre 2012, p. 238-241 (DOI 10.1126/science.1225648).

[51] (en) B. P. Weiss, E. A. Lima et M. E. Zucolotto, « Magnetism on the Angrite Parent Body », 39(th) Lunar and Planetary Science Conference,‎ mars 2008 (lire en ligne [PDF], consulté le 23 juillet 2019).

[52] (en) Benjamin P. Weiss, James S. Berdahl, Linda Elkins-Tanton, Sabine Stanley, Eduardo A. Lima et Laurent Carporzen, « Magnetism on the Angrite Parent Body and the Early Differentiation of Planetesimals », Science, vol. 322, n^o 5902,‎ 31 octobre 2008, p. 713-716 (DOI 10.1126/science.1162459).

[53] (en) G. Kletetschka, T. Kohout et P. J. Wasilewski, « Magnetic remanence in the Murchison meteorite », Meteoritics & Planetary Science, vol. 38, n^o 3,‎ 2003, p. 399-405 (lire en ligne, consulté le 24 juillet 2019).

[54] (en) R. R. Fu, E. A. Lima et B. P. Weiss, « No nebular magnetization in the Allende CV carbonaceous chondrite », Earth and Planetary Science Letters, vol. 404,‎ 15 octobre 2014, p. 54-66 (DOI 10.1016/j.epsl.2014.07.014).

[55] (en) « Vigarano Mainarda », sur Mindat.org (consulté le 24 juillet 2019).

[Shah2017-56] (en) Jay Shah, Helena C. Bates, Adrian R. Muxworthy, Dominik C. Hezel, Sara S. Russell et Matthew J. Genge, « Long-lived magnetism on chondrite parent bodies », Earth and Planetary Science Letters, vol. 475,‎ 1^er octobre 2017, p. 106-118 (DOI 10.1016/j.epsl.2017.07.035).

[57] (en) « Farmington meteorite », sur Mindat.org (consulté le 23 juillet 2019).

[58] (en) M. W. Rowe, « Constraints on magnetic field which magnetized the Farmington meteorite parent body », Meteoritics & Planetary Science, vol. 10, n^o 1,‎ avril 1975, p. 23-30 (DOI 10.1111/j.1945-5100.1975.tb00004.x, lire en ligne [PDF], consulté le 23 juillet 2019).

[59] (en) « Bjurböle meteorite », sur Mindat.org (consulté le 24 juillet 2019).

[60] (en) J. F. J. Bryson, B. P. Weiss, B. Getzin, J. N. H. Abrahams, F. Nimmo et al., « Paleomagnetic Evidence for a Partially Differentiated Ordinary Chondrite Parent Asteroid », JGR Planets, vol. 124, n^o 7,‎ juillet 2019, p. 1880-1898 (DOI 10.1029/2019JE005951).

[:1-61] (en) Hector Javier Durand-Manterola, « Dipolar Magnetic Moment of the Bodies of the Solar System and the Hot Jupiters », Published in Planetary and Space Science,‎ 2009

[62] (en) P. Wilson Cauley, Evgenya L. Shkolnik, Joe Llama et Antonino F. Lanza, « Magnetic field strengths of hot Jupiters from signals of star–planet interactions », Nature Astronomy, vol. 3,‎ 22 juillet 2019, p. 1128-1134 (DOI 10.1038/s41550-019-0840-x).