Conjecture de Keller

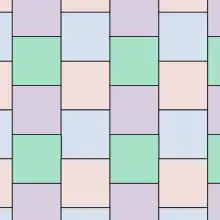
En géométrie, la conjecture de Keller est la conjecture introduite par Ott-Heinrich Keller (de) en 1930 que dans tout pavage de l'espace euclidien par des hypercubes identiques, on trouve deux hypercubes qui ont une face entière en commun. Par exemple, comme illustré ci-contre, dans tout pavage du plan par des carrés identiques, il y a une paire de carrés qui ont un côté entier en commun.

Pour la conjecture de Keller sur les fonctions polynomiales voir la conjecture jacobienne.

Dans ce pavage du plan par des carrés congruents, les carrés verts et violets ont un côté entier en commun ainsi que les carrés bleus et orange.

Cette conjecture de Keller a été montrée dans les dimensions inférieures ou égales à 6 par Oskar Perron en 1940. Mais pour des dimensions supérieures cette conjecture est fausse, comme montré en dimension 10 et plus par Jeffrey Lagarias et Peter Shor en 1992, puis à partir de la dimension 8 par John Mackey en 2002, via une reformulation du problème en termes de cliques de certains graphes, aujourd'hui appelés graphes de Keller. Enfin, en 2019, une preuve assistée par ordinateur d'environ 200 Go utilisant ces graphes a permis d'établir que la conjecture est vraie en dimension 7[1]^,[2]^,[3]^,[4]^,[5]. Par conséquent, cela résout la question posée par Keller : la conjecture est vraie jusqu'en dimension 7, et fausse dans les dimensions supérieures à 7.