Conjecture de Kelvin

La conjecture de Kelvin, énoncée pour la première fois par le physicien et mathématicien Lord Kelvin, présente la question de la recherche d'un nid d'abeille (c'est-à-dire un pavage de l'espace R³) par des cellules de volumes identiques et de surface minimale.

Pavage que Kelvin présumait optimal

Contre-exemple de Weaire–Phelan

Le savant énonça en 1887 qu'un pavage par l'octaèdre tronqué à 14 faces (8 hexagones, légèrement incurvés pour satisfaire aux conditions de Plateau, et 6 carrés) était la solution optimale du problème. Durant un siècle, les chercheurs ont essayé de démontrer ou d'infirmer ce résultat. La majorité des spécialistes (y compris Hermann Weyl en 1952) pensait qu'il était vrai.

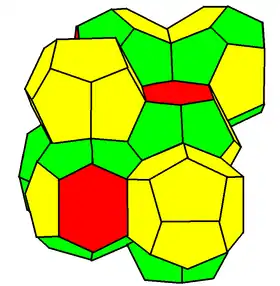
Mais en 1994, Denis Weaire (en) et son étudiant Robert Phelan ont trouvé un contre-exemple, la structure de Weaire-Phelan. On peut paver l'espace par répétitions de cette cellule, composée de huit polyèdres à faces irrégulières : six tétradécaèdres (à 2 faces hexagonales et 12 pentagonales) et deux pyritoèdres (dodécaèdres à faces pentagonales ; cette fois, ce sont les pentagones qui sont incurvés).

On pensait que cette structure, meilleure que celle de Kelvin, était optimale, mais en 2016, Éric Opsomer et Nicolas Vandewalle, deux chercheurs de l'université de Liège (Belgique) ont trouvé une structure encore meilleure. Elle est composée de 24 polyèdres dont 16 à 12 faces et 8 à 16 faces. Pour trouver cette structure, les deux chercheurs ont mis au point un logiciel qui a testé des milliards de possibilités de pavage de l'espace.[1]