Cube de Bidiakis
Dans la discipline mathématique de la théorie des graphes, le cube de Bidiakis est un graphe 3-régulier qui a 12 sommets et 18 arêtes.
| Cube de Bidiakis | |
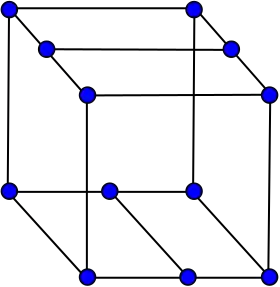 Le cube de Bidiakis construit à partir d'un cube | |
| Nombre de sommets | 12 |
|---|---|
| Nombre d'arêtes | 18 |
| Diamètre | 3 |
| Maille | 4 |
| Automorphismes | 8 () |
| Nombre chromatique | 3 |
| Indice chromatique | 3 |
| Propriétés | Cubique Hamiltonien Sans triangle Polyédrique Planaire |
Construction
Le cube de Bidiakis est un graphe hamiltonien cubique et peut être défini à l'aide de la notation LCF .
Le cube de Bidiakis peut également être construit à partir d'un cube en ajoutant des arêtes au travers des faces du haut et du bas pour relier les centres des côtés opposés sur chaque face. Les deux arêtes supplémentaires doivent être perpendiculaires l'une à l'autre. Avec cette construction, on voit que le cube Bidiakis est un graphe polyédrique car il peut être réalisé sous la forme d'un polyèdre convexe. Le théorème de Steinitz permet d'en déduire qu'il est un graphe planaire 3-sommet-connexe[1],[2].
Propriétés algébriques
Le cube de Bidiakis n'est pas un graphe sommet-transitif et son groupe d'automorphismes complet est isomorphe au groupe diédral d'ordre 8, le groupe de symétries d'un carré, comprenant à la fois des rotations et des symétries.
Le polynôme caractéristique du cube de Bidiakis est .
Galerie
 Le cube de Bidiakis est hamiltonien.
Le cube de Bidiakis est hamiltonien. Le cube de Bidiakis est un graphe planaire.
Le cube de Bidiakis est un graphe planaire.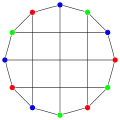 Le nombre chromatique du cube de Bidiakis vaut 3.
Le nombre chromatique du cube de Bidiakis vaut 3.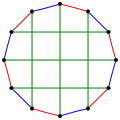 L'indice chromatique du cube de Bidiakis vaut 3.
L'indice chromatique du cube de Bidiakis vaut 3.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Bidiakis cube » (voir la liste des auteurs).
- (en) Branko Grünbaum, Volker Kaibel, Victor Klee et Günter M. Ziegler, Convex Polytopes, , 2e éd., 466 p. (ISBN 0-387-40409-0 et 978-0-387-40409-7)
- (en) Eric W. Weisstein, « Polyhedral Graph », sur MathWorld