Raisonnement par récurrence

Le triangle de Pascal extrait de son manuscrit. Par base Pascal entend une diagonale du triangle. Pascal se sert de la géométrie de son triangle pour en énoncer les propriétés. En termes modernes : les coefficients binomiaux sont définis par la relation ${\displaystyle {\binom {n+1}{p+1}}={\binom {n}{p+1}}+{\binom {n}{p}}}$ ; la conséquence XII, celle à propos de laquelle Pascal introduit la récurrence, revient à énoncer que pour tout entier p entre 1 et n, ${\displaystyle {\binom {n}{p}}={\frac {n-p+1}{p}}{\binom {n}{p-1}}}$, ce que Pascal démontre par récurrence sur n. L'étape de récurrence est exposée sur un cas particulier[3].

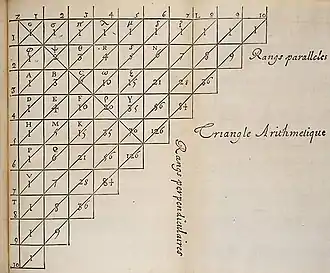
On trouve dans le Traité du triangle arithmétique de Blaise Pascal, écrit en 1654 mais publié en 1665, ce qui est généralement considéré comme la première utilisation tout à fait explicite du raisonnement par récurrence. En particulier, même si Pascal utilise parfois dans son traité des formes moins abouties, il écrit ceci[4] :

« Quoique cette proposition ait une infinité de cas, j'en donnerai une démonstration bien courte, en supposant deux lemmes.

Le premier, qui est évident de soi-même, que cette proportion se rencontre dans la seconde base; car il est bien visible, que φ est à σ comme 1 est à 1.

Le deuxième, que si cette proportion se trouve dans une base quelconque, elle se trouvera nécessairement dans la base suivante.

D'où il se voit qu'elle est nécessairement dans toutes les bases : car elle est dans la seconde base par le premier lemme ; donc par le second elle est dans la troisième base, donc dans la quatrième, et à l'infini[3]. »

Toujours au XVII^e siècle, il faut mentionner Pierre de Fermat[5] et Jacques Bernoulli[6] qui critiquent tous deux la « méthode d'induction »[7] de John Wallis, appelée depuis induction incomplète, qui correspond grossièrement à une démonstration pour les premiers entiers et « ainsi de suite ». Fermat promeut par ailleurs la méthode de descente infinie, liée elle-même à la récurrence (voir ci-dessous). Il est le premier à l'identifier et la nommer mais celle-ci est déjà utilisée, là sans ambiguïté aucune, par Euclide[8]. Bernoulli, lui, propose de démontrer le passage de n à n + 1, soit exactement le raisonnement par récurrence.

Au cours du XVIII^e et du XIX^e siècle, le raisonnement par récurrence est de plus en plus utilisé pour aboutir finalement à sa formalisation et à son axiomatisation, d'abord partiellement par Grassmann en 1861[9], puis par Richard Dedekind en 1888 et indépendamment par Giuseppe Peano en 1889[10]. Pour Dedekind il s'agit d'achever l'arithmétisation des réels, en donnant un cadre formel permettant de développer la méthode des coupures publiée en 1872[11]. Pour Peano ce sont les prémisses de son très ambitieux projet de formalisation des mathématiques (voir Formulaire de mathématiques). Dans les deux cas la récurrence n'est plus simplement un principe de démonstration reposant sur l'intuition, mais un axiome formalisant une propriété des entiers naturels.

Que Pascal soit ou non l'inventeur du raisonnement par récurrence, on ne peut négliger ses nombreux précurseurs.

Les choses se compliquent du fait de l'absence d'un langage algébrique moderne. Certains résultats ne peuvent parfois pas même être énoncés en toute généralité, et le sont donc pour des entiers donnés, alors que les idées essentielles pour la démonstration du résultat général (passage de n à n + 1) sont présentes.

Cajori 1918 la décèle dans la méthode chakravala de Bhaskara II et dans la démonstration d'Euclide de l'existence d'une infinité de nombres premiers[12].

On a découvert depuis les années 1970 plusieurs formes de raisonnement par récurrence dans les mathématiques du monde arabo-islamique, voir Rashed 1972. Ainsi, vers l'an 1000, le persan Al-Karaji (953-1029) établit la formule du binôme de Newton (en fait il n'a pas les notations qui lui permettraient de l'énoncer dans le cas général, mais les méthodes fonctionnent pour un entier arbitraire). Il calcule également la somme des cubes des n premiers entiers naturels[13], al-Samaw'al poursuit ses travaux. Ces résultats utilisent bien des formes « archaïques » de définition et de raisonnement par récurrence (comme la régression, on part d'un entier donné choisi arbitrairement, et par un procédé manifestement général, en passant de n à n – 1, on se ramène au cas initial). À peu près à la même époque, Ibn al-Haytham(953-1039) utilise le raisonnement par récurrence pour calculer la somme des cubes puis des puissances quatrièmes des n premiers entiers naturels[14]. Bien qu'il ne mentionne même pas la possibilité d'aller au-delà de la puissance 4, sa méthode, itérative, le permettrait.

Durant le Moyen Âge européen, le philosophe et mathématicien juif languedocien Levi ben Gershom (1288-1344), dit Gersonide, fait un usage systématique de la régression pour établir des résultats de combinatoire (somme des cubes, nombre de permutations…)[15].

Pascal, ou Bernoulli étaient déjà considérés au XIX^e siècle comme les pères du raisonnement par récurrence, mais ensuite, on a beaucoup cité pendant la première moitié du XX^e siècle le mathématicien italien Francesco Maurolico (1494-1575) et son ouvrage Arithmeticorum libri duo (1575)[16], ceci à la suite d'un article de Giovanni Vacca de 1909, qui influença Moritz Cantor[17] et fut traduit dans d'autres langues, par exemple en français en 1911. Pour démontrer que la somme des n premiers entiers impairs est un carré parfait, Maurolico utilise une proposition (prop. 13) qui permet le passage du cas n au cas n + 1, énonce la propriété générale (prop. 15), et en fait la démonstration pour n=1, 2, 3, 4, 5 grâce à la prop. 13, tout en concluant qu'il pourrait poursuivre ainsi jusqu'à l'infini. Selon Rashed et Freudenthal[18], il s'agirait d'une utilisation archaïque du raisonnement sans énonciation d'un principe général qui serait utilisable de manière systématique. D'autre part il apparaît, d'après la correspondance de Pascal, que celui-ci a lu Maurolico.

L'article de Freudenthal de 1953[19] montrant que Maurolico utilise dans son livre très peu de raisonnements de type récurrence (sous quelque forme que ce soit), et d'autre part, les découvertes de travaux antérieurs de Al-Karaji, ben Gershom et autres relativisent fortement son apport, ceci au point que les ouvrages généralistes d'histoire des mathématiques ne le mentionnent plus[20].

Les entiers impairs sont les entiers de la forme 2n + 1 (le premier, obtenu pour n = 0, est 1). On déduit d'une identité remarquable bien connue que 2n + 1 ajouté au carré de n donne le carré du nombre suivant : n² + 2n + 1 = (n + 1)² On va donc montrer par récurrence que la somme des n premiers entiers impairs est égale au carré de n : 1 + 3 + … + (2n – 1) = n². Bien que l'écriture précédente puisse laisser entendre que 2n – 1 > 3, on ne le supposera pas[23]. La somme est vide donc nulle si n = 0, réduite à 1 si n = 1, égale à 1 + 3 si n = 2, etc.

• initialisation : le cas n = 0 est celui où la somme est vide, elle est donc bien égale à 0² ;
• hérédité : raisonnons sur un éventuel entier n, arbitraire, mais pour lequel 1 + 3 + … + (2n – 1) = n². Puisque l'entier impair qui suit 2n – 1 est 2n + 1, on en déduit que : 1 + 3 + … + (2n – 1) + (2n + 1) = n² + 2n + 1 = (n + 1)²,c'est-à-dire que la propriété est héréditaire.

${\displaystyle (x+y)^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}y^{k}.}$

• L’initialisation ne doit pas être oubliée. Voici un exemple un peu ad hoc (et que l'on pourrait traiter à l'aide de congruences modulo 7) mais qui illustre bien ceci. On montre facilement que les propriétés « 9ⁿ – 2ⁿ est un multiple de 7 » et « 9ⁿ – 2ⁿ⁺¹ est un multiple de 7 » sont toutes deux héréditaires. Cependant, alors que la première est vraie pour tout entier naturel n, la seconde ne l'est pas car elle n’est pas initialisable : en effet, en n = 0 on a 1 – 2 = –1, qui n'est pas divisible par 7. Pour la première proposition :
  • on vérifie que si n = 0, 9⁰ – 2⁰ est bien un multiple de 7 (0 est bien un multiple de 7) ;
  • on montre que si 9ⁿ – 2ⁿ est un multiple de 7, alors 9ⁿ⁺¹ – 2ⁿ⁺¹ est un multiple de 7 :${\displaystyle {\begin{aligned}9^{n+1}-2^{n+1}&=9\times 9^{n}-2\times 2^{n}\\&=9\times \left(9^{n}-2^{n}\right)+9\times 2^{n}-2\times 2^{n}\\&=9\times \left(9^{n}-2^{n}\right)+7\times 2^{n}.\end{aligned}}}$9ⁿ⁺¹ – 2ⁿ⁺¹ est donc somme de deux multiples de 7 ; c’est bien un multiple de 7.L'hérédité de la seconde propriété est strictement analogue. Pourtant, cette propriété n'est vraie pour aucun entier puisque 9ⁿ – 2ⁿ⁺¹ est la différence de 9ⁿ – 2ⁿ (multiple de 7) et de 2ⁿ (non divisible par 7).
• L’hérédité doit être démontrée pour tout entier n supérieur ou égal au dernier n₀ pour lequel la propriété a été démontrée directement (initialisation).

Si l'on prend, par exemple, la suite ${\displaystyle u_{n}={\frac {n^{2}-n+1}{n^{2}}}}$, on peut observer que cette suite est croissante à partir de n = 2 car ${\displaystyle u_{n+1}-u_{n}={\frac {n^{2}-n-1}{n^{2}(n+1)^{2}}}>0}$. Si l'on cherche à démontrer que ${\displaystyle u_{n}\geq 1}$ pour tout ${\displaystyle n\geq 1}$ : l’initialisation est facile à prouver car ${\displaystyle u_{1}=1}$ ; l’hérédité aussi car, la suite étant croissante, si ${\displaystyle u_{n}\geq 1}$ alors ${\displaystyle u_{n+1}\geq 1}$. Pourtant cette inégalité est vraie seulement pour n = 1. L’hérédité n’a en réalité été prouvée que pour n supérieur ou égal à 2 et non pour n supérieur ou égal à 1.

Il peut arriver que, pour l'hérédité, quand il s'agit de démontrer P(n + 1), on ait besoin de supposer la propriété aux deux rangs précédents, c'est-à-dire non seulement pour n, mais aussi pour n – 1. On est amené à utiliser le principe de récurrence suivant :

Soit P(n) une propriété définie sur N, si :

• P(0)
• P(1)
• [P(n) et P(n + 1)] ⇒ P(n + 2) (pour tout n ∈ N)

alors P(n) pour tout n ∈ N.

Cette propriété est en apparence plus forte que la récurrence simple, puisque l'on a une hypothèse supplémentaire à notre disposition, mais lui est en fait équivalente, puisque cela revient à démontrer [P(n) et P(n + 1)] par récurrence simple. On trouvera par exemple dans l'article suite de Fibonacci des exemples d'application de ce principe de récurrence.

La récurrence précédente peut être généralisée à plus d'hypothèses, 3, 4, etc. Mais tous ces principes apparaissent comme des cas particuliers du principe de récurrence suivant, parfois appelé récurrence forte, qui permet, pour démontrer la propriété au rang suivant de la supposer vraie pour tous les rangs inférieurs (pour cette raison, cette forme de récurrence est aussi appelée récurrence cumulative). On a une version plus forte de l’hérédité :

Soit P(n) une propriété définie sur N, si :

• P(0)
• [∀k≤n P(k)] ⇒ P(n + 1) (pour tout n ∈ N)

alors P(n) pour tout entier n ∈ N.

L'initialisation reste identique, mais l'hérédité est modifiée. Pour démontrer la propriété au rang n + 1, on peut supposer la propriété vraie non seulement pour n mais aussi pour tous les entiers inférieurs à n.

À nouveau cette propriété, en apparence plus forte que la récurrence simple, lui est en fait équivalente. En effet cela revient à démontrer par récurrence simple la propriété « ∀k≤n P(k) », c'est-à-dire la propriété P pour tous les entiers inférieurs ou égaux à n. On utilise pour l'équivalence les propriétés qui caractérisent l'ordre sur N, à savoir que pour tout entier naturel k : k ≤ n + 1 ⇔ (k ≤ n ou k = n + 1) k ≤ 0 ⇔ k = 0. Cette récurrence peut également se décaler à partir d'un certain rang, exactement comme la récurrence simple.

Pour démontrer que tout entier naturel supérieur ou égal à 2 possède un diviseur premier (récurrence donc à partir du rang 2).

• On démontre que 2 possède un diviseur premier qui est lui-même
• Soit n un entier supérieur ou égal à 2, on suppose que tous les entiers d supérieurs ou égaux à 2 et inférieurs ou égaux à n possèdent un diviseur premier (hypothèse de récurrence) et l'on cherche à prouver qu’il en est de même pour n + 1.

ou bien n + 1 est premier alors il possède un diviseur premier qui est lui-même ou bien n + 1 est composé et il existe un entier d supérieur ou égal à 2 et inférieur ou égal à n qui divise n + 1. Alors, par hypothèse de récurrence, d possède un diviseur premier, qui est aussi diviseur de n + 1. Le raisonnement qui est fait pour n + 1 fonctionne tout aussi bien pour 2 : on voit sur l'exemple qu'il n'est pas vraiment nécessaire de traiter à part l'initialisation, c'est-à-dire que cette démonstration se fait plus élégamment par récurrence bien fondée ou en utilisant le principe du bon ordre (voir ci-dessous).

De façon alternative à la récurrence, en particulier la récurrence forte, on peut utiliser le principe suivant : Tout sous-ensemble non vide de N a un plus petit élément (N est bien ordonné). Par exemple, si l'on reprend l'exemple traité au paragraphe précédent, l'existence pour tout nombre d'un diviseur premier[24], on choisit directement p le plus petit diviseur différent de 1 d'un nombre n donné supérieur ou égal à 2, qui est le plus petit élément de l'ensemble non vide des diviseurs différents de 1 de n. On montre alors par l'absurde que p est premier : si p avait un diviseur strictement inférieur à p et différent de 1, il diviserait également n, et p ne serait pas le plus petit diviseur de n.

Cette propriété est une propriété de la relation d'ordre sur N. Un tel ordre est appelé bon ordre, et l'on dit que N est bien ordonné.

La propriété de récurrence se déduit de celle de bon ordre, et du fait que tout entier est soit 0, soit un successeur (de la forme n + 1).

En effet, pour une propriété P héréditaire (P(n) ⇒ P(n + 1)) et vérifiée en 0, il suffit de considérer le minimum de l'ensemble des entiers ne vérifiant pas celle-ci. Il existe dès que cet ensemble est non vide. Grâce à l'initialisation, on sait que ce minimum n'est pas 0 . Grâce à l'hérédité, on sait que ce minimum n'est pas le successeur n + 1 d'un entier n qui vérifierait la propriété P. Par conséquent, l'ensemble des entiers ne vérifiant pas P ne possède pas de minimum, il est donc vide : tout entier vérifie P.

Réciproquement, la propriété de bon ordre se déduit de la propriété de récurrence (et des propriétés de l'ordre). La contraposée de la propriété de bon ordre se déduit en effet directement de la récurrence forte (en utilisant les propriétés caractérisant l'ordre sur N). On suppose qu'un ensemble E d'entiers,n n'a pas de plus petit élément, et l'on doit montrer que E est vide, soit pour tout entier n, n ∉ E :

• 0 ∉ E (car sinon 0 serait le plus petit élément de E) ;
• on suppose pour tout entier k ≤ n, k ∉ E. Alors n + 1 ∉ E, car sinon il serait le plus petit élément de E.

Une fois admises certaines propriétés des entiers naturels (en particulier que tout entier est 0 ou le successeur d'un autre entier), on a donc équivalence entre principe de récurrence et propriété de bon ordre.

Un autre principe proche de la récurrence, en particulier de la récurrence forte, est le principe de descente infinie illustré par Pierre de Fermat : il n'existe pas de suite infinie strictement décroissante d'entiers naturels. Fermat démontre ainsi par l'absurde des résultats d'inexistence de solutions à certaines équations diophantiennes, en construisant à partir d'une solution supposée une autre solution strictement plus petite.

C'est une conséquence directe de la propriété de bon ordre, si telle suite existait, l'ensemble non vide de ses valeurs n'aurait pas de minimum. Le principe de descente infinie est directement lié à la notion de relation bien fondée, abordée dans le paragraphe suivant, dont il fournit une caractérisation.

On peut réénoncer la récurrence forte en utilisant la seule relation d'ordre, et les deux hypothèses de récurrence peuvent alors se rassembler en une seule.

Soit P(n) une propriété définie sur N, si [∀k < n P(k)] ⇒ P(n) (pour tout n ∈ N) alors P(n) pour tout n ∈ N.

Dans le cas où n = 0, l'hypothèse est vraie par vacuité de l'ensemble des k < 0, ainsi la quantification est vraie et l'assertion revient à P(0). Donc quand on prend pour < l'ordre naturel sur les entiers[25], on distingue suivant que n = 0 ou n est un « successeur », c'est-à-dire n est de la forme m + 1, on retrouve exactement la propriété de récurrence forte ci-dessus.

Cette forme du raisonnement par récurrence ne fait plus référence à la constante 0 et à l'opération successeur des entiers. Elle se généralise directement à n'importe quel ordre bien fondé non nécessairement total (et même à n'importe quelle relation bien fondée).

En effet, dire que la relation d'ordre strict sur N est bien fondée signifie que toute partie non vide de N possède un élément minimal (donc ici minimum, puisque l'ordre sur N est total), or on démontre aisément (cf. article détaillé) que cette propriété équivaut à la récurrence bien fondée. La démonstration est en fait essentiellement celle donnée ci-dessus entre récurrence et bon ordre via la récurrence forte. Mais comme il existe des bons ordres qui ne sont pas isomorphes à l'ordre usuel sur N, on a forcément utilisé au passage une propriété spécifique des entiers, en l'occurrence le fait que tout entier non nul est le successeur d'un autre entier. Cette dernière propriété est d'ailleurs une conséquence de la propriété de récurrence simple (le cas très particulier où l'on n'utilise pas l'hypothèse de récurrence). Elle n'est pas nécessairement vraie dans les ensembles bien ordonnés.

Dans son opuscule sur la fonction gamma[26], Emil Artin utilise, pour étendre à tous les isobarycentres l'inégalité de convexité pour les milieux, un principe de récurrence qui s'adapte bien au cas où la propriété se démontre facilement pour les puissances de 2. Ce principe[27] avait déjà été utilisé par Cauchy pour démontrer l'inégalité arithmético-géométrique ${\displaystyle (x_{1}x_{2}\dots x_{n})^{1/n}\leq (x_{1}+x_{2}+\cdots +x_{n})/n}$. Son énoncé est le suivant :

Soit P(n) une propriété définie sur N :

• si P(1),
• si pour tout n ∈ N, P(n) ⇒ P(2n),
• et si pour tout n ∈ N, P(n + 1) ⇒ P(n),

alors, pour tout entier n ∈ N, P(n).

L'originalité de cette méthode repose sur un principe de récurrence à rebours : on ne prouve plus une propriété de n à n + 1 mais de n + 1 à n, en y adjoignant que si la propriété est vraie d'un entier alors elle est vraie pour un autre entier strictement plus grand, ce qui donne une preuve de la propriété sur tous les entiers « en zigzag ».

Ainsi, les hypothèses P(0) et P héréditaire : ∀n [P(n) ⇒ P(n + 1)] permettent de montrer que, pour tout entier n donné, on a ${\displaystyle \vdash P(n)}$ (où le symbole ${\displaystyle \vdash }$ indique qu'il existe une démonstration de la proposition énoncée). Mais ces hypothèses seules ne permettent pas d'affirmer ${\displaystyle \vdash \forall n,P(n)}$, qui est beaucoup plus fort. C'est le principe de récurrence qui le permet.

En effet on peut avoir une théorie T, cohérente, telle que :

• 1/ Pour tout entier n, ${\displaystyle {\rm {T}}\vdash P(n)}$, (donc ${\displaystyle {\rm {T}}\vdash P(0)}$, ${\displaystyle {\rm {T}}\vdash P(1)}$, ${\displaystyle {\rm {T}}\vdash P(2)}$, ${\displaystyle {\rm {T}}\vdash P(3)}$, ...),

Sans que pourtant on ait :

• 2/ ${\displaystyle {\rm {T}}\vdash \forall n,P(n)}$.

Ceci peut se concevoir aisément par un exemple[30] : On ignore actuellement si la conjecture de Goldbach disant que tout entier pair > 2 est somme de 2 nombres premiers est un énoncé :

• indécidable de la théorie arithmétique, notée AP, mais
• effectivement vrai (et donc potentiellement démontrable dans une théorie toujours arithmétiquement correcte mais plus forte, telle que, présume-t-on, la théorie des ensembles usuelle).

Si tel est le cas, en prenant pour P(n), « 2n + 4 est somme de 2 nombres premiers », on aurait, pour tout entier n :

• ${\displaystyle {\rm {AP}}\vdash P(n)}$ car pour tout nombre pair donné, on pourrait prouver en un nombre fini d'étapes, dans AP qu'il est somme de 2 nombres premiers s'il l'est. Il suffirait pour cela de calculer les sommes des couples de nombres premiers inférieurs à n et de les comparer à n.

Mais pas :

• ${\displaystyle {\rm {AP}}\vdash \forall n,P(n)}$, dans le cas où la conjecture de Goldbach serait indécidable dans AP.

On peut même avoir une théorie T, cohérente, telle que :

• 1/ Pour tout entier n, ${\displaystyle {\rm {T}}\vdash P(n)}$, et :
• 3/ ${\displaystyle {\rm {T}}\vdash {\rm {non}}(\forall n,P(n))}$.

Une telle théorie est dite simplement cohérente et ω-incohérente (lire omega-incohérente)[31].

Ceci se conçoit toujours aisément en reprenant l'exemple ci-dessus :

• Si la proposition "∀n P(n)" (ici, la conjecture de Goldbach) est indécidable dans notre théorie (ici, AP), l'adjonction de "non [∀n P(n)]" aux axiomes de la théorie 1/ la laisse cohérente si elle l'était et préserve les théorèmes de T. Par ailleurs on a évidemment :
• ${\displaystyle {\rm {T}}\cup \{{\rm {non}}(\forall n,P(n))\}\vdash {\rm {non}}(\forall n,P(n))}$

et en remplaçant dans le paragraphe précédent T par ${\displaystyle {\rm {T'}}={\rm {T}}\cup \{{\rm {non}}(\forall n,P(n))\}}$, on a le résultat attendu.

Ainsi, il ne suffit pas de démontrer que pour tout n, P(n) [soit P(0), P(1), P(2), ...] pour démontrer ∀n P(n), comme arrive à le faire le principe de récurrence.

Une théorie dans laquelle pour tout prédicat P, pour tout n, ${\displaystyle {\rm {T}}\vdash P(n)}$ implique ${\displaystyle T\vdash \forall nP(n)}$ est dite ω-cohérente[32].