Design combinatoire

Le plan de Fano.

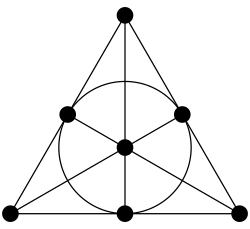
Étant donné un certain nombre n de personnes, on se demande s'il est-il possible de les affecter à des ensembles de telle manière que chaque personne figure dans au moins un ensemble, chaque paire de personnes figure dans exactement un ensemble, deux ensembles quelconques ont exactement une personne en commun, et de plus aucun ensemble ne contient toutes les personnes, ni toutes les personnes sauf une, ni exactement une personne?

La réponse à la question dépend du nombre n de personnes impliquées. Pour que le problème ait une solution, n doit être de la forme n = q ² + q + 1, mais il n'est pas certain que cette condition soit suffisante : il n'est pas simple de prouver qu'une solution existe si q est la puissance d'un nombre premier. On conjecture que ce sont les seules solutions. Il a en outre été démontré que s'il existe une solution pour q congruent à 1 ou 2 mod 4, alors q est une somme de deux carrés parfaits. Ce dernier résultat, la version faible du théorème de Bruck-Ryser-Chowla, est prouvé par une combinaison de méthodes constructives basées sur des corps finis et une application de propriétés de formes quadratiques.

Lorsqu'une telle structure existe, elle est appelée un plan projectif fini; cet exemple illustre aussi la façon dont géométrie finie et la combinatoire interagissent. Quand q = 2, le plan projectif est appelé le plan de Fano.

Le design combinatoire remonte à l'Antiquité, avec le carré de Luo Shu qui est un des premiers carrés magiques. L'une des premières applications des designs combinatoires que l'on peut dater se trouve en Inde dans le livre Brhat Samhita (la "Grande collection") écrit par le mathématicien Varahamihira vers 587 après J.-C., dans le but de créer des parfums en utilisant 4 substances sélectionnées parmi 16 substances différentes à l'aide d'un carré magique[2].

Le design combinatoire s'est développé parallèlement à la croissance générale de la combinatoire au XVII^e siècle, par exemple avec les carrés latins au XVII^e siècle et les systèmes de Steiner au XIX^e siècle. Le design combinatoire a également été populaire dans les mathématiques récréatives, comme le problème des écolières de Kirkman (1850), et dans des problèmes pratiques, comme la programmation des tournois toutes rondes (dont la solution est publiée dans les années 1880). Au XX^e siècle, des designs ont été utilisés à les plans d'expériences, notamment les carrés latins, la géométrie finie et les schémas d'association, ouvrant le domaine des statistiques algébriques.

Une vue d'ensemble des plans en blocs partiellement équilibrés a été donné en 1965 par R. Guérin[3]. Un cours sur les plans d'expériences est celui de Philippe Besse à l'Insa de Toulouse[4].

Le domaine principal des designs combinatoire comprend les plans en blocs incomplets équilibrés (abrégé en BIBD), les matrices Hadamard et les designs de Hadamard, les plans en blocs incomplets équilibrés symétriques, les carrés latins, les plans BIBD résolubles, les ensembles de différences et le design par paires équilibrés (abrégé en PBD)[5]. D'autres designs combinatoires sont liées ou ont été développées à partir de l'étude de ces designs fondamentales.

• Un plan en blocs incomplet équilibré (abrégé en BIBD pour balanced incomplete block design), généralement appelé simplement plan en blocs, est une collection B de b sous-ensembles (appelés blocs) d'un ensemble fini X de v éléments tels que tout élément de X est contenu dans le même nombre r de blocs, chaque bloc ayant le même nombre k d'éléments, et chaque paire d'éléments distincts apparait ensemble dans le même nombre λ de blocs. Les BIBD sont également connus sous le nom 2-plans et sont souvent appelés plans de type 2-(v, k, λ). Par exemple, lorsque λ = 1 et b = v, on retrouve un plan projectif : X est alors l'ensemble de points du plan et les blocs sont les lignes.
• Un plan en blocs incomplet symétrique équilibré (abrégé en SBIBD pour symmetric balanced incomplete block design) est un plan en blocs dans lequel v = b (le nombre de points est égal au nombre de blocs). Ils constituent la sous-classe des BIBD la plus importante et la mieux étudiée. Les plans projectifs, les biplans et les 2-designs de Hadamard sont tous des SBIBD. Ils présentent un intérêt particulier car ils sont les exemples extrémaux de l'inégalité de Fisher (qui stipule que b ≥ v).
• Un plan en blocs incomplet équilibré résoluble est un plan en blocs incomplet équilibré dont les blocs peuvent être partitionnés en ensembles, appelés classes parallèles, dont chacun constitue une partition de l'ensemble de points du BIBD. L'ensemble des classes parallèles est appelé une résolution du plan. Une solution au célèbre problème des 15 écolières de Kirkman est la résolution d'un plan en blocs incomplet équilibré avec les paramètres v = 15, k = 3 et λ = 1[6].
• Un rectangle latin est une matrice de dimension r × n, avec r ≤ n , qui a comme entrées les nombres 1, 2, 3,..., n (ou tout autre ensemble de n symboles distincts) et telle que les nombres figurant dans chaque ligne et dans chaque sont tous distincts. Un carré latin est un rectangle latin avec r = n. Si r < n, alors il est possible d'ajouter n - r lignes à un rectangle latin pour former un carré latin, en utilisant le théorème des mariages de Hall[7].

Deux carrés latins d'ordre n sont dits orthogonaux si l'ensemble des couples composés des entrées aux mêmes places dans les deux carrés a n ² membres distincts (tous les couples possibles se produisent). Un ensemble de carrés latins de même taille forme un ensemble de carrés latins mutuellement orthogonaux (abrégé en MOLS) si chaque paire de carrés latins de l'ensemble est orthogonale. Il peut y avoir au plus n - 1 carrés dans un ensemble de MOLS d'ordre n. Un ensemble de n - 1 MOLS d'ordre n peut être utilisé pour construire un plan projectif d'ordre n (et réciproquement).

• Un ensemble de différences de type (v, k, λ) est un sous-ensemble D de k éléments d'un groupe G d'ordre v, tel que chaque élément de G autre que l'identité peut s'écrire d'exactement λ façons comme produit d'éléments de D (l'opération dans G est notée multiplicativement)[8].

Si D est un ensemble de différences et g est dans G, alors g D = { gd : d dans D } est également un ensemble de différences, appelé une translation de D. L'ensemble de toutes les translations d'un ensemble de différences D forme un plan en blocs symétrique. Dans un tel plan en blocs, il y a v éléments et v blocs. Chaque bloc se compose de k points, chaque point est contenu dans k blocs. Deux blocs quelconques ont exactement λ éléments en commun et deux points quelconques apparaissent ensemble dans λ blocs. Ce plan en blocs incomplet symétrique équilibré est appelé le développement de D[9].

Dans le cas particulier où λ = 1, l'ensemble de différences est un plan projectif. Un exemple d'ensemble de différences de paramètres (7,3,1) définie dans le groupe abélien ${\displaystyle \mathbb {Z} /7\mathbb {Z} }$ (noté additivement) est formé par le sous-ensemble {1,2,4}. Le développement de cet ensemble de différences donne le plan Fano.

Étant donné que tout ensemble de différences produit un SBIBD, l'ensemble de paramètres doit satisfaire le théorème de Bruck-Ryser-Chowla, mais tous les SBIBD ne produisent pas un ensemble de différences.

• Une matrice de Hadamard d'ordre m est une matrice carrée H dont les entrées sont ± 1 telles que HH^⊤ = m I _m, où H^⊤ est la transposée de H et I_m est la matrice d'identité d'ordre m. Une matrice Hadamard peut être mise sous une forme standard dans laquelle les entrées de la première ligne et de la première colonne sont toutes égales à +1. Si l'ordre m > 2, alors m doit être un multiple de 4.

Si, dans une matrice de Hadamard d'ordre 4a en forme standard, on supprime la première ligne et la première colonne et on convertit chaque -1 à 0, la matrice 0–1 obtenue est la matrice d'incidence d'un design symétrique de paramètres 2- (4a - 1, 2a - 1, a -1) appelé 2-design de Hadamard[10]. Cette construction est réversible, et la matrice d'incidence d'un 2-design symétrique avec ces paramètres peut être utilisée pour construire une matrice de Hadamard d'ordre 4a. Quand a = 2, on obtient encore le plan de Fano, sous la forme d'un 2-design de Hadamard.

• Un design équilibré par paire (abrégé en PBD pour pairwise balanced design) est un ensemble X avec une famille de sous-ensembles de X (pas nécessairement de même taille ni nécessairement distincts) tels que toute paire d'éléments distincts de X est contenue exactement dans λ > 0 sous-ensembles. L'ensemble X peut être l'un de ces sous-ensembles, et si tous les sous-ensembles sont des copies de X, le PBD est dit trivial. La taille de X est v et le nombre de sous-ensembles dans la famille (compté avec multiplicité) est b.

L'inégalité de Fisher s'applique aux PBD[11]: pour tout PBD non trivial, on a v ≤ b.

Ce résultat généralise également le célèbre théorème de De Bruijn-Erdős : pour un PBD avec λ = 1 n'ayant pas de blocs de taille 1 ou v, on a v ≤ b, avec égalité si et seulement si le PBD est un plan projectif ou un quasi-pinceau[12].

Le Handbook of Combinatorial Designs (Colbourn et Dinitz 2007) contient 65 chapitres consacrés chacun à un design combinatoire autre que ceux déjà donnés ci-dessus. Voici un extrait de cette liste :

• Un design ternaire équilibré (abrégé en BTD pour balanced ternary design) de paramètres (V, B ; ρ₁, ρ₂, R ; K, Λ) est un arrangement de V éléments en B multiensembles (blocs), chacun de cardinalité K (K ≤ V), satisfaisant:

1. Chaque élément apparaît R = ρ₁ + 2 ρ₂ fois au total, avec multiplicité 1 dans exactement ρ₁ blocs et multiplicité 2 dans exactement ρ₂ blocs.
2. Chaque paire d'éléments distincts apparaît Λ fois (compté avec la multiplicité); autrement dit, si m_vb est la multiplicité de l'élément v dans le bloc b, alors pour chaque paire d'éléments distincts v et w, on a

${\displaystyle \sum _{b=1}^{B}m_{vb}m_{wb}=\Lambda }$.

Par exemple, l'un des deux seuls BTD de paramètres (4,8; 2,3,8; 4,6) non isomorphes est, avec les blocs représentés en colonnes[13] :

1	1	1	2	2	3	1	1
1	1	1	2	2	3	2	2
2	3	4	3	4	4	3	3
2	3	4	3	4	4	4	4

La matrice d'incidence d'un BTD (où les entrées sont les multiplicités des éléments dans les blocs) peut être utilisée pour former un code correcteur d'erreurs ternaire de façon analogue à la formation de codes binaires à partir des matrices d'incidence des BIBD[14].

• Un design de tournoi équilibré d'ordre n (abrégé en BTD (n) pour balanced tournament design) est un tableau rectangulaire de n lignes et 2n -1 colonnes contenant des paires non ordonnées distinctes d'un ensemble V à 2n éléments, tel que

1. chaque élément de V apparaît exactement une fois dans chaque colonne, et
2. chaque élément de V apparaît au plus deux fois dans chaque ligne.

Un exemple de BTD (3) est donné par

1 6	3 5	2 3	4 5	2 4
2 5	4 6	1 4	1 3	3 6
3 4	1 2	5 6	2 6	1 5

Les colonnes d'un BTD ( n ) fournissent une 1-factorisation du graphe complet K_2n à 2n sommets[15].

Les BTD ( n ) peuvent être utilisés pour planifier des tournois toutes rondes : les lignes représentent les emplacements, les colonnes les tours du jeu et les entrées sont les joueurs ou les équipes en compétition.

• Un carré de fréquence (F-carré) est une généralisation d'ordre supérieur d'un carré latin. Soit S = { s₁, s₂,..., s_m } un ensemble de symboles distincts et soit (λ₁, λ₂,..., λ_m) un vecteur fréquence d'entiers positifs. Un carré de fréquence d'ordre n est un tableau n × n dans lequel chaque symbole s _i, pour i = 1,2,..., m, apparaît λ _i fois dans chaque ligne et colonne. L' ordre du carré est n = λ₁ + λ₂ + ... + λ_m. Un F-carré est sous forme standard si dans la première ligne et la première colonne, toutes les occurrences de s_i précèdent celles de s_j lorsque i < j.

Un carré de fréquence F₁ d'ordre n basé sur l'ensemble { s₁, s₂,..., s_m } avec vecteur de fréquence ( λ₁, λ₂,..., λ_m ) et un carré de fréquence F ₂, également d'ordre n, basé sur l'ensemble {t₁, t₂,..., t_k } avec vecteur de fréquence ( μ₁, μ₂,..., μ_k ) sont dits orthogonaux si chaque couple (s_i, t_j ) apparaît précisément λ_i μ_j fois lorsque F₁ et F₂ sont superposés.

• Les systèmes triples de Hall (abrégé en HTS pour Hall triple system) sont des cas particuliers des systèmes triples de Steiner (STS) (les blocs sont ici appelés lignes) avec la propriété que la sous-structure générée par deux lignes qui se croisent est isomorphe au plan affine fini AG (2,3).

Tout espace affine AG (n, 3) est un exemple de système de Hall triple. Un tel HTS est lui-même dit affine. Il existe des HTS qui ne sont pas affines.

Le nombre de points d'un HTS est de 3^m pour un entier m ≥ 2. Des HTS non affinés existent pour tout m ≥ 4 et n'existent pas pour m = 2 ou 3[16].

Chaque système triple de Steiner est équivalent à un quasigroupe de Steiner (qui est idempotent, commutatif et satisfaisant (xy)y = x pour tout x et y ). Un système triple de Hall est équivalent à un quasigroupe de Steiner qui de plus est distributif, c'est-à-dire qui satisfait a(xy) = (ax)(ay) pour tout a, x, y dans le quasigroupe[17].

• Un design de Howell H (s, 2n) sur ensemble symboles S de 2n éléments est un tableau de taille s × s tel que:

1. Chaque cellule du tableau est soit vide, soit contient une paire non ordonnée de S ,
2. Chaque symbole apparaît exactement une fois dans chaque ligne et colonne du tableau, et
3. Chaque paire non ordonnée de symboles apparaît dans au plus une cellule du tableau.

Un exemple de design de Howell H (4,6) est

0 4		1 3	2 5
2 3	1 4	0 5
	3 5	2 4	0 1
1 5	0 2		3 4

Un design H (2n -1, 2n ) est un carré de Room de côté 2n - 1, et les designs de Howell généralisent donc la notion de carré de Room.

Les paires de symboles dans les cellules d'un design de Howell peuvent être vues comme les arêtes d'un graphe s-régulier à 2 n sommets, appelé le graphe sous-jacent du design de Howell.

Les designs de Howell cycliques sont utilisées comme des mouvements de Howell dans les tournois de bridge en double. Les lignes du design représentent les tours, les colonnes représentent les planches et les diagonales représentent les tables[18].

• Un design de loto de paramètres (n, k, p, t) est un ensemble V de n éléments et un d'ensemble β de sous-ensembles à k éléments de V (les blocs) de sorte que, pour tout sous-ensemble P à p éléments de V, il existe un bloc B dans β pour lequel |P ∩ B| ≥ t. On note L(n, k, p, t) le plus petit nombre de blocs dans tout design de loto de paramètres (n, k, p, t). Ci-dessous un design de loto de paramètres (7,5,4,3) avec le plus petit nombre possible de blocs[19] :

{1,2,3,4,7} {1,2,5,6,7} {3,4,5,6,7}.

Les design de loto modélisent une loterie qui se déroule de la manière suivante: Les individus achètent des billets composés de k nombres choisis parmi un ensemble de n nombres. Après la vente des billets, un ensemble de p nombres est sélectionné au hasard parmi les n nombres. Ce sont les numéros gagnants. Tout billet vendu qui contient t ou plus de numéros gagnants donne droit à un prix. Des prix plus importants vont aux billets avec plus de nombres gagnants. La valeur de L( n, k, p, t ) intéresse à la fois les joueurs et les chercheurs, car il s'agit du plus petit nombre de billets à acheter pour être certain de recevoir un prix.

La loterie hongroise est un modèle de loterie de paramètres (90,5,5, t ), et on sait que L(90,5,5,2) = 100. Les loteries avec paramètres (49,6,6, t ) sont également populaires dans le monde entier et on a L(49,6,6,2) = 19. En général cependant, ces chiffres sont difficiles à calculer et ne sont pas connus[20].

Une construction géométrique d'un tel design est donnée dans la loterie de Transylvanie.

• Un design de Mendelsohn de paramètres (v, k, λ), (abrégé en MD(v, k, λ) pour Mendelsohn design) est un ensemble V à v éléments et une collection β de k-uplets ordonnés d'éléments distincts de V (appelés les blocs), qui ont la propriété que chaque la couple (x,y) d'éléments de V avec x ≠ y est cycliquement adjacente dans λ blocs. Le couple (x, y) d'éléments distincts est dit cycliquement adjacente dans un bloc si les éléments apparaissent soit consécutivement (..., x, y...) soit (y,..., x) avec y en premier et x en dernier élément.

• Un système triple de Mendelsohn est un design MD(v, 3, λ) où k=3 ; il est noté plus simplement MTS(v, λ). Un exemple de MTS (4,1) sur V = {0,1,2,3} est:

(0,1,2) (1,0,3) (2,1,3) (0,2,3)

Tout système triple peut être transformé en un système triple de Mendelson en remplaçant le triplet non ordonné {a, b, c} par la paire de triplets ordonnés (a, b, c) et (a, c, b), mais comme le montre l'exemple, la réciproque de cette opération n'est pas valable.

Si (Q, ∗) est un quasigroupe semi-symétrique idempotent, c'est-à-dire si x ∗ x = x (idempotence) et x ∗ ( y ∗ x ) = y (semi-symétrie) pour tout x, y dans Q, posons β = {(x, y, x ∗ y ): x, y dans Q }. Alors ( Q, β) est un système triple de Mendelsohn MTS (|Q |, 1). Cette construction est réversible[21].

• Un quasi-3 design est un design symétrique (abrégé en SBIBD) dans lequel chaque triple de blocs s'intersecte en x ou y points, pour deux entiers x et y fixes appelés les nombres de triple intersection (avec par exemple x<y). Tout design symétrique avec λ≤ 2 est un quasi-3 plan pour x=0 et y=1. Le design point-hyperplan de géométrie projective de type |PG(n,q) est un quasi-3 design avec x=(q^{n −2}-1)/(q-1) et y=λ=(q^{n -1}-1)/(q-1). Si y=λ pour un quasi-3 plan, le plan est isomorphe à PG(n,q) ou à un plan projectif[22].
• Un plan quasi symétrique D de paramètres t-(v,k,λ) est un plan avec les nombres d'intersection x et y (x<y) si deux blocs distincts s'intersectent en x ou y points. Ces plans se présentent naturellement dans l'étude des plans duaux avec λ=1. Un plan non symétrique de paramètres 2-(v,k,1) avec b>v est quasi-symétrique pour x=0 et y=1. Un multiple d'un plan symétrique de paramètres 2-(v, k, λ), obtenu en répétant tous les blocs un certain nombre de fois, est quasi-symétrique avec x = λ et y = k. Les 3-designs de Hadamard (une extension des 2-designs de Hadamard) sont quasisymétriques[23].

Tout plan en blocs quasi-symétrique donne lieu à un graphe fortement régulier (en tant que graphe de blocs), mais tous les graphes fortement réguliers ne se présentent pas de cette façon[24].

La matrice d'incidence d'un design quasisymmetric de paramètres 2-(v, k, λ) avec k ≡ x≡ y (mod 2) génère un code binaire auto-orthogonal (lorsqu'il est bordé quand k est impair)[25].

• Un design sphérique est un ensemble fini X de points d'une sphère de diùmension (d - 1) tel que, pour un certain entier t, la valeur moyenne sur X de chaque polynôme

${\displaystyle f(x_{1},\ldots ,x_{d})\ }$

de degré total au plus t est égale à la valeur moyenne de f sur toute la sphère, c'est-à-dire l'intégrale de f divisée par l'aire de la sphère.

• Un rectangle k-toscan de dimension r x n sur n symboles est un rectangle à r lignes et n colonnes vérifiant :

1. chaque ligne est une permutation des n symboles et
2. pour deux symboles distincts a et b et pour chaque entier m de 1 à k, il y a au plus une ligne dans laquelle b est à m pas à droite de a.

Si r = n et k = 1, ces rectangles sont appelés carrés toscans, tandis que si r = n et k = n - 1, ce sont des carrés florentins. Un carré romain est un carré toscan qui est également un carré latin (ceux-ci sont également connus sous le nom de carrés latins complets en ligne). Un carré du Vatican est une carré florentin qui est aussi un carré latin.

L'exemple suivant est un carré 1-toscan sur 7 symboles qui n'est pas 2-toscan[26] :

6	1	5	2	4	3	7
2	6	3	5	4	7	1
5	7	2	3	1	4	6
4	2	5	1	6	7	3
3	6	2	1	7	4	5
1	3	2	7	5	6	4
7	6	5	3	4	1	2

Un carré toscan sur n symboles équivaut à une décomposition du graphe complet à n sommets en n chemins orientés hamiltoniens[27].

Dans une séquence d'impressions visuelles, une carte flash peut avoir un certain effet sur l'impression donnée par la suivante. Ce biais peut être annulé en utilisant n séquences correspondant aux lignes d'un carré d'ordre n 1-toscan[28].

• Un design équilibrée en t (abrégé en t-BD) de paramètres t-(v, K, λ) est un ensemble X de v éléments avec une famille de sous-ensembles de X (appelés blocs ) dont les tailles sont dans l'ensemble K, de sorte que chaque sous-ensemble de taille t d'éléments de X est contenu dans exactement λ des blocs. Si K est un ensemble d'entiers positifs compris strictement entre t et v, alors le t-BD est dit propre. Si tous les sous-ensembles de X de taille k pour certains k sont des blocs, le t-BD est un design trivial[29].

Dans l'exemple suivant d'un design 3-{12, {4,6}, 1) sur l'ensemble X = {1,2,..., 12}, certaines paires apparaissent quatre fois (telles que 1, 2) alors que d'autres apparaissent cinq fois (6,12 par exemple)[30].

1 2 3 4 5 6 1 2 7 8 1 2 9 11 1 2 10 12 3 5 7 8 3 5 9 11 3 5 10 12 4 6 7 8 4 6 9 11 4 6 10 12

7 8 9 10 11 12 2 3 8 9 2 3 10 7 2 3 11 12 4 1 8 9 4 1 10 7 4 1 11 12 5 6 8 9 5 6 10 7 5 6 11 12

3 4 9 10 3 4 11 8 3 4 7 12 5 2 9 10 5 2 11 8 5 2 7 12 1 6 9 10 1 6 11 8 1 6 7 12

4 5 10 11 4 5 7 9 4 5 8 12 1 3 10 11 1 3 7 9 1 3 8 12 2 6 10 11 2 6 7 9 2 6 8 12

5 1 11 7 5 1 8 10 5 1 9 12 2 4 11 7 2 4 8 10 2 4 9 12 3 6 11 7 3 6 8 10 3 6 9 12

• Un carré de Youden est un tableau rectangulaire k × v (k < v) de symboles tel que chaque symbole apparaît exactement une fois dans chaque ligne et les symboles apparaissant dans une colonne forment un bloc d'un design symétrique (v, k, λ), et dont tous les blocs sont formés de cette manière. Un carré Youden est un rectangle latin. Le terme « carré » dans le nom vient d'une ancienne définition qui utilisait un tableau carré[31]. Un exemple de carré Youden 4 × 7 est donné par:

1	2	3	4	5	6	7
2	3	4	5	6	7	1
3	4	5	6	7	1	2
5	6	7	1	2	3	4

Les sept blocs (colonnes) forment un biplan d'ordre 2 (un design symétrique de paramètres (7,4,2)).

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « combinatorial design » (voir la liste des auteurs).

• E.F. Assmus et J.D. Key, Designs and Their Codes, Cambridge, Cambridge University Press, 1992 (ISBN 0-521-41361-3)
• Vasanti N. Bhat et S. S. Shrikhande, « Non-isomorphic solutions of some balanced incomplete block designs I », Journal of Combinatorial Theory, vol. 9,‎ 1970, p. 174-191 (Math Reviews 0266771)
• Thomas Beth, Dieter Jungnickel et Hanfried Lenz, Design Theory, Cambridge, Cambridge University Press, 1999, 2^e éd. (ISBN 978-0-521-44432-3).
• R. C. Bose, « A Note on Fisher's Inequality for Balanced Incomplete Block Designs », Annals of Mathematical Statistics, vol. 20, n^o 4,‎ 1949, p. 619–620. (DOI 10.1214/aoms/1177729958., lire en ligne)
• Tadeusz Caliński et Sanpei Kageyama, Block designs: A Randomization approach, vol. II : Design, New York, Springer-Verlag, coll. « Lecture Notes in Statistics » (n^o 170), 2003 (ISBN 0-387-95470-8, présentation en ligne)
• Charles J. Colbourn et Jeffrey H. Dinitz, Handbook of Combinatorial Designs, Boca Raton, Chapman & Hall/ CRC, 2007, 2^e éd. (ISBN 1-58488-506-8, présentation en ligne)
• R. A. Fisher, « An examination of the different possible solutions of a problem in incomplete blocks », Annals of Eugenics, vol. 10,‎ 1940, p. 52–75 (DOI 10.1111/j.1469-1809.1940.tb02237.x, hdl 2440/15239 )
• R. Guérin, « Vue d'ensemble sur les plans en blocs incomplets équilibrés et partiellement équilibrés », Revue de l'Institut International de Statistique, vol. 33, n^o 1,‎ 1965, p. 24-58 (ISSN 0373-1138, DOI 10.2307/1401306, JSTOR 1401306)

• Marshall Hall, Jr., Combinatorial Theory, New York, Wiley-Interscience, 1986, 2^e éd. (ISBN 0-471-09138-3)
• D.R. Hughes et E.C. Piper, Design theory, Cambridge, Cambridge University Press, 1985 (ISBN 0-521-25754-9, présentation en ligne)
• E. S. Lander, Symmetric Designs: An Algebraic Approach, Cambridge, Cambridge University Press, 1983
• C.C. Lindner et C.A. Rodger, Design Theory, Boca Raton, CRC Press, 1997 (ISBN 0-8493-3986-3)
• Damaraju Raghavarao, Constructions and Combinatorial Problems in Design of Experiments, New York, Dover (réimpression avec corrections de l'éditition de 1971 chez Wiley, 1988
• Damaraju Raghavarao et L.V. Padgett, Block Designs: Analysis, Combinatorics and Applications, World Scientific, 2005
• Herbert John Ryser, Combinatorial Mathematics (Carus Monograph n° 14), Mathematical Association of America, 1963, « Chapter 8: Combinatorial Designs »
• Douglas R. Stinson, Combinatorial Designs: Constructions and Analysis, New York, Springer, 2003 (ISBN 0-387-95487-2)
• Anne Penfold Street et Deborah J.Street, Combinatorics of Experimental Design, Clarendon, Oxford University Press, 1987, xiv + 400 (ISBN 0-19-853256-3)
• J.H. van Lint et R.M. Wilson, A Course in Combinatorics, Cambridge University Press, 1992.

• Peter J. Cameron, « Encyclopaedia of Design Theory », School of Mathematical Sciences, Queen Mary, University of London (consulté le 11 mai 2020).

• Fonction courbe
• Matrice de Costas
• Plan factoriel
• plan en blocs
• Carré magique
• Carré de Room
• Hypergraphe
• Conjecture de Williamson (en)
• Journal of Combinatorial Designs

• Portail des mathématiques