Ergosphère

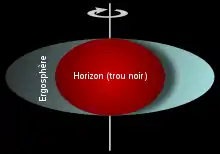
En astrophysique, l'ergorégion est une région comprise entre l'horizon et l'ergosphère d'un trou noir en rotation (trou noir de Kerr ou trou noir de Kerr-Newman). Pour de tels objets, la rotation du trou noir a tendance à entraîner l'espace et la matière dans son mouvement. Ce phénomène est appelé effet Lense-Thirring. Il prend une amplitude telle au voisinage d'un trou noir qu'il devient impossible à un observateur de rester immobile par rapport à des étoiles lointaines (considérées comme fixes). La région dans laquelle cet effet d'entraînement se produit est appelé ergosphère.

Le nom d'ergosphère (en grec, ergon signifie « travail ») vient du fait qu'il est possible d'extraire de l'énergie d'un trou noir en effectuant certaines manipulations dans l'ergosphère. On parle de processus de Penrose ou de superradiance selon que ces manipulations concernent des particules ou des ondes électromagnétiques.

Contrairement à ce que son nom indique, l'ergosphère n'est pas une région sphérique. Sa forme exacte est en fait difficilement représentable dans un espace euclidien tridimensionnel classique, en raison des distorsions de l'espace causées par le champ gravitationnel du trou noir.

Ergorégion

L'ergorégion[1]^,[2]^,[3] est une région de l'espace-temps qui s'étend depuis l'ergosphère jusqu'à l'horizon des événements d'un trou noir de Kerr[4] ou d'un autre trou noir stationnaire et axisymétrique[5].

Rayon de l'ergosphère

À $t$ fixé, l'ergosphère d'un trou noir de Kerr est une surface définie par[6] :

r=R\left(\theta \right)

,

avec[6]^,[7] :

R\left(\theta \right)={\frac {GM}{c^{2}}}\left[1+{\sqrt {1-\left({\frac {cJ}{GM^{2}}}\cos \theta \right)^{2}}}\;\right]

,

où :

$M$ est la masse[7] du trou noir ;
$J$ est son moment cinétique[7] ;
$G$ est la constante gravitationnelle ;
$c$ est la vitesse de la lumière dans le vide ;
$\theta$ est la colatitude.

Cas du trou noir de Schwarzschild

Un trou noir de Schwarzschild est, par définition, un trou noir dont le moment cinétique est nul, c'est-à-dire qui n'est pas en rotation.

Pour un tel trou noir, l'ergosphère se confond avec l'horizon des événements, de sorte qu'il n'existe pas d'ergorégion dans ce cas.

Notes et références

Gialis et Désert 2015, p. 173.
Hobson, Efstathiou et Lasenby 2009, p. 321.
Le Bellac 2015, p. 123.
Bičák 2000, p. 43.
Brito, Cardoso et Pani 2020, p. 44-45.
Gourgoulhon 2014, p. 134.
Gourgoulhon 2014, p. 131.

Voir aussi

Bibliographie

: document utilisé comme source pour la rédaction de cet article.

[Bičák 2000] (en) Jiří Bičák, « Selected solutions of Einstein's field equations : their role in general relativity and astrophysics », dans Bernd G. Schmidt (éd.), Einstein's field equations and their physical implications : selected essays in honour of Juergen Ehlers, Berlin, Heidelberg et New York, Springer, coll. « Lecture notes in physics » (n^o 540), février 2000, 1^re éd., XIII-433 p., 15,5 × 23,5 cm (ISBN 978-3-540-67073-5 et 978-3-642-08637-3, EAN 9783540670735, OCLC 490408208, BNF 44691503, DOI 10.1007/3-540-46580-4, Bibcode 2000LNP...540.....S, SUDOC 052238679, présentation en ligne, lire en ligne), chap. 1^er, p. 1-126.
[Brito, Cardoso et Pani 2020] (en) Richard Brito, Vitor Cardoso et Paolo Pani, Superradiance : new frontiers in black hole physics, Cham, Springer, coll. « Lecture notes in physics » (n^o 971), août 2020, 2^e éd. (1^re éd. juillet 2015), XXI-293 p., 15,5 × 24,5 cm (ISBN 978-3-030-46621-3, EAN 9783030466213, OCLC 1199922177, DOI 10.1007/978-3-030-46622-0, Bibcode 2020LNP...971.....B, arXiv 1501.06570, SUDOC 249662426, présentation en ligne, lire en ligne).
[Gialis et Désert 2015] Denis Gialis et François-Xavier Désert, Relativité générale et astrophysique : problèmes et exercices corrigés, Les Ulis, EDP Sciences, coll. « Grenoble Sciences », novembre 2015, 1^re éd., X-353 p., 17 × 24 cm (ISBN 978-2-7598-1749-8, EAN 9782759817498, OCLC 920911577, BNF 44394347, DOI 10.1051/978-2-7598-1896-9, SUDOC 188192891, présentation en ligne, lire en ligne).
[Gourgoulhon 2014] Éric Gourgoulhon, Relativité générale (cours d'introduction à la relativité générale), Paris, observatoire de Paris, juin 2014, 341 p. (présentation en ligne, lire en ligne [PDF]).
[Hobson, Efstathiou et Lasenby 2009] Michael Paul Hobson, George Efstathiou et Anthony N. Lasenby (trad. de l'anglais par Loïc Villain, révision scientifique par Richard Taillet), Relativité générale [« General relativity : an introduction for physicists »], Bruxelles, De Boeck Université, hors coll., décembre 2009, 1^re éd., XX-554 p., ill., 28 cm (EAN 9782804101268, OCLC 690272413, BNF 42142174, SUDOC 140535705, présentation en ligne, lire en ligne).
[Le Bellac 2015] Michel Le Bellac (préf. Thibault Damour), Les relativités : espace, temps, gravitation, Les Ulis, EDP Sciences, coll. « Une introduction à », avril 2015, 1^re éd., XIV-218 p., ill., 24 cm (ISBN 978-2-7598-1294-3, EAN 9782759812943, OCLC 910332402, BNF 44362603, SUDOC 185764118, présentation en ligne, lire en ligne).
[Taillet, Villain et Febvre 2018] Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, Louvain-la-Neuve, De Boeck Supérieur, hors coll., janvier 2018, 4^e éd. (1^re éd. mai 2008), X-956 p., ill. et fig., 24 cm (EAN 9782807307445, OCLC 1022951339, SUDOC 224228161, présentation en ligne, lire en ligne), s.v.ergosphère, p. 275-276.
(en) S. W. Hawking et G. F. R. Ellis, The Large Scale Structure of Space-Time, Cambridge University Press, coll. « Cambridge Monographs on Mathematical Physics », 1975, 400 p. (ISBN 0521099064), section 5.6, pages 165 à 168.
(en) Robert M. Wald, General Relativity, University of Chicago Press, 1984, 498 p. (ISBN 0226870332), section 12.3, page 319.

Liens externes

(de) Andreas Müller, « Ergosphäre » , Lexikon der Astrophysik, Spektrum.

Portail de l’astronomie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[GialisDésert2015173-1] Gialis et Désert 2015, p. 173.

[HobsonEfstathiouLasenby2009321-2] Hobson, Efstathiou et Lasenby 2009, p. 321.

[Le_Bellac2015123-3] Le Bellac 2015, p. 123.

[Bičák200043-4] Bičák 2000, p. 43.

[BritoCardosoPani202044-45-5] Brito, Cardoso et Pani 2020, p. 44-45.

[Gourgoulhon2014134-6] Gourgoulhon 2014, p. 134.

[Gourgoulhon2014131-7] Gourgoulhon 2014, p. 131.