Fonction de von Mangoldt

La fonction de von Mangoldt, traditionnellement notée ${\displaystyle \Lambda }$, est définie sur ${\displaystyle \mathbb {N} ^{*}}$ par

${\displaystyle \Lambda (n)={\begin{cases}\ln p&{\text{si }}n=p^{k}{\text{ pour un nombre premier }}p{\mbox{ et un entier }}k\geq 1,\\0&{\text{sinon.}}\end{cases}}}$

Cette importante fonction arithmétique n'est ni multiplicative, ni additive.

Elle satisfait l'identité[1]

${\displaystyle \ln n=\sum _{d\mid n}\Lambda (d)}$ ou, ce qui est équivalent, ${\displaystyle \Lambda (n)=-\sum _{d\mid n}\mu (d)\ln(d)}$,

où les sommes sont prises sur tous les entiers naturels d qui divisent n et où ${\displaystyle \mu }$ désigne la fonction de Möbius.

La « fonction sommatoire de von Mangoldt » ${\displaystyle \psi }$, aussi connue comme la deuxième fonction de Tchebychev, est définie par

${\displaystyle \psi (x):=\sum _{p^{k}\leq x}\ln p=\sum _{n\leq x}\Lambda (n)=\sum _{p\leq x}\lfloor \log _{p}x\rfloor \ln p}$.

Von Mangoldt a fourni une preuve rigoureuse d'une formule explicite (en) pour ${\displaystyle \psi (x)\,}$, impliquant une somme sur les zéros non triviaux de la fonction zêta de Riemann[2]. Ce fut une partie importante de la première démonstration du théorème des nombres premiers, qui équivaut à ${\displaystyle \psi (x)\sim x\quad (x\to +\infty )}$.

La fonction de von Mangoldt joue un rôle important dans la théorie des séries de Dirichlet, en particulier la fonction zêta de Riemann. Son logarithme est

${\displaystyle \log \zeta (s)=\sum _{n=2}^{\infty }{\frac {\Lambda (n)}{\ln n}}\,{\frac {1}{n^{s}}}}$

pour ${\displaystyle \Re (s)>1}$. Sa dérivée logarithmique est donc :

${\displaystyle {\frac {\zeta ^{\prime }(s)}{\zeta (s)}}=-\sum _{n=1}^{\infty }{\frac {\Lambda (n)}{n^{s}}}}$.

Plus généralement[3], sur le demi-plan de convergence d'une série de Dirichlet ${\displaystyle F(s)=\sum _{n=1}^{\infty }{\frac {f(n)}{n^{s}}}}$, on a

${\displaystyle F'(s)=-\sum _{n=1}^{\infty }{\frac {f(n)}{n^{s}}}\ln n=-\sum _{n=1}^{\infty }{\frac {f(n)}{n^{s}}}\sum _{d\mid n}\Lambda (d)}$ et si ${\displaystyle f}$ est complètement multiplicative, on en déduit

${\displaystyle F'(s)=-F(s)\sum _{d=1}^{\infty }{\frac {f(d)\Lambda (d)}{d^{s}}}}$.

La transformation de Mellin de la fonction de Tchebychev peut être trouvée en appliquant la formule sommatoire d'Abel :

${\displaystyle {\frac {\zeta ^{\prime }(s)}{\zeta (s)}}=-s\int _{1}^{\infty }{\frac {\psi (x)}{x^{s+1}}}\,{\rm {d}}x}$

qui reste vraie pour ${\displaystyle \Re (s)>1}$.

Une série exponentielle impliquant la fonction de von Mangoldt, sommée jusqu'aux premiers ${\displaystyle 10^{9}}$ termes

L'équivalent ${\displaystyle \psi (x)\sim x}$ (voir supra) se réécrit :

${\displaystyle \sum _{n\leq x}\left(\Lambda (n)-1\right)=o(x)}$.

Hardy et Littlewood ont examiné la série[4]

${\displaystyle F(y)=\sum _{n=2}^{\infty }\left(\Lambda (n)-1\right)\mathrm {e} ^{-ny}}$.

Ils ont démontré sous l'hypothèse de Riemann que

${\displaystyle F(y)=O\left({\sqrt {\frac {1}{y}}}\right)\ (y\to 0)}$

et que

${\displaystyle F(y)=\Omega _{\pm }\left({\sqrt {\frac {1}{y}}}\right)\ (y\to 0)}$.

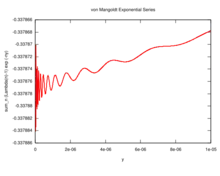
Ainsi (si l'hypothèse de Riemann est vraie) cette fonction est oscillatoire, avec des oscillations divergentes: il existe une valeur ${\displaystyle K>0}$ telle que chacune des inégalités

${\displaystyle F(y)<-{\frac {K}{\sqrt {y}}}}$ et ${\displaystyle F(z)>{\frac {K}{\sqrt {z}}}}$

est vraie infiniment souvent dans chaque voisinage de 0. Le graphe sur la droite montre que ce comportement n'est pas facile à illustrer : les oscillations ne sont clairement visibles que lorsque les 100 premiers millions de termes de la série ont été sommés, et pour ${\displaystyle y<10^{-5}}$.

La moyenne de Riesz de la fonction de von Mangoldt est donnée par

${\displaystyle \sum _{n\leq \lambda }\left(1-{\frac {n}{\lambda }}\right)^{\delta }\Lambda (n)}$

${\displaystyle =-{\frac {1}{2\pi \mathrm {i} }}\int _{c-\mathrm {i} \infty }^{c+\mathrm {i} \infty }{\frac {\Gamma (1+\delta )\Gamma (s)}{\Gamma (1+\delta +s)}}{\frac {\zeta ^{\prime }(s)}{\zeta (s)}}\lambda ^{s}ds}$

${\displaystyle ={\frac {\lambda }{1+\delta }}+\sum _{\rho }{\frac {\Gamma (1+\delta )\Gamma (\rho )}{\Gamma (1+\delta +\rho )}}+\sum _{n}c_{n}\lambda ^{-n}}$.

Ici, ${\displaystyle \lambda }$ et ${\displaystyle \delta }$ sont des nombres caractérisant la moyenne de Riesz. On doit prendre ${\displaystyle c>1}$. La somme sur ${\displaystyle \rho }$ est la somme sur les zéros de la fonction zêta de Riemann, et on peut montrer que la série ${\displaystyle \sum _{n}c_{n}\lambda ^{-n}}$ converge pour ${\displaystyle \lambda >1}$.

• Fonction de compte des nombres premiers
• Théorème de Vinogradov
• Théorème de Bombieri-Vinogradov
• Lien avec la constante d'Euler-Mascheroni

• Portail de l'analyse