Fonction signe

La fonction signe, ou signum en latin, souvent représentée sgn dans les expressions, est une fonction mathématique qui extrait le signe d'un nombre réel, c'est-à-dire que l'image d'un nombre par cette application est 1 si le nombre est strictement positif, 0 si le nombre est nul, et -1 si le nombre est strictement négatif :

\forall x\in \mathbb {R} ,\operatorname {sgn}(x)={\begin{cases}-1&{\text{si }}x<0\\0&{\text{si }}x=0\\1&{\text{si }}x>0\end{cases}}

Graphe de la fonction signe

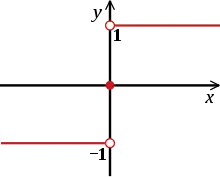
Notation alternative

La fonction signe peut également s’écrire :

\forall x\in \mathbb {R} ,\operatorname {sgn}(x)={\begin{cases}0&{\text{si }}x=0\\{\frac {x}{|x|}}{\text{ ou }}{\frac {|x|}{x}}&{\text{si }}x\neq 0\end{cases}}

On peut aussi la construire en résultat d'une limite, notamment en jouant avec les propriétés de certaines fonctions hyperboliques.

Graphe de la fonction tangente hyperbolique

En prenant $\cosh(x)$ (symétrique sur l'axe y) comme fonction de substitution pour $|x|$ , annulant sa propriété de croissance exponentielle en multipliant son inverse par $e^{x}$ et retranchant $1$ au résultat on obtient une fonction similaire à la fonction signe, passant par $0$ (figure ci à droite).

${\frac {e^{x}}{\cosh(x)}}-1={\frac {e^{2x}-1}{e^{2x}+1}}=\tanh(x)$

En analysant les limites de cette fonction en $+\infty$ , $-\infty$ et $0$ respectivement $+1$ , $-1$ et $0$ on en déduit la relation suivante:

$\operatorname {sgn}(x)=\lim _{\upsilon \rightarrow +\infty }\tanh(\upsilon x)=\lim _{\upsilon \rightarrow +\infty }{\frac {e^{\upsilon x}-1}{e^{\upsilon x}+1}}$

De façon analogue, on peut déduire des relations similaires avec ${\textstyle {\frac {2}{\pi }}tan^{-1}x}$ . Ces définitions de la fonction signe sont intéressantes car elles ne posent pas de condition sur la valeur de $x$ .

Propriétés

Tout nombre réel peut être exprimé comme le produit de sa valeur absolue et de son signe :

\forall x\in \mathbb {R} ,\,x=\operatorname {sgn}(x)|x|.

La fonction signe peut également être liée à la fonction de Heaviside :

\forall x\in \mathbb {R} ,\,\operatorname {sgn}(x)=2H(x)-1.

Continuité

Elle présente une discontinuité en 0, à la fois à gauche (puisque $\textstyle \lim _{x\to 0 \atop x<0}\operatorname {sgn}(x)=-1\neq \operatorname {sgn}(0)$ ) et à droite (puisque $\lim _{x\to 0 \atop x>0}\operatorname {sgn}(x)=1\neq \operatorname {sgn}(0)$ ).

Primitive

La fonction signe peut être vue comme la dérivée en tout réel différent de 0 de la fonction valeur absolue :

\forall x\in \mathbb {R} ^{*},\,{\frac {\mathrm {d} |x|}{\mathrm {d} x}}=\operatorname {sgn}(x).

Voir aussi

Portail de l'analyse

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.