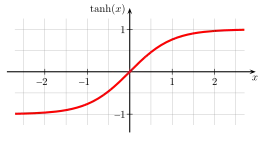
Tangente hyperbolique

La fonction tangente hyperbolique, notée tanh (ou th)[1] est la fonction complexe suivante :

${\displaystyle {\begin{matrix}\tanh$ :&\mathbb {C} \setminus {\rm {i}}\pi \left(\mathbb {Z} +{\dfrac {1}{2}}\right)&\longrightarrow &\mathbb {C} \\&z&\longmapsto &{\dfrac {\sinh(z)}{\cosh(z)}}\end{matrix}}}

où sinh est la fonction sinus hyperbolique et cosh la fonction cosinus hyperbolique.

Cette définition est analogue à celle de la fonction tangente comme rapport du sinus et du cosinus, et d'ailleurs, on a (pour tous les ${\displaystyle z}$ du domaine de définition) ${\displaystyle \tanh(z)=-i\tan(iz)}$, ou encore ${\displaystyle \tan(z)=-i\tanh(iz)}$ pour tout ${\displaystyle z\in \mathbb {C} \setminus \pi \left(\mathbb {Z} +{\frac {1}{2}}\right)}$.

La tangente hyperbolique peut s'exprimer à l'aide de la fonction exponentielle :

${\displaystyle \tanh(z)={\frac {{\rm {e}}^{z}-{\rm {e}}^{-z}}{{\rm {e}}^{z}+{\rm {e}}^{-z}}}={\frac {{\rm {e}}^{2z}-1}{{\rm {e}}^{2z}+1}}={\frac {1-{\rm {e}}^{-2z}}{1+{\rm {e}}^{-2z}}}.}$

Quelques valeurs de tanh :

• ${\displaystyle \tanh(0)=0,}$
• ${\displaystyle \tanh(1)={\frac {{\rm {e}}^{2}-1}{{\rm {e}}^{2}+1}},}$
• ${\displaystyle \tanh({\rm {i}})={\rm {i}}\tan(1).}$

La bijection réciproque de la restriction de tanh à ℝ, notée artanh (ou argtanh ou argth ou encore parfois tanh⁻¹)[2], s'explicite par :

${\displaystyle \forall x\in \left]-1,1\right[\quad \operatorname {artanh} x={\frac {1}{2}}~\ln {\frac {1+x}{1-x}}={\frac {1}{2}}\left(\ln(1+x)-\ln(1-x)\right)}$,

où ln désigne le logarithme naturel.

Plus généralement, la fonction tanh se restreint en une bijection de ℝ + i]–π/2, π/2[ dans ℂ\(]–∞, –1]∪[1, +∞[), dont la réciproque est décrite par :

${\displaystyle \forall v\in \mathbb {C} \setminus \left(]-\infty ,-1]\cup [1,+\infty [\right)\quad \operatorname {artanh} v={\frac {1}{2}}~\operatorname {Log} {\frac {1+v}{1-v}}={\frac {1}{2}}\left(\operatorname {Log} (1+v)-\operatorname {Log} (1-v)\right)}$,

où Log désigne la détermination principale du logarithme complexe.

En effet, pour tout z du domaine de définition de tanh, le complexe tanh z est l'image de u = e^2z par la fonction u ↦ v = u – 1/u + 1. Or cette fonction est une bijection de ℂ\{–1} dans ℂ\{1}, de réciproque v ↦ u = 1 + v/1 – v, et elle envoie ℂ\ℝ^– sur ℂ\(]–∞, –1]∪[1, +∞[).

La fonction artanh est holomorphe sur l'ouvert ${\displaystyle \mathbb {C} \setminus \left(]-\infty ,-1]\cup [1,+\infty [\right)}$ et admet le développement en série entière :

${\displaystyle \operatorname {artanh} z=\sum _{n=0}^{+\infty }{\frac {z^{2n+1}}{2n+1}}}$ sur le disque unité fermé ${\displaystyle |z|\leq 1}$ privé de 1 et –1.

La fonction tangente hyperbolique passe graduellement d'une valeur –1 à une valeur 1. Elle peut donc être utilisée pour représenter un phénomène de transition progressive, « douce », entre deux états.

Certains phénomènes (physiques, économiques…) ne peuvent pas être décrits par une fonction unique sur tout le domaine d'étude. C'est le cas typiquement d'un matériau subissant des changements de phase dans le domaine de température et de pression étudié. On définit alors deux domaines conjoints (ou plus), et une fonction différente sur chaque domaine ; il peut s'agir d'une fonction ayant la même forme mais des paramètres différents. On a donc une fonction de la forme

${\displaystyle f(x)={\begin{cases}f_{1}(x){\text{ pour }}x\leqslant x_{\mathrm {t} }\\f_{2}(x){\text{ pour }}x>x_{\mathrm {t} }\\\end{cases}}}$

la grandeur x_t étant une constante, la valeur frontière.

Dans certains cas, ces fonctions à gauche et à droite ne se raccordent pas parfaitement : la fonction globale n'est alors pas dérivable, voire pas continue. En particulier, si les paramètres des fonctions f₁ et f₂ sont établis par régression sur des données mesurées, il n'y a pas de raccordement par construction (f₁(x_t) ≠ f₂(x_t)). Cet effet de seuil peut conduire à des problèmes calculatoires si cette fonction est utilisée pour résoudre numériquement (par ordinateur) un problème, typiquement résolution numérique d'une équation différentielle ou bien optimisation ; on peut alors avoir une instabilité numérique, un calcul itératif qui diverge.

Fonctions de transition.

Pour résoudre ce problème, et si les fonctions f₁ et f₂ sont définies sur tout l'ensemble d'étude, on peut glisser progressivement d'une fonction à l'autre en utilisant des « fonctions de transition » construites à partir d'une tangente hyperbolique : on définit deux fonctions g₁ et g₂ de la forme

${\displaystyle {\begin{cases}g_{1}(x)=0,5\times \left[1+\tanh((x_{\mathrm {t} }-x)/l)\right]\\g_{2}(x)=0,5\times \left[1+\tanh((x-x_{\mathrm {t} })/l)\right]\\\end{cases}}}$

où l est un facteur de largeur. On définit alors la fonction globale

${\displaystyle {\tilde {f}}=g_{1}\times f_{1}+g_{2}\times f_{2}}$.

Dans le cadre de la relativité restreinte, le calcul des transformations de Lorentz fait aussi appel à la fonction tangente hyperbolique pour définir la notion de rapidité.

• (en) Eric W. Weisstein, « Hyperbolic Tangent », sur MathWorld

• Portail de l'analyse