Grand icosaèdre tronqué
En géométrie, le grand icosaèdre tronqué est un polyèdre uniforme non-convexe, indexé sous le nom U55.
Grand icosaèdre tronqué
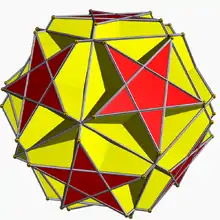
| Faces | Arêtes | Sommets |
|---|---|---|
| 32 (12{5/2}+20{6}) | 90 | 60 |
| Type | Polyèdre uniforme |
|---|---|
| Références d'indexation | U55 – C71 – W95 |
| Symbole de Wythoff | 2 5⁄2 | 3 |
| Caractéristique | 2 |
| Groupe de symétrie | Ih |
| Dual | Grand stellapentakidodécaèdre |
Ce polyèdre est la troncature du grand icosaèdre.
Coordonnées cartésiennes
Les coordonnées cartésiennes pour les sommets d'un grand icosaèdre tronqué centré à l'origine sont toutes les permutations paires de
- (±1, 0, ±3/τ)
- (±2, ±1/τ, ±1/τ3)
- (±(1+1/τ2), ±1, ±2/τ)
où τ = (1+√5)/2 est le nombre d'or (quelquefois écrit φ). En utilisant 1/τ² = 1 − 1/τ, on vérifie que tous les sommets sont sur une sphère, centrée à l'origine, avec le rayon élevé au carré égal à 10−9/τ. L'arête est de longueur 2.
Voir aussi
Lien externe
- Portail de la géométrie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.