Symbole de Wythoff

En géométrie, un symbole de Wythoff est une notation courte, créée par le mathématicien Willem Abraham Wythoff, pour nommer les polyèdres réguliers et semi-réguliers utilisant une construction kaléidoscopique, en les représentant comme des pavages sur la surface d'une sphère, sur un plan euclidien ou un plan hyperbolique.

Exemple des triangles de construction de Wythoff avec les 7 points générateurs. Les droites des miroirs actifs sont colorés en rouge, jaune et bleu avec les 3 nœuds qui leur sont opposés associés par le symbole de Wythoff.

Le symbole de Wythoff donne 3 nombres p,q,r et une barre verticale positionnelle (|) qui sépare les nombres avant et après elle. Chaque nombre représente l'ordre des miroirs à un sommet du triangle fondamental.

Chaque symbole représente un polyèdre uniforme ou un pavage, bien qu'un même polyèdre/pavage puisse avoir des symboles de Wythoff différents à partir de générateurs symétriques différents. Par exemple, le cube régulier peut être représenté par 3 | 4 2 avec une symétrie Oh et 2 4 | 2 comme un prisme carré avec deux couleurs et une symétrie D4h, autant que 2 2 2 | avec 3 couleurs et une symétrie D2h.

Tableau de résumé

Il existe 7 points générateurs avec chaque ensemble de p,q,r : (et quelques formes particulières)

Général Triangle droit (r=2)
Description Symbole
de Wythoff		 Configuration
de sommet (en)		 Symbole
de Wythoff		 Configuration
de sommet
régulier et
quasi-régulier		 q | p r (p.r)q q | p 2 pq
p | q r (q.r)p p | q 2 qp
r | p q (q.p)r 2 | p q (q.p)²
tronqué (en) et
développement (en)		 q r | p q.2p.r.2p q 2 | p q.2p.2p
p r | q p.2q.r.2q p 2 | q p.2q.2q
p q | r 2r.q.2r.p p q | 2 4.q.4.p
faces paires p q r | 2r.2q.2p p q 2 | 4.2q.2p
p q (r s) | 2p.2q.-2p.-2q p 2 (r s) | 2p.4.-2p.4/3
adouci | p q r 3.r.3.q.3.p | p q 2 3.3.q.3.p
| p q r s (4.p.4.q.4.r.4.s)/2 - -
Les 8 formes pour les constructions de Wythoff à partir d'un triangle général (p q r).

Il existe trois cas particuliers :

  • p q (r s) | - C'est un mélange de p q r | et p q s |.
  • | p q r - Les formes adoucies (alternées) donnent cet autre symbole inhabituel.
  • | p q r s - Une forme unique adoucie pour le U75 qui n'est pas constructible au sens de Wythoff.

Description

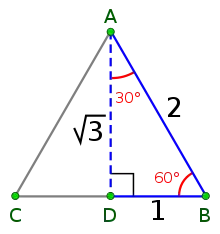
Les lettres p,q,r représentent la forme du triangle fondamental pour la symétrie, plus précisément chaque nombre est le nombre de miroirs réflexifs qui existent à chaque sommet. Sur la sphère, il existe trois types principaux de symétries : (3 3 2), (4 3 2), (5 3 2) et une famille infinie (p 2 2), pour p = 2, 3, … quelconque (toutes les familles simples ont un angle droit, donc r=2)

La position de la barre verticale dans le symbole est utilisée pour indiquer des formes spécifiques (une position de catégorie du point générateur) dans le triangle fondamental. Le point générateur peut être soit sur ou à côté de chaque miroir, activé ou non. Cette distinction engendre 8 (2³) formes possibles, négligeant une où le point générateur est sur tous les miroirs.

Dans cette notation, les miroirs sont étiquetés pr l'ordre de réflexion du sommet opposé. Les valeurs p,q,r sont listées avant la barre si le miroir correspondant est actif.

Le symbole impossible | p q r, qui implique le point générateur est sur tous les miroirs qui est le seul possible si le triangle est généré en un point. Ce symbole inusité est réassigné pour signifier quelque chose de différent. Ces symboles représentent le cas où tous les miroirs sont actifs, mais les images réfléchies énumérées de manière impaire sont ignorées. Ceci engendre des résultats de symétrie rotationnelle.

Ce symbole est fonctionnellement similaire au diagramme de Coxeter-Dynkin plus général qui montre un triangle marqué p, q, r sur les arêtes, et des cercles sur les nœuds, représentant les miroirs pour impliquer si le point générateur touchait ce miroir (le diagramme de Coxeter-Dynkin est montré comme un graphe linéaire lorsque r=2 puisqu'il n'y a pas de réflexions interagissant à travers un angle droit).

Les triangles de symétrie

Il existe 4 classes de symétrie de réflexions sur la sphère, et 2 pour le plan euclidien et une famille infinie pour le plan hyperbolique, les premières :

  1. (p 2 2) symétrie diédrique p = 2, 3, 4… (ordre 4p)
  2. (3 3 2) symétrie tétraédrique (ordre 24)
  3. (4 3 2) symétrie octaédrique (ordre 48)
  4. (5 3 2) symétrie icosaédrique (ordre 120)
  5. (4 4 2) - symétrie *442 - Triangle 45-45-90 (inclut le domaine carré (2 2 2 2))
  6. (3 3 3) - symétrie *333 - Triangle 60-60-60
  7. (6 3 2) - symétrie *632 - Triangle 30-60-90
  8. (7 3 2) - symétrie *732 (plan hyperbolique)
Sphérique diédrique Sphérique
D2h D3h Td Oh Ih
*222 *322 *332 *432 *532

(2 2 2)
(3 2 2)
(3 3 2)
(4 3 2)
(5 3 2)

Les groupes de symétrie ci-dessus incluent seulement les solutions entières sur la sphère. La liste des triangles de Schwarz (en) inclut des nombres rationnels, et détermine l'ensemble entier de solutions des polyèdres uniformes.

Plan euclidien Hyperbolique
p4m p3m p6m  
*442 *333 *632 *732

(4 4 2)
(3 3 3)
(6 3 2)
(7 3 2)

Dans les pavages ci-dessus, chaque triangle est un domaine fondamental, coloré par réflexions paires et impaires.

Résumé des pavages sphériques et plans

Une sélection des pavages créés par la construction de Wythoff sont donnés ci-dessous.

Les pavages sphériques (r=2)
(p q 2) Triangle
fondamental		 Parent Tronqué Rectifié Bitronqué Birectifié
(dual)		 Biseauté Omnitronqué
(Biseauté-tronqué)		 Adouci
Symbole de Wythoff q | p 2 2 q | p 2 | p q 2 p | q p | q 2 p q | 2 p q 2 | | p q 2
Symbole de Schläfli t0{p,q} t0,1{p,q} t1{p,q} t1,2{p,q} t2{p,q} t0,2{p,q} t0,1,2{p,q} s{p,q}
Diagramme de Coxeter-Dynkin
Figure de sommet (en) pq (q.2p.2p) (p.q.p.q) (p.2q.2q) qp (p.4.q.4) (4.2p.2q) (3.3.p.3.q)
Tetraédrique
(3 3 2)
{3,3}
(3.6.6)
(3.3a.3.3a)
(3.6.6)
{3,3}
(3a.4.3b.4)
(4.6a.6b)
(3.3.3a.3.3b)
Octaédrique
(4 3 2)
{4,3}
(3.8.8)
(3.4.3.4)
(4.6.6)
{3,4}
(3.4.4a.4)
(4.6.8)
(3.3.3a.3.4)
Icosaédrique
(5 3 2)
{5,3}
(3.10.10)
(3.5.3.5)
(5.6.6)
{3,5}
(3.4.5.4)
(4.6.10)
(3.3.3a.3.5)

Pavages planaires (r=2)

Un pavage hyperbolique représentatif est donné, et montré comme une projection du disque de Poincaré.

(p q 2) Triangle
fondamental		 Parent Tronqué Rectifié Bitronqué Birectifié
(dual)		 Biseauté Omnitronqué
(Biseauté-tronqué)		 Adouci
Symbole de Wythoff q | p 2 2 q | p 2 | p q 2 p | q p | q 2 p q | 2 p q 2 | | p q 2
Symbole de Schläfli t0{p,q} t0,1{p,q} t1{p,q} t1,2{p,q} t2{p,q} t0,2{p,q} t0,1,2{p,q} s{p,q}
Diagramme de Coxeter-Dynkin
Figure de sommet (en) pq (q.2p.2p) (p.q.p.q) (p.2q.2q) qp (p.4.q.4) (4.2p.2q) (3.3.p.3.q)
Pavage carré
(4 4 2)
{4,4}
4.8.8
4.4a.4.4a
4.8.8
{4,4}
4.4a.4b.4a
4.8.8
3.3.4a.3.4b
(Plan hyperbolique)
(5 4 2)
{5,4}
4.10.10
4.5.4.5
5.8.8
{4,5}
4.4.5.4
4.8.10
3.3.4.3.5
Pavage hexagonal
(6 3 2)
{6,3}
3.12.12
3.6.3.6
6.6.6
{3,6}
3.4.6.4
4.6.12
3.3.3.3.6
(Plan hyperbolique)
(7 3 2)
{7,3}
3.14.14
3.7.3.7
7.6.6
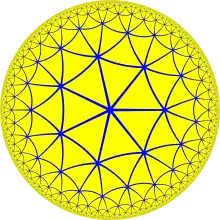{3,7}
3.4.7.4
4.6.14
3.3.3.3.7

Pavages planaires (r>2)

Le diagramme de Coxeter-Dynkin est donné dans une forme linéaire, bien que ce soit un triangle, avec le segment r trainant connecté au premier nœud.

Symbole de Wythoff
(p q r)		 Triangle
fondamental		 q | p r r q | p r | p q r p | q p | q r p q | r p q r | | p q r
Diagramme de Coxeter-Dynkin
Figure de sommet (en) (p.q)r (r.2p.q.2p) (p.r)q (q.2r.p.2r) (q.r)p (q.2r.p.2r) (r.2q.p.2q) (3.r.3.q.3.p)
Triangulaire
(3 3 3)
(3.3)3
3.6.3.6
(3.3)3
3.6.3.6
(3.3)3
3.6.3.6
6.6.6
3.3.3.3.3.3
Hyperbolique
(4 3 3)
(3.4)³
3.8.3.8
(3.4)³
3.6.4.6
(3.3)4
3.6.4.6
6.6.8
3.3.3.3.3.4

Recouvrements des pavages sphériques (r=2)

Les pavages sont montrés comme des polyèdres. Certaines de ces formes sont dégénérées, données par des accolades des figures de sommet (en), avec les arêtes ou les sommets de recouvrement.

(p q 2) Triangle
fondamental		 Parent Tronqué Rectifié Bitronqué Birectifié
(dual)		 Biseauté Omnitronqué
(Biseauté-tronqué)		 Adouci
Symbole de Wythoff q | p 2 2 q | p 2 | p q 2 p | q p | q 2 p q | 2 p q 2 | | p q 2
Symbole de Schläfli t0{p,q} t0,1{p,q} t1{p,q} t1,2{p,q} t2{p,q} t0,2{p,q} t0,1,2{p,q} s{p,q}
Diagramme de Coxeter-Dynkin
Figure de sommet (en) pq (q.2p.2p) (p.q.p.q) (p.2q.2q) qp (p.4.q.4) (4.2p.2q) (3.3.p.3.q)
Icosaédrique
(5/2 3 2)		  
{3,5/2}
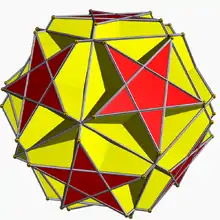(5/2.6.6)
(3.5/2)2
[3.10/2.10/2]
{5/2,3}
[3.4.5/2.4]
[4.10/2.6]
(3.3.3.3.5/2)
Icosaédrique
(5 5/2 2)		  
{5,5/2}
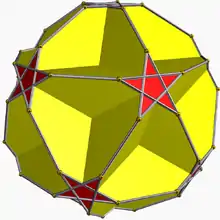(5/2.10.10)
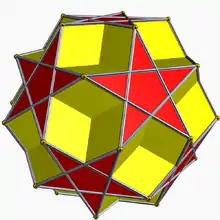(5/2.5)2
[5.10/2.10/2]
{5/2,5}
(5/2.4.5.4)
[4.10/2.10]
(3.3.5/2.3.5)

Références
  • (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Wythoff symbol » (voir la liste des auteurs).
  • (en) H. S. M. Coxeter Regular Polytopes, 3e éd, 1973,Dover (ISBN 0-486-61480-8), chap. V (The Kaleidoscope), § 5.7 (Wythoff's construction)
  • (en) H. S. M. Coxeter The Beauty of Geometry: Twelve Essays, Dover, 1999 (ISBN 0-486-40919-8), chap. 3 (Wythoff's Construction for Uniform Polytopes)
  • (en) H. S. M. Coxeter, M. S. Longuet-Higgins et J. C. P. Miller, « Uniform polyhedra », Phil. Trans., 246 A, 1954, p. 401-450.
  • (en) Magnus Wenninger, Polyhedron Models, Cambridge, Eng., CUP, , 1re éd., 228 p., poche (ISBN 978-0-521-09859-5, lire en ligne), p. 9-10.

Voir aussi

Articles connexes

Liens externes
  • Portail de la géométrie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.