Icosidodécaèdre tronqué
L'icosidodécaèdre tronqué est un solide d'Archimède. Il possède 30 faces carrées régulières, 20 faces hexagonales régulières, 12 faces décagonales régulières, 120 sommets et 180 arêtes. Puisque chacune des faces possède un centre de symétrie, le grand rhombicosidodécaèdre est un zonoèdre (à quinze générateurs).
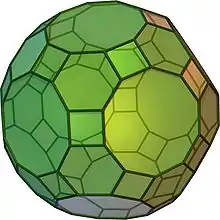
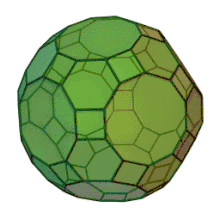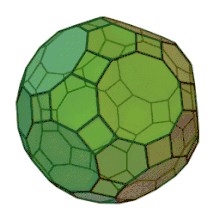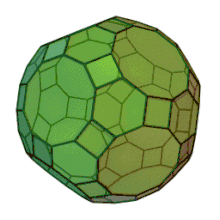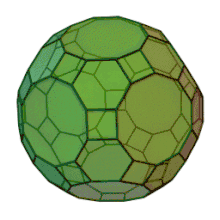
| Faces | Arêtes | Sommets |
|---|---|---|
| 62 carrés, hexagones et décagones | 180 | 120 de degré 3 |
| Type | Solide d'Archimède |
|---|---|
| Caractéristique | 2 |
| Propriétés | Zonoèdre |
| Groupe de symétrie | Ih |
| Dual | Hexaki icosaèdre |
Son dual est l'hexaki-icosaèdre, solide de Catalan.
Autres noms
D'autres noms incluent :
- grand rhombicosidodécaèdre ;
- icosidodécaèdre rhombitronqué ;
- icosidodécaèdre omnitronqué (en).
Le nom Icosidodécaèdre tronqué, donné à l'origine par Johannes Kepler est inexact. Si vous tronquez (en) un icosidodécaèdre en coupant les coins, vous n'obtenez pas cette figure uniforme : certaines faces seront des rectangles. Néanmoins, la figure résultante est topologiquement équivalente à celle-ci et peut toujours être déformée jusqu'à ce que les faces soient régulières.
Le nom grand rhombicosidodécaèdre (de même qu'icosidodécaèdre rhombitronqué) fait référence au fait que les 30 faces carrées sont placées dans les mêmes plans que les 30 faces du triacontaèdre rhombique qui est le dual de l'icosidodécaèdre. À comparer avec le petit rhombicosidodécaèdre.
Une source malheureuse de confusion : il existe un polyèdre uniforme non convexe avec le même nom : le grand rhombicosidodécaèdre uniforme.
Coordonnées cartésiennes
Les coordonnées cartésiennes pour les sommets d'un grand rhombicosidodécaèdre centré à l'origine sont toutes les permutations circulaires de
- ,
- ,
- ,
- ,
- ,
où est le nombre d'or. En utilisant , on vérifie que tous ces sommets sont sur une sphère centrée à l'origine.
Annexes
Articles connexes
Références
, dont la référence était (en) Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979 (ISBN 978-0-486-23729-9).
Liens externes
- (en) The Uniform Polyhedra sur mathconsult.ch
- (en) Virtual Polyhedra sur le site de George W. Hart (en)
- Portail de la géométrie