Icosidodécaèdre

Un icosidodécaèdre est un polyèdre à vingt faces triangulaires et douze faces pentagonales. Un icosidodécaèdre possède 30 sommets identiques, où deux triangles et deux pentagones se rencontrent, et 60 arêtes identiques qui séparent un triangle d'un pentagone. En tant que tel, c'est un solide d'Archimède et plus particulièrement, un polyèdre quasi régulier.

Icosidodécaèdre

Éléments

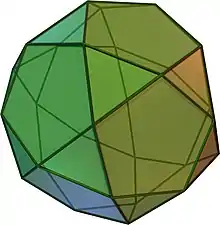
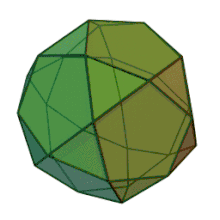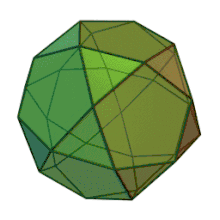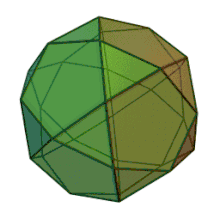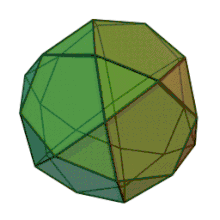
Faces	Arêtes	Sommets
32 : 20 triangles et 12 pentagones	60	30 de degré 4

Données clés

Type	Solide d'Archimède
Caractéristique	2
Propriétés	quasi régulier et convexe
Groupe de symétrie	Ih
Dual	Triacontaèdre rhombique

Patron.

On obtient ce polyèdre entre autres en tronquant un des deux solides de Platon de trente arêtes (l'icosaèdre ou le dodécaèdre) à chaque sommet, par une section qui passe par les milieux de toutes les arêtes issues du sommet tronqué. Ses soixante arêtes égales sont les côtés de six décagones réguliers convexes concentriques : six sections équatoriales du solide tronqué ou du solide initial.

Un icosidodécaèdre possède une symétrie icosaédrique, et sa première stellation est le composé d'un dodécaèdre et de son dual, l'icosaèdre, avec les sommets de l'icosaèdre localisés aux milieux des arêtes du dodécaèdre.

Des coordonnées commodes pour les 30 sommets d'un icosidodécaèdre sont les permutations circulaires de

${\displaystyle \left(0,0,\pm \varphi \right)}$

${\displaystyle \left(\pm {\tfrac {1}{2}},\pm {\tfrac {\varphi }{2}},\pm {\tfrac {(1+\varphi )}{2}}\right)}$

où ${\displaystyle \varphi ={\tfrac {1+{\sqrt {5}}}{2}}}$ est le nombre d'or. En utilisant ${\displaystyle \varphi ^{2}=\varphi +1}$, on vérifie que ces sommets sont sur une sphère centrée à l'origine.

Son polyèdre dual est le triacontaèdre rhombique. Un icosidodécaèdre peut être divisé le long de plusieurs plans pour former des rotondes décagonales, qui figurent parmi les solides de Johnson.

Dans la nomenclature standard utilisée pour les solides de Johnson, un icosidodécaèdre serait appelé une gyrobirotonde décagonale . En effet, on obtient un icosidodécaèdre en accolant deux « rotondes » décagonales par leur base, telle que leur face supérieure (les deux pentagones opposés) soient orientées différemment (c'est pourquoi l'on ajoute « gyro- »).