Graphe de Biggs-Smith

Le graphe de Biggs-Smith est, en théorie des graphes, un graphe 3-régulier possédant 102 sommets et 153 arêtes.

Graphe de Biggs-Smith

Représentation du graphe de Biggs-Smith
Nombre de sommets 102
Nombre d'arêtes 153
Rayon 7
Diamètre 7
Maille 9
Automorphismes 2 448
Nombre chromatique 3
Indice chromatique 3
Propriétés Symétrique
Distance-régulier
Cubique
Hamiltonien

Propriétés

Propriétés générales

Le diamètre du graphe de Biggs-Smith, l'excentricité maximale de ses sommets, est 7, son rayon, l'excentricité minimale de ses sommets, est 7 et sa maille, la longueur de son plus court cycle, est 9. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommet ou de 3 arêtes.

La graphe de Biggs-Smith est l'un des 13 graphes cubiques distance-réguliers[1]. Il est également hamiltonien et possède 2 849 472 cycles hamiltoniens distincts.

Coloration

Le nombre chromatique du graphe de Biggs-Smith est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.

L'indice chromatique du graphe de Biggs-Smith est 3. Il existe donc une 3-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.

Propriétés algébriques

Le graphe de Biggs-Smith est symétrique, c'est-à-dire que son groupe d'automorphismes agit transitivement sur ses arêtes, ses sommets et ses arcs. Il est donc également arête-transitif et sommet-transitif. Le graphe de Biggs-Smith est l'unique graphe cubique symétrique à 102 sommets et sa notation dans le Foster Census, le catalogue classifiant tous les graphes cubiques symétriques, est F102A[2],[3].

Le groupe d'automorphisme du graphe de Biggs-Smith est d'ordre 2 448 et est isomorphe au groupe projectif linéaire PSL(2,17)[4].

Le polynôme caractéristique de la matrice d'adjacence du graphe de Biggs-Smith est : . Le graphe de Biggs-Smith est déterminé de façon unique par son spectre de graphe, l'ensemble des valeurs propres de sa matrice d'adjacence[5].

Représentations
  • Représentation du nombre chromatique du graphe de Biggs-Smith : 3.
  • Représentation de l'indice chromatique du graphe de Biggs-Smith : 3.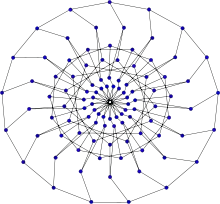
  • Représentation alternative du graphe.

Voir aussi

Liens internes

Liens externes

Références
  1. (en) A. E. Brouwer, A. M. Cohen et A. Neumaier, Distance-Regular Graphs. New York: Springer-Verlag, 1989
  2. (en) Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41-63, 2002
  3. (en) Royle, G. "Cubic Symmetric Graphs (The Foster Census)."
  4. G. Royle, « F102A data »
  5. (en) E. R. van Dam et W. H. Haemers, Spectral Characterizations of Some Distance-Regular Graphs. J. Algebraic Combin. 15, pages 189-202, 2003
  • Portail des mathématiques
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.