Graphe en échelle
Un graphe en échelle (en anglais : ladder graph) est, en théorie des graphes, une famille de graphes qui ont la structure d'une échelle. Un graphe en échelle se compose de deux graphes linéaires de même longueur (les montants), et deux nœuds correspondants sont reliés par une arête (les barreaux). Chaque graphe en échelle est le produit cartésien de deux graphes linéaires, dont l'un a exactement une arête ; c'est donc un graphe grille particulier.
| Graphe en échelle | |
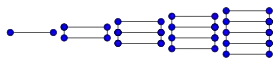 Les graphes en échelle , , , et . | |
| Notation | |
|---|---|
| Nombre de sommets | |
| Nombre d'arêtes | |
| Diamètre | |
| Nombre chromatique | 2 |
| Indice chromatique | 3 pour n > 2 n pour n = 1,2 |
| Propriétés | Distance-unité Hamiltonien Planaire Biparti |
Propriétés

Un graphe en échelle est le produit cartésien
des deux graphes linéaires et et est ainsi le graphe grille particulier .
D'autres propriétés sont :
- Les graphes en échelle sont connexes, planaires et bipartis . Pour , ils sont également cycliques et hamiltoniens.
- À l'exception des quatre nœuds d'angle de degré deux, les nœuds d'un graphe en échelle sont de degré 3.
- Le diamètre et la taille maximale d'un ensemble stable du graphe en échelle sont tous deux égaux à .
- Le nombre chromatique du graphe en échelle est 2 et son polynôme chromatique est .
- Le nombre de couplages parfaits du graphe en échelle est égal au nombre de Fibonacci [1].
Extensions cycliques
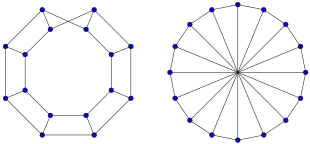
Lorsque l'on relie, dans un graphe en échelle, le premier et l'avant-dernier ainsi que le deuxième et le dernier nœud sont reliés l'un à l'autre par une arête supplémentaire, on obtient l'ensemble d'arêtes
- ,
et on obtient un graphe en échelle cyclique (anglais : circular ladder graph), noté . Un graphe en échelle cyclique est le produit cartésien d'un graphe linéaire avec un graphe cycle ; il est donc 3-régulier pour . Les graphes en échelle cycliques sont les graphes polyédriques de prismes et sont également appelés graphes prismatiques ou graphes de prisme (anglais : prism graphs).
Si les quatre nœuds sont en revanche connectés en croix, on forme l'ensemble d'arêtes
- ,
et on obtient un graphe appelé graphe en échelle de Möbius (en anglais : Möbius ladder graph), noté ; il rappelle la bande de Möbius et est également 3-régulier. Les graphes en échelle de Möbius pour ne sont plus planaires ; ils ont des propriétés intéressantes en théorie des graphes[2].
Notes et références
- (de) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en allemand intitulé « Leitergraph » (voir la liste des auteurs).
Bibliographie
- W. W. R. Ball et H. S. M. Coxeter, Mathematical Recreations and Essays, New York, Dover, , 13e éd..
- H. Hosoya et F. Harary, « On the Matching Properties of Three Fence Graphs », J. Math. Chem., vol. 12, , p. 211-218.
- M. Maheo, « Strongly Graceful Graphs », Disc. Math., vol. 29, , p. 39-46.
- M. Noy et A. Ribó, « Recursively Constructible Families of Graphs », Adv. Appl. Math., vol. 32, , p. 350-363.
- Yichao Chen, Jonathan L. Gross et Toufik Mansour, « Total Embedding Distributions of Circular Ladders », Journal of Graph Theory, vol. 74, no 1, , p. 32–57 (DOI 10.1002/jgt.21690, CiteSeerx 10.1.1.297.2183).
Article lié
Liens externes
- (en) Eric W. Weisstein, « Ladder Graph », sur MathWorld
- Portail des mathématiques
- Portail de l'informatique théorique