Graphe semi-symétrique

En théorie des graphes, un graphe non-orienté est semi-symétrique s'il est arête-transitif et régulier, mais pas sommet-transitif[1]. Autrement dit, un graphe est semi-symétrique s'il est régulier et si son groupe d'automorphismes agit transitivement sur ses arêtes, mais pas sur ses sommets.

Familles de graphes définies par leurs automorphismes
distance-transitif	→	distance-régulier	←	fortement régulier
↓
symétrique (arc-transitif)	←	t-transitif, $(t \geq 2)$		symétrique gauche (en)
↓
_{(si connexe)} sommet-transitif et arête-transitif	→	régulier et arête-transitif	→	arête-transitif
↓		↓		↓
sommet-transitif	→	régulier	→	_{(si biparti)} birégulier
↑
graphe de Cayley	←	zéro-symétrique		asymétrique

Propriétés

Tout graphe semi-symétrique est biparti[2], et son groupe d'automorphisme agit transitivement sur les deux sous-ensembles de sommets de la bipartition[3].

Il n'existe aucun graphe semi-symétrique d'ordre 2p ou 2p², où p est un nombre premier[4].

Exemples

Le plus petit graphe semi-symétrique est le graphe de Folkman, qui possède 20 sommets[3].

Tous les graphes cubiques semi-symétriques d'ordre inférieur à 768 sont connus[5]. Le plus petit d'entre eux est le graphe de Gray, qui possède 54 sommets[6].

Graphe de Folkman, plus petit graphe semi-symétrique, à 20 sommets.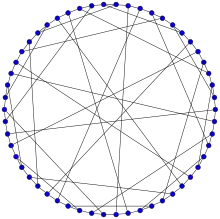
Graphe de Gray, plus petit graphe cubique semi-symétrique, à 54 sommets.
Graphe de Ljubljana, graphe cubique semi-symétrique à 112 sommets.
12-cage de Tutte, graphe cubique semi-symétrique à 126 sommets.

Notes et références

(en) Dragan Marušič et Primož Potočnik, « Semisymmetry of Generalized Folkman Graphs », European Journal of Combinatorics, vol. 22, n^o 3,‎ 1^er mars 2001, p. 333–349 (ISSN 0195-6698, DOI 10.1006/eujc.2000.0473, lire en ligne, consulté le 3 juillet 2019)
(en) Norman Biggs, Algebraic Graph Theory, 2^d Edition, Cambridge University Press, 1993, 214 p. (ISBN 978-0-521-45897-9, lire en ligne), p. 115-116
(en) Eric W. Weisstein, « Semisymmetric Graph », sur mathworld.wolfram.com (consulté le 3 juillet 2019)
(en) Jon Folkman, « Regular line-symmetric graphs », Journal of Combinatorial Theory, vol. 3, n^o 3,‎ 1^er octobre 1967, p. 215–232 (ISSN 0021-9800, DOI 10.1016/S0021-9800(67)80069-3, lire en ligne, consulté le 3 juillet 2019)
(en) Marston Conder, Aleksander Malnič, Dragan Marušič et Primž Potočnik, « A census of semisymmetric cubic graphs on up to 768 vertices », Journal of Algebraic Combinatorics, vol. 23, n^o 3,‎ 1^er mai 2006, p. 255–294 (ISSN 1572-9192, DOI 10.1007/s10801-006-7397-3, lire en ligne, consulté le 3 juillet 2019)
(en) Dragan Marušič, Tomaž Pisanski et Steve Wilson, « The genus of the GRAY graph is 7 », European Journal of Combinatorics, topological Graph Theory and Graph Minors, second issue, vol. 26, n^o 3,‎ 1^er avril 2005, p. 377–385 (ISSN 0195-6698, DOI 10.1016/j.ejc.2004.01.015, lire en ligne, consulté le 2 juillet 2019)

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) Dragan Marušič et Primož Potočnik, « Semisymmetry of Generalized Folkman Graphs », European Journal of Combinatorics, vol. 22, n^o 3,‎ 1^er mars 2001, p. 333–349 (ISSN 0195-6698, DOI 10.1006/eujc.2000.0473, lire en ligne, consulté le 3 juillet 2019)

[:0-2] (en) Norman Biggs, Algebraic Graph Theory, 2^d Edition, Cambridge University Press, 1993, 214 p. (ISBN 978-0-521-45897-9, lire en ligne), p. 115-116

[:1-3] (en) Eric W. Weisstein, « Semisymmetric Graph », sur mathworld.wolfram.com (consulté le 3 juillet 2019)

[4] (en) Jon Folkman, « Regular line-symmetric graphs », Journal of Combinatorial Theory, vol. 3, n^o 3,‎ 1^er octobre 1967, p. 215–232 (ISSN 0021-9800, DOI 10.1016/S0021-9800(67)80069-3, lire en ligne, consulté le 3 juillet 2019)

[5] (en) Marston Conder, Aleksander Malnič, Dragan Marušič et Primž Potočnik, « A census of semisymmetric cubic graphs on up to 768 vertices », Journal of Algebraic Combinatorics, vol. 23, n^o 3,‎ 1^er mai 2006, p. 255–294 (ISSN 1572-9192, DOI 10.1007/s10801-006-7397-3, lire en ligne, consulté le 3 juillet 2019)

[6] (en) Dragan Marušič, Tomaž Pisanski et Steve Wilson, « The genus of the GRAY graph is 7 », European Journal of Combinatorics, topological Graph Theory and Graph Minors, second issue, vol. 26, n^o 3,‎ 1^er avril 2005, p. 377–385 (ISSN 0195-6698, DOI 10.1016/j.ejc.2004.01.015, lire en ligne, consulté le 2 juillet 2019)